从零开始学算法：7.跳表

在公众号中回复“ACM模板”你将免费获得我大学耗时四年整理的《ACM算法模板》。
如果大家想加入我的星球，可以加我微信，我免费给你拉进去，加我时暗号”算法星球”。

一、背景

大家好，我是tiankonguse。
由于某些原因，经常有人想学习算法但之前又没有相关经验，不知道从何做起。
我思考了许久，计划写一个系列来分享如何入门学习算法。

之前已经分享了《认识算法》、《了解套路长啥样》、《排序算法》、《二分查找》、《链表》，这是第七篇《跳表》。

一、基础知识

在上一篇文章《链表》最后我们通过分块把复杂度降到了O(sqrt(n))，还提到有一个方法可以做到O(log(n))的插入或删除复杂度。
这个数据结构就是跳表。

写完这篇文章时，发现一个重大秘密：跳表其实与顺序没有关系的，也就是跳表可以无序的。
业界都是用于维护有序序列，实际情况是跳表完全可以用于操作随机序列。
原来跳表才是一个真实的万能数组了，各种复杂度都可以接受，REDIS的LIST看来要重写了。
不过这里我们先以有序序列为例来讲解跳表，对于无序的，只需要忽略比大小操作就行了。

对于跳表是啥，其实不好描述，但是看图模拟操作一下，应该就可以马上明白他的原理了。

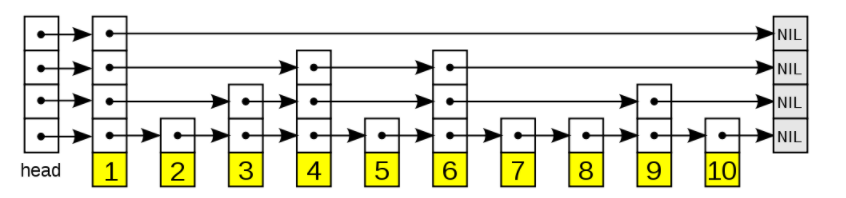
（图片来自维基百科）

首先可以看出来，我们有一个数组链表头，长度固定，并且表头的每个位置都是一个指针，指向后面。
对于每个位置，同样也有一个数组链表头，有不定的高度以及值信息，结构如下.

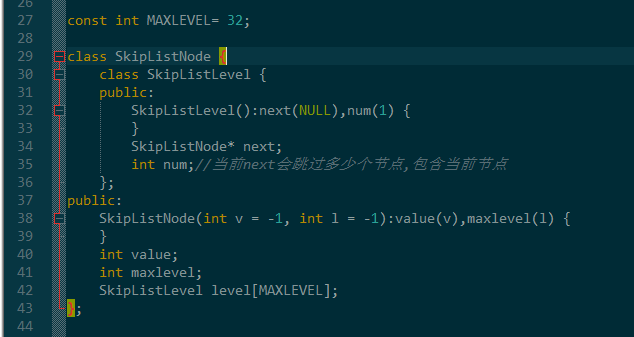
二、查找

看一个数据结构如何设计的，最简单的方式就是看查找的实现了。

跳表的查找步骤如下：
0.定义左边界为head
1.左边界从上到下依次遍历表头
2.发现是NULL代表当前层数没找到，层数下移
3.如果不是NULL，所在位置我们称为A，A对应的值和查找的值比大小
4.查找的值小于A，说明答案在A左边，从下一层数继续查找。
5.查找的值大于等于A，说明答案在右边，左边界更新为A，从当前层数继续查找（重点注意）。
6.如果遍历到最后一层了，还没找到，说明不存在。

可能看着上面的描述步骤太抽象，那我们举个具体的例子吧。

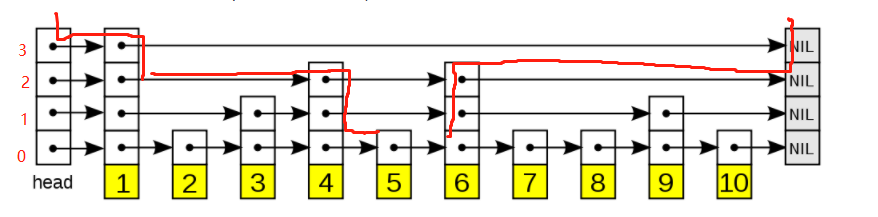
这里以查找5为例。
0.左边界为head，总共有4层，当前层数3
1.位置（head, 3）从第3层开始，遇到节点1，比较5大于1，左边界置为1
2.位置（1, 3）从第3层开始，遇到nul，层数下降
3.位置（1, 2）从第2层开始，遇到节点4，比较5大于等于4，左边界置为4
4.位置（4, 2）从第2层开始，遇到节点6，比较5小于6，层数下降
5.位置（4, 1）从第1层开始，遇到节点6，比较5小于6，层数下降
6.位置（4, 0）从第0层开始，遇到节点5，比较5大于等于5，左边界置为5
7.位置（5, 0）从第0层开始，遇到节点6，比较5小于6，层数下降
8.位置（5, -1）结束了

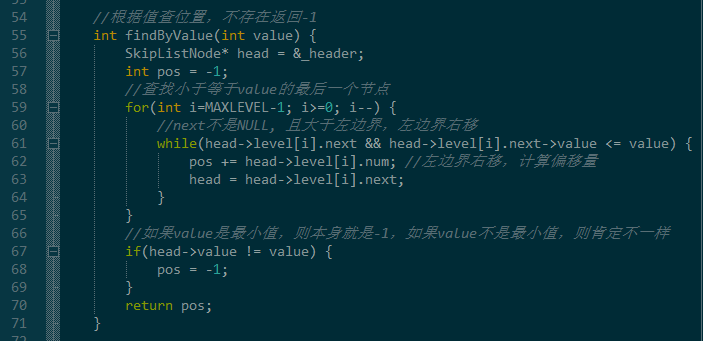
上面步骤的实现代码如下，可以发现，非常简单。
里面多了一个num, 用于计算偏移量，这样就可以知道查找值得坐标了。

三、插入

我们查找的时候，知道了节点的关键信息有三个：节点值、节点每层到下层的指针和距离。
现在我们需要在指定的位置插入一个值了，必然需要更新MAXLEVEL个链表，以及更新2*MAXLEVEL个链表间的距离。

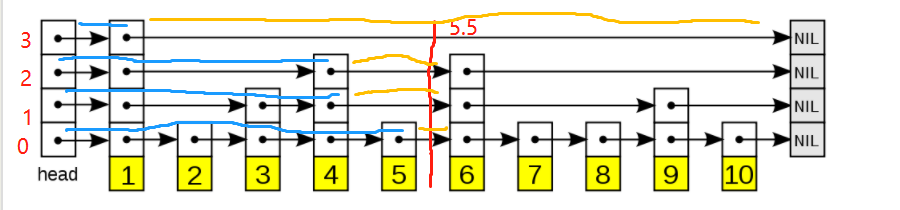
如上图，假设我们要插入 5.5。
棕黄色的含义是当前节点到下个节点之间的节点个数，也就是我们储存的num字段。
浅蓝色的含义是当前位置之前有多少个节点，我们命名为preNum。
各层的蓝色线终点和preNum都可以在查找5.5的时候计算出来。
这样，我们插入5.5的时候，5.5的各层num与各层链表之前的num都可以通过简单的数学运算计算出来。

比如第3层前半段链表的num = 第0层的preNum（最长的蓝线）- 第三层的preNum（最短的蓝线） + 1.
而对于第三层后半段链表的num = 第三层的num(最长的黄线) - 第3层前半段链表的num(上面计算的值)

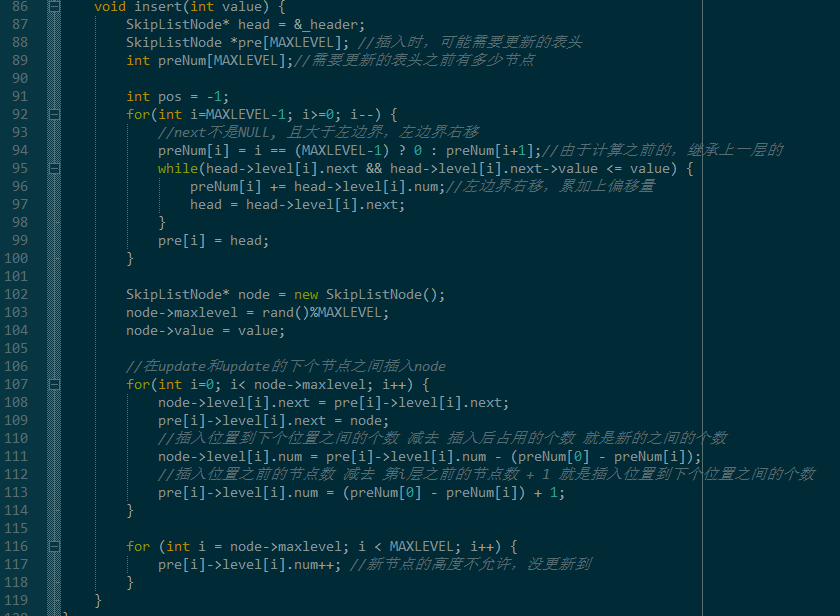
上面描述对应的代码就是下面这个函数，实现也不复杂。
有个地方需要说明一下，新插入的节点的高度是随机计算的，这样做的风险可能会导致这个算法退化为O(n)的复杂度。

四、删除

删除和插入是相反的操作，而且更简单。
找到位置后，直接把删除位置的num加到之前的节点，然后删除聊表即可。
这里就不多说了。

五、下标定位

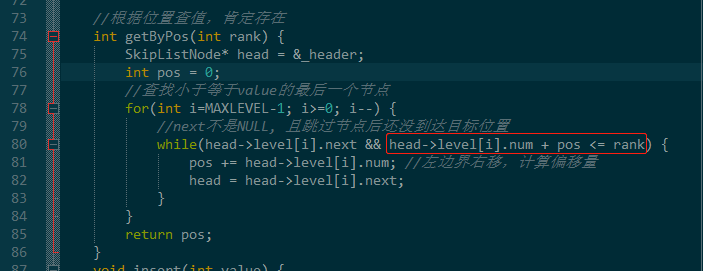
由于储存了每个位置每层到下个next之间的节点数，这里就可以快速的判断是否可以跳过下个next。
跳过了更新总偏移量，没跳过则进入下一层，代码如下。

六、最后

知道了跳表节点储存的信息：值、各层到下个节点的指针和距离，我们就可以轻松的实现跳表了。
如果你没看明白，不要紧，多看几遍查找的步骤，你应该就能明白跳表的实现原理。

对于跳表，是个有序的序列，我们可以Log(n)的复杂度插入或删除一个数据，也可以在log(n)的复杂度内通过下标定位到对应的位置。

文章的开头说了，我们并不需要跳表有序。
我们只使用下标来增加数据或删除数据的话，跳表就是一个强大的数组了，而且平均复杂度也是O(n)的。

那为啥大家分享的跳表都是有序的呢？
第一个原因是无序的跳表意义不大，实现难度相比数组高出几个数量级，真要使用无序的了还不如使用其他的代替数据结构。
更关键的原因是业界都是使用跳表来实现有序集，从而做到快速查询。
比如redis、levelDB等开源软件都实现了有序跳表。

这样想来，无序跳表活得好憋屈，google了一下，竟然没有人使用这个方法。
redis如果使用跳表优化一下list一下的话，复杂度就可以从O(n)的复杂度提升到O(log(n))了。
震惊，我发现了一个log(n)的list数据结构，有序跳表，哈哈。

本文首发于公众号：天空的代码世界，微信号：tiankonguse-code。