Leetcode 第139场比赛回顾

零、背景

Leetcode 第139 场比赛的题目难度属于中等难度。
只可惜我的思维还是太慢，敲代码速度太慢，浪费不少时间。
最后一道题就差几分钟就敲完代码了，但是比赛结束了，然后以提交，就过了。

接下来就看看看这四道题吧。

一、字符串的最大公因子

题意：问是否存在一个子串，是输入两个串的重复子串（无交集）。

思路： 这道题直接暴力从大到小枚举判断即可。
但是我犯了算法洁癖症，想着最优解，浪费不少时间。

比如我的方法是：
第一步：对两个串的长度求 GCD，答案肯定小于等于GCD。
第二步：枚举所有小于GCD的数字，判断是否分别是两个串的重复子串。

而且在判断是不是重复子串时，可以使用 MOD 来快速判断（是的话需要能够 %MOD = 0）。

中间代码敲了一半时，我甚至想也许还可以用二分。
最后一看时间已经过了 15 分钟了，赶紧清空代码写了一个暴力算法把题过了。

二、按列翻转得到最大值等行数

题意：给一个0/1矩阵，可以翻转一些列，使得一些行的值全部相等。求最大的相等行数。

思路：可以发现，最终相等的行的值要么全是0，要么全是1。

对于全是 0 的行，例如 line[i]和line[j]，翻转某些列后，这些行依旧是相等的，即 line[i] = line[j] 。
对于全是 1 的行，同理，不管怎么翻转，这些行组成的数组都是相同数组。
对于 0 与 1 的行，最终每个位置应该都是相反的，那翻转列之前，每个位置也应该是相反的。

因此我们可以假设第 i 行是最终答案，然后统计和第 i 行完全相等以及完全相反的行数，然后求最大值。

这里我又犯了洁癖症，标准的方法是暴力做，复杂度是 O(n^2*m) 。
我的做法是预处理，对每一行数据序列化为字符串，然后使用 map 计数与查找，复杂度优化到了 O(n*m) ，只是我的时间都浪费了。

三、负二进制数相加

题意：给两个以-2为基数的数字，求两个数字之和。

思路：对于大整数加法，是有套路的。

第一步是翻转字符串，使得低位在前面，高位在后面。
第二步是高位补零。
第三步是相加。由于-2基数的特殊性，这里我们暂时不管进位问题。
第四步是处理进位逻辑。
第五步去前导零。
第六步翻转结果，即得到答案。

这里最关键的一步是如何处理进位。
如果当前位的值是0和1，那就不需要处理。
如果当前位大于等于2，且下一位大于0，那么可以抵消，即2*(-2)^k + (-2)^(k+1) = 0。
如果当前位是2且下一位为0，则可以转化为后面两位的运算结果，即2 * (-2)^k = (-2)^(k+1) + (-2)^(k+2) 。

证明：
当k是偶数时，最终结果是2^(k+1)，那公式展开-2^(k+1) + 2^(k+2) = 2^(k+1)。
当k是奇数时，最终结果是-2^(k+1)，那公式展开2^(k+1) - 2^(k+2) = -2^(k+1)。

由此，则可以完美的处理所有的进位了。

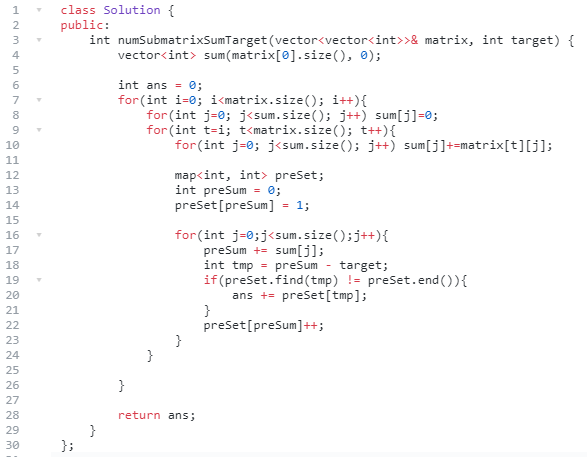
四、元素和为目标值的子矩阵数量

题意：给一个矩阵，问满足要求的子矩阵个数。
这里的要求是矩阵和等于给定的值。

思路：对于子矩阵问题，有一个万能的方法。
首先是枚举子矩阵的上面那条边，然后枚举矩阵的下面那条边，这个过程中，可以累积计算出每一列的值，目前复杂度O(n^2)。
这样，问题就转化为了有一个一维数组（列的累计值），求这个数组里面满足要求的子数组个数。

对于一维数组求子数组最优值，则需要具体情况具体分析了，但是复杂度不要超过O(n^2)，最优的是O(n)，次之是O(n log(n))。

比如对于最大子矩阵和，就可以转化为最大子序列和，就是O(n)的复杂度算出最大序列和，综合就是O(n^3)。

这道题是求子序列和等于指定值的个数，那就只能统计前缀和O(n)，然后判断快速判断当前后缀是否存在答案了O(log(n))。

具体来说，如果当前位置now为后缀的子序列pre+1,...,now是一个答案，则说明当前前缀1,2,3,..., now和减去前面的某个前缀和1,2,...,pre 等于指定值。
反过来就是，当前前缀1,2,3,..., now减去指定值，存在某个1,2,...,pre 等于这个差值。

、 这里使用map或者hash_map储存前缀和以及个数，然后查找差值是否存在，存在则找到一个答案。

五、最后

回头看看，这次比赛题挺好的，难度适中，大家花一些时间思考一下，做出三道题应该是没问题的。

四道题解在 leetcode 上我也分享了，刷题的朋友可以帮我点个赞，虽然我不知道 leetcode 上点赞有啥用。

地址：https://leetcode.com/tiankonguse/

-EOF-