2020 腾讯程序设计竞赛（一）

一、背景

这周某天晚上参加了腾讯举办的2020 TPC 程序设计竞赛第一场比赛。

比赛时间其实非常不好。

比赛前半小时还没吃饭，还在开会。
开完会赶紧吃饭，然后找个没人的地方准备环境。
当时去厕所以及去回收桶扔饭盒都是小跑，可见时间有多紧凑。

不过还好，比赛前5分钟打开了电脑，终于可以比赛了。

最终被虐，只做出一道题。
赛后进行复盘，发现努力一下有可能做出三道题。

不过想想，人生一大错觉就是这道题我能做出来。
下次目标定位做两道题吧。

一、整数分组

题意：对 1~n 数字进行分组，使得每个分组内的数字两两互质。
求最小分组个数。

解释：分组内两两互质就是任意两个数字都需要互质。

思考：第一眼看到这道题就懵逼了，完全不会呀。

然后一想，隔一个就有一个偶数，那至少需要 n/2 个分组。

其他的数字是不是可以放进这 n/2 的数组里面且互质呢？

纸上画出了前20个数字，发现确实可以。

于是答案就确定了，max(n/2, 1) 即可。

二、递归翻硬币游戏

题意：如上图，给一个 flip 函数。
然后给两个 01 字符串，问第一个字符串能否 主动调用 flip 函数反转为第二个字符串。
如果可以输出最少的主动调用次数。

解释：题意要求的是主动调用次数，调用一次后，递归的不算。

经过：起初我看错题意了，没看到递归调用。
我把题意理解为开关灯了，只会影响左右两个位置。

代码敲完后，样例都没过，最终放弃这道题。
赛后一分钟重新读了题，理解之后几分钟就写出了代码。

思路：第一步理解 flip 函数。
由于递归的存在，flip 函数相当于使连续一片区间相同的硬币全部反转，直到左右不反转也是相同的。

根据函数的含义，可以得到第一个的结论：区间不可拆分。

假设目标存在相邻位置值不同的情况，那原始输入也需要是不同的。

比如目标存在一个相邻位置是01， 原始输入相同位置是00或者11。
00是无论如何也不能反转为01的，即区间不可拆分。

另外，假设目标是01，如果输入是10会怎么样呢？
我们可以发现，10也是无法反转为01的。

所以我们可以检查所有相邻位置不同的地方，只要有一个不一致，那就没答案。

如果上面检查过了，剩下的片段肯定都是下面的样子。

目标值111111，输入值1xxxx1。
或者目标值000000，输入值0xxxx0。
即目标片段全部相同，输入片段左右与目标相同，中间可能不同。

假设一个片段分为 n 组连续区间。
比如1100110011 有 5 个连续区间。
其中有 n/2 个需要反转的区间，所以需要反转 n/2 次才能使区间连续。

所以我们只需要找到所有片段，统计区间，除2求和即可。

三、九宫谜题

题意：给一个 3*3 的九宫格，填入数字 1~9。
有两种操作可以选择：
1、选择一行，向右旋转。
2、选择一列，向下旋转。

问能够从一个九宫格转到另外一个九宫格。
如果可以，给出最小操作次数。

思路：刚开始我直接搜索，结果超时了。

突发奇想，既然存在不可能状态，那可能的状态是不是有限的呢？

于是打印了一下总个数，发现一个状态可能到达十几万个状态，最多13层。
所以第一个方法是预先计算出所有状态的答案，打表接口。

我打表的时候电脑跑了好几秒，怕会超时。
便继续分析状态间的关系。

每个状态可以转移到其他6个状态，总共十几万个状态，状态之间是完全对称的。

由此可以想象，所有状态组成了一个完美对称的网状图，可以画出一个非常完美的圆或者球来。

既然这样，我们可以双向搜索，这样状态将会大大的减少。
我跑了7层，发现只有几千个状态，那双向搜索就可以搜索几千次就确认是否有答案。

双向搜索大概像下面的圆，最坏情况是从两个最远点出发，搜索的路径形成扇形。
阴影部分是搜索区域，其他区域是不需要搜索的区域。

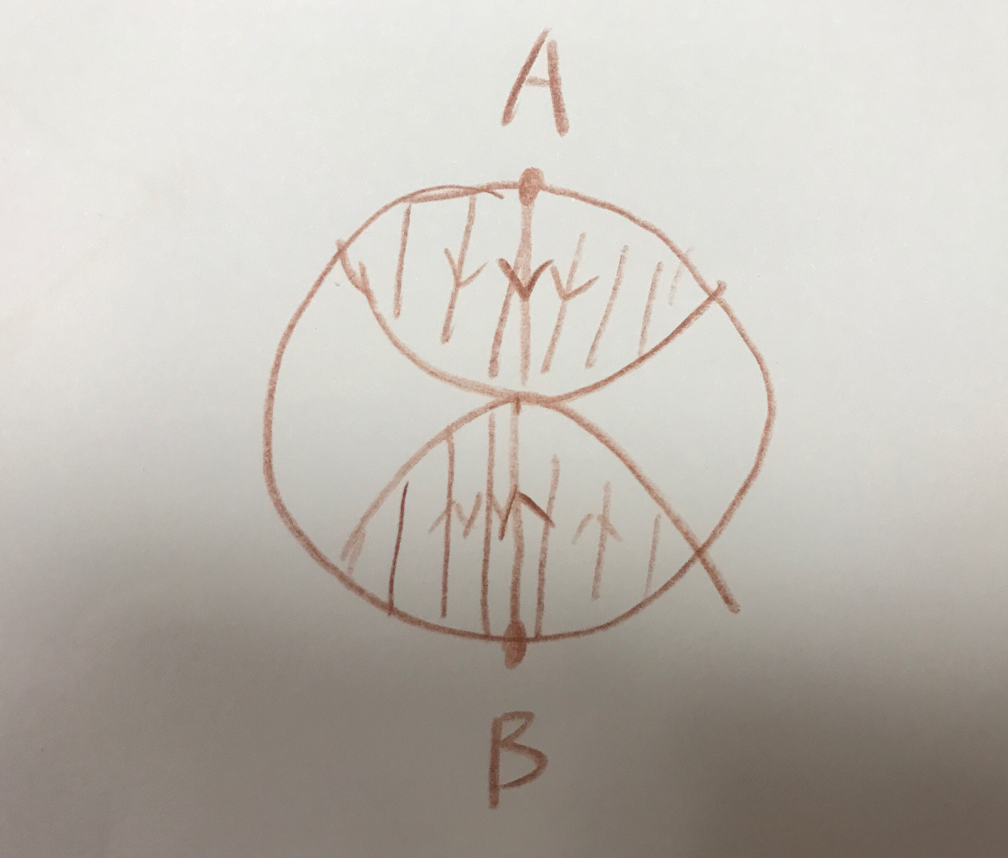
赛后一看题解，只能打表做。

有T组测试样例，打表的话复杂度是 O(T+ 20W)。
双向搜索的话复杂度是 O(5000 * T)。
双向搜索还是会超时的。

四、三进制字符串计数

题意：长度为m的三进制共有3^m个。
如果长度为m的所有子串都是字符串s的子序列，则称 s-m 完美。

现在给一个三进制字符串，其中有些位置是?，问可以组成多少个不同的 s-m 完美。

思路：显然是动态规划题。

题意转化一下，就是有 k 个问号，即有 3^k个不同的三进制字符串，问其中有多少个满足 s-m 完美。

转化后还是没思路，不会做，放弃。

五、最后

这次比赛第一题算是找规律了，第二题也是找规律，第三题是搜索题。

其中第三题最有意思了，很多人使用双向搜索提交了，也超时了。

我很早就打表了，但我打表的目的是为了计算双向搜索的复杂度，而潜意识的认为打表会超时。
果然思维还是转的不够快，没想到来对比下复杂度。

这时候分析下复杂度的话，就会发现打表的总复杂度比搜索的复杂度更低。

果然自己还是太菜，在众多的选择中，没能选中最优解，还需要继续多多练习吧。

《完》

-EOF-

本文公众号：天空的代码世界
个人微信号：tiankonguse
公众号ID：tiankonguse-code