leetcode 第 215 场算法比赛

零、背景

这次比赛有点事，没有参加。

赛后找时间做了一下，发现这次比赛的最后一题很有意思，涉及到一个新的知识点：轮廓线动态规划。

到最后一题的时候，我们再来细看这个算法吧。

一、设计有序流

题意：给一个输入流，不断的插入到队列中。 然后有一个游标，默认值是 1。
如果输入一次后，当前游标的值存在，则输出游标之后连续递增的所有流数据。
此时游标的值更新为输出的最大值加一。

思路：按照题意模拟即可。

源代码： https://github.com/tiankonguse/leetcode-solutions/blob/master/problemset-new/016/01656-design-an-ordered-stream/design-an-ordered-stream.cc

二、确定两个字符串是否接近。

题意：给两个字符串，可以按下面的规则对一个字符串进行转换。

1）交换任意两个位置的字符。
2）交换任意两个字母。

思路：

第一个转化可以确定字符串与顺序无关，只需要统计每个字母的个数。
第二个转化可以确定字母出现的个数排序后需要匹配。

根据这两个结论，对字母统计个数，在对个数进行统计次数即可。

注意实现：两个字符串出现的字母集合需要一致。

源代码： https://github.com/tiankonguse/leetcode-solutions/blob/master/problemset-new/016/01657-determine-if-two-strings-are-close/determine-if-two-strings-are-close.cc

三、将 x 减到 0 的最小操作数。

题意：给一个正整数组成的数组，问是否存在一个前缀和后缀，使得前缀与后缀之和等于指定值 x。
如果存在，输出前缀和后缀长度和的最小长度。不存在则输出 -1。

思路：

第一个方法是统计所有后缀和的最小长度，然后枚举前缀，判断是否存在满足要求的后缀。
复杂度: O(n)。

代码： https://github.com/tiankonguse/leetcode-solutions/blob/master/problemset-new/016/01658-minimum-operations-to-reduce-x-to-zero/minimum-operations-to-reduce-x-to-zero.cc

第二个方法是逆向思维。
题意是查找前缀和后缀的最小长度，可以转化为查找中缀的最大长度。

由于数组都是正整数，可以使用滑动窗口来计算。

代码： https://github.com/tiankonguse/leetcode-solutions/blob/master/problemset-new/016/01658-minimum-operations-to-reduce-x-to-zero/minimum-operations-to-reduce-x-to-zero-sliding-window.cc

四、最大化网格幸福感。

题意：给一个n*m的网格，以及黑白两种颜色的球，每个网格可以放一个球。

放球的时候存在四种分数计算规则：

1）白球自身可以得 120 分。
2）黑球自身可以得 40 分。
3）白球周围每存在一个其他球，就扣 30 分。
4）黑球周围每存在一个其他球，就加 20 分。

问该如何放球，使得得分最高（球可以不放完）。

思路：

首先看数据范围，矩阵大小最大是5*5，白球和黑球都不超过 6 个。

看到数据范围很小，可以想到使用状态压缩来做这道题。

每一个方格有三种状态：不放球、放黑球、放白球。
假设每行有 m 个方格，则每行有3^m个状态。

定义状态f(n, a, b, k) 代表前 n 行可以放 a 个白球、b 个黑球，最后一行状态是 k 时的最优答案。
则这个状态可以使用 3^m 个子状态计算得到。
复杂度：n * a * b * 3^m * 3^m

由于合并子状态的过程中还有一个O(m)的计算，如果直接写这个状态压缩的话，可能会超时。
可以提前把各种计算逻辑预处理计算出来。

之后就可以勉强通过这道题了。

源代码： https://github.com/tiankonguse/leetcode-solutions/blob/master/problemset-new/016/01659-maximize-grid-happiness/maximize-grid-happiness.cc

其实，对于矩阵上的状态压缩，还有一个高阶方法，叫做扫描线状态压缩或者轮廓线状态压缩。

如下图，只需要储存浅绿色的状态即可。

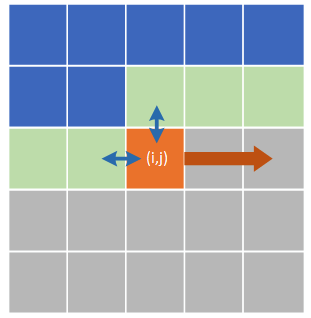
此时，定义状态f(p,a,b,k) 代表前 p 个数字放 a 个白球、b 个黑球，且最后 m 个状态是 k 的最优答案。
这个状态可以使用3个子状态计算得到。
复杂度：n*m * a * b * 3^m

可以发现，与普通的状态压缩相比，复杂度从O(3^m)将到了O(m)。

源代码： https://github.com/tiankonguse/leetcode-solutions/blob/master/problemset-new/016/01659-maximize-grid-happiness/maximize-grid-happiness-outline.cc

五、最后。

这次比赛的最后一题有点难度，普通的状态压缩可能超时，轮廓线状态压缩很多人没听说过。
不过这次做了这道题，应该就听说过了，下次应该就会做了。

加油，算法人。

《完》

-EOF-

本文公众号：天空的代码世界
个人微信号：tiankonguse
公众号ID：tiankonguse-code