【算法】栈理论就是这么简单

一、背景

之前写了五篇文章来讲解了《数组就是这么简单》系列，昨天写了一篇文章来讲解《队列就是这么简单》，今天用一篇文章来介绍《栈就是这么简单》吧。

二、栈的定义

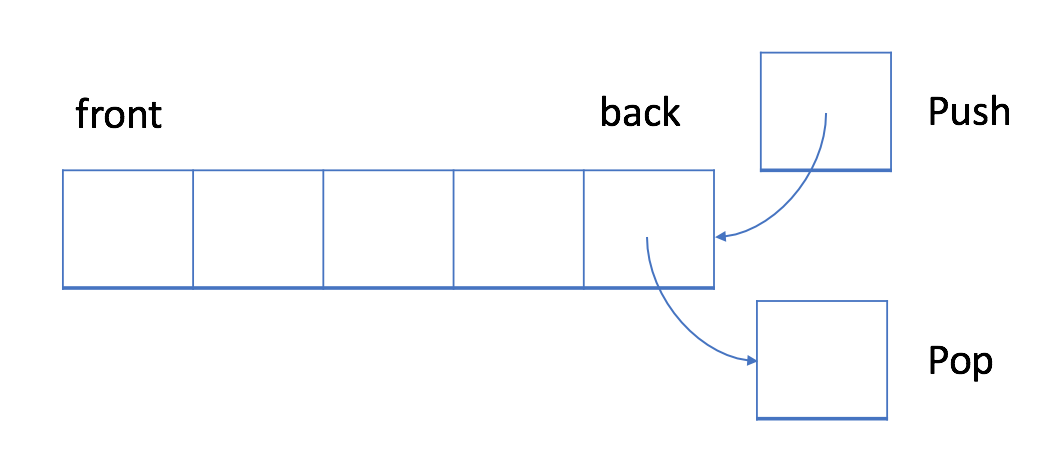
队列是一种LIFO的数据结构。
LIFO全称是Last In First Out，即后进先出的意思。
内置的操作有：入栈(push)、出栈(pop)、是否为空(empty)、栈顶(top)，大小(size)等。

使用数组实现的话，代码大概如下：

class MyStack {
    private:
        vector<int> data;
    public:
        void push(int x) {
            data.push_back(x);
        }
        void pop() {
            data.pop_back();
        }
        bool empty() {
            return data.empty();
        }
        int top() {
            return data.back();
        }
        int size(){
            return data.size();
        }
};

下面我们来看看栈的一些初级应用吧。

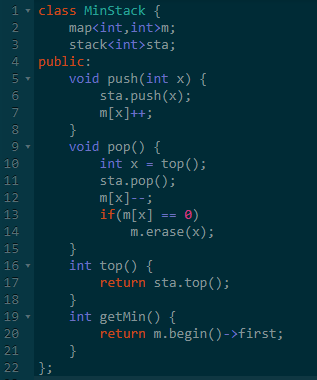
三、最小栈

题意：实现一个最小栈，包含push、pop、top、getMin 四个功能。

思路：如果没有getMin这个功能，上一小节的代码就可以满足题意。
但是有一个查找最小值，这里就需要考虑怎么实现了。

如果暴力实现，则是每次查询最小值时，遍历整个数组。复杂度O(n)。
如果我们提前使用某种数据结构储存起来的话，就可以做到快速查询。

这里我们利用map的key是有序的特点来在O(log(n))的时间内找到最小值。
当然，代价是入栈和出栈时也要使用O(log(n))的复杂度来更新这个数据结构。

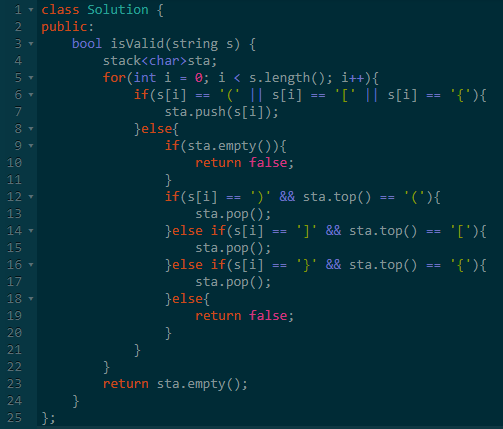
四、有效的括号

题意：给一个括号组成的字符串，判断括号是否匹配。
这是学习栈的经典例子。

思路：扫描到位置k的时候，我们假设前面匹配的括号我们已经删除了，尚未匹配的字符我们储存在某种数据结构中了（肯定都是左括号）。
第k个字符如果是左括号，我们需要将这个左括号放进数据结构中。
而第k个字符如果是右括号，则数据结构里面，最后放进去的那个字符肯定和第k个括号匹配。否则这个字符串就是不匹配的。
匹配时，还需要从数据结构里删除最后进去的那个字符。
当扫描结束时，如果字符串是匹配的，我们的数据结构应该恰好也为空。

代码如下：

五、每日温度

题意：告诉你每天的温度，需要计算每天需要等几天才会高于当天的温度。

思路：这道题使用数学术语表示，就是在数组里，求每个数字之后第一个大于当前数字的距离。

第一个方法当然是暴力方案，即每个数字都循环一遍去计算答案。复杂度O(n^2)。

第二个方法就需要观察这个问题的特征了。
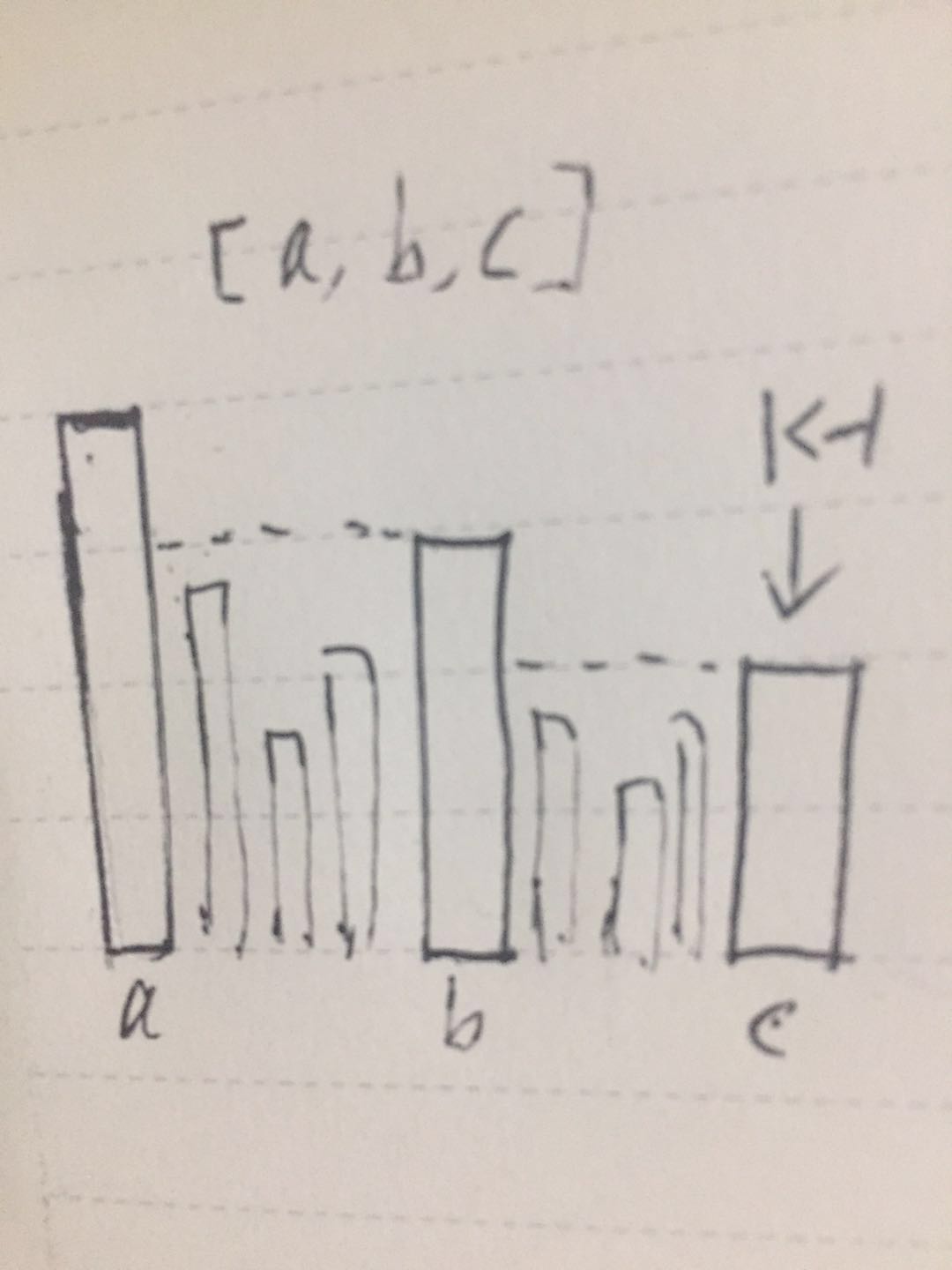
假设我们扫描到位置k时，前面的数据分两部分：一部分是已经知道答案的，一部分是不知道答案的。

先看不知道答案的数据有什么特征。
对于k-1位置的数字，我们肯定不知道答案，因为是最后一天。
倒数第二个不知道答案的位置假设是p，则p的值肯定大于k-1的值，而且p+1 ~ k-1之间的数字都不大于k-1。
倒数第三个不知道答案的位置与p的关系已经如此。
这样总结一下，就可以得出尚未不知道答案的数字是一个递减序列，且序列之间的数字都小于后面那个数字。

如下图：

对于当前位置k，肯定是要入队的，但是入队前我们需要更新数据结构，使其满足递减的特征。
如果k的值大于数据结构里面的最后一个元素，则那个元素就找到答案，即答案是位置k。
这样不断操作只到不满足或者数据节后为空。
如果k的值小于等于数据结构里最后一个元素，则进入数据结构也满足递减的特征，正常进入即可。

由于我们每次都是操作数据结构最后一个元素，所以这种数据结构可以使用栈来代替。

六、逆波兰表达式求值

题意：给一个逆波兰表达式，求对应的答案。

比如有一个操作符op1和两个变量E1和E2，使用正常的中缀表达法就是 E1 op1 E2。
但是当E1或E2是另外一个表达式时，我们就需要加括号来区分计算的优先级了。
例如E1 = E3 op2 E4时，完整的表达式将是 (E3 op2 E4) op E2。

而逆波兰表达式是后缀表达法，这种定义可以做到不使用括号且明确各个公式的优先级。
比如还是上面的式子，第一个可以表达为E1 E2 op1，第二个可以表达为E3 E4 op2 E2 op1。
而当E4 = E5 E6 op3时，式子又可以展开为E3 E5 E6 op3 op2 E2 op1。

现在就是给了这样一个后缀表达式，让我们计算出表达式的值。

思路：我们可以确定遇到一个操作符时，前面肯定可以计算出两个数字供这个操作符来运算。
但是那两个数字怎么来我们就不容易看出来了。

但是我们从前往后看，可以看到一个连续的数字，然后是一个操作符。
此时这个操作符的运算是可以确定的，参与运算后，连续数字的最后连个数字会被使用删除，同时运算结果这个数字也会加进来。
这样前面的就又是一片连续的数字了，直到遇到下个运算符，然后再次参与到上面的计算逻辑中。

这里我们需要一种数据结构，来储存前面的连续数字。
考虑到每次只会操作连续数字的最后两个数字，我们可以使用栈来储存。
每次遇到数字，就入栈。
当遇到操作符，就出栈两个数字，参与计算后，结果再入栈。
如果表达式正确，计算完毕后，栈里面就只剩一个数字，即答案。

具体代码如下：

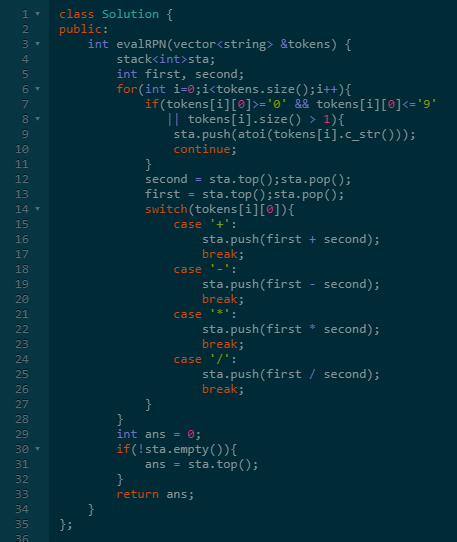
七、最后

这篇文章主要介绍了栈的基础理论，以及基本的应用。
比如自己实现栈、括号匹配、逆波兰表达式等。

简单的观察就可以发现，这些问题之所以可以使用栈，是因为这些问题提取特征后，变成了只关注最后面的数据。
即只关注最后进入数据结构的数据，这样就满足了后进先出的特征，从而可以使用栈来做。

这里面有一个因果关系需要解释一下。

我们选择栈的原因是问题的特征和栈的特征吻合，从而被选择。
而不是我们选择栈，然后发现问题的特征。

面对任何问题其实都是这样的。
先观察问题的特征，然后找现有的数据结构去匹配，如果没有就自己使用多种数据结构组合使用，来满足问题特征的操作要求。
此时，我们实际上就是构造出了一个新的数据结构，不过我们没有使用类封装起来罢了。

这里使用栈来讲这个道理大家可能认为太简单了。

其实对于其他数据结构或算法，比如动态规划(DP)、二分优化也是这样的道理。
我们通过一系列的特征推理出了一个算法和数据结构，而不是启发式的想到一个算法，然后做出这道题。

千万不要把因果关系弄反了。

毕竟启发式算法并不是可以随时能够想到，但是根据特征推理出的算法任何有逻辑与理性的人还是可以构造出来的。

PS：这篇文章简单的介绍了栈的应用，下篇文章继续来介绍栈的高级用法。

-EOF-