必备算法模版之树状数组

一、背景

之前我分享 leetcode 算法比赛题解的时候，经常会提到这个题裸用树状数组就过了，那个题裸用线段树就过了。

那怎么裸用呢？
现场根据自己的硬实力敲一个树状数组或者线段树吗？

不是的。
这些固定的算法都有固定的代码，没必要重复敲一遍。
直接从代码库里复制过来就行了。

这里的代码库我们称为模版。

今天给大家分享一个树状数组的模版库。

二、树状数组解决什么问题

先来看一个问题。

假设这里有一个数组，有两个操作。

1）修改某个位置的值。
2）求某个区间和。

正常情况下，修改的复杂度是O(1)，查询的复杂度是O(n)。
如果有 m 个操作，那总复杂度就是 O(nm)了。

而通过树状数组，修改和查询的复杂度都是O(log(n))。
这样总复杂度就是O(m log(n))了。

所以树状数组主要用来解决单点更新、前缀查询的问题。
而两个前缀和求差就是区间和，所以也可以解决区间问题。

三、树状数组的原理

树状数组的本质是分治法，即将问题拆分为若干个字问题逐个解决，最后合并得到答案。

具体原理上，按照 bit 位拆分子问题的。

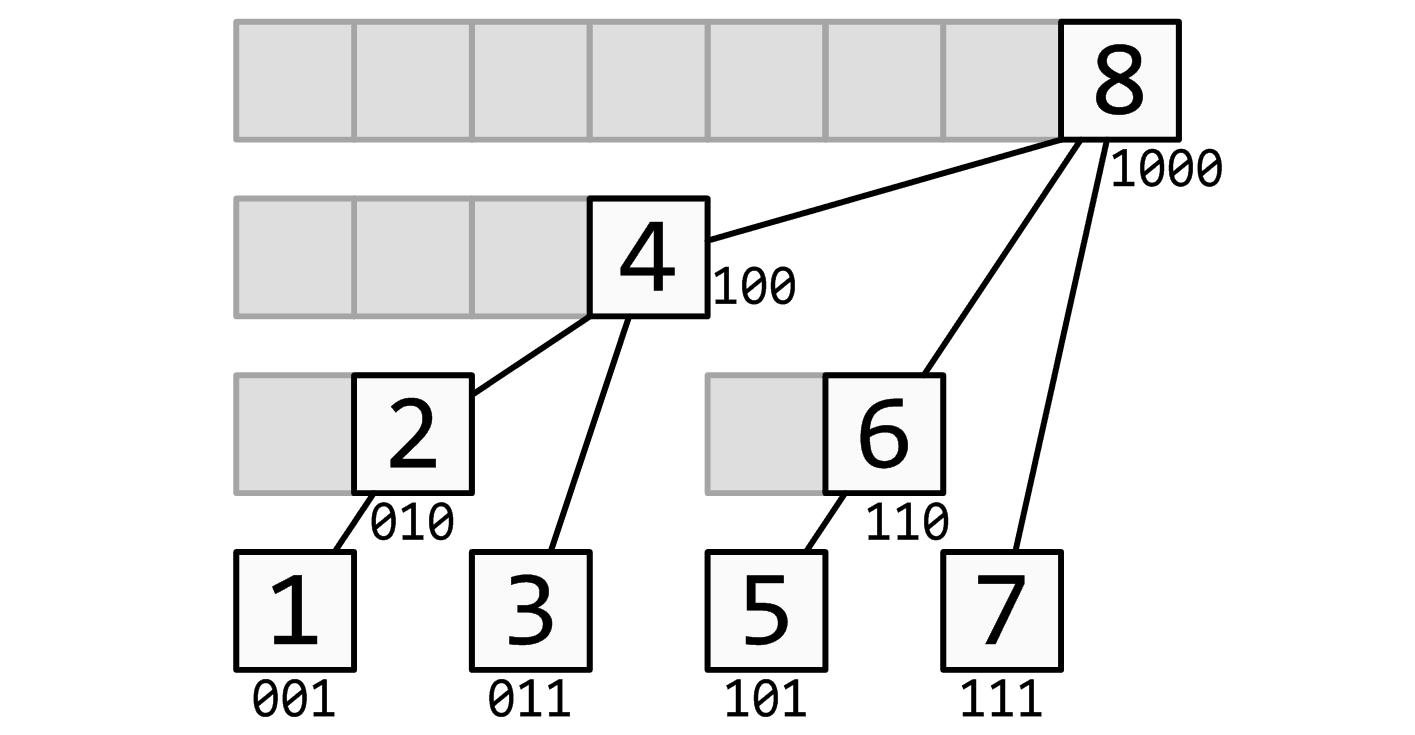
更新的时候，复杂度之所以是 log 级别的，就是需要更新所有的父问题。
如上图，更新 5 的时候，需要更新 6，需要更新 8，一直需要更新到 maxn，最多有 log(n) 个父问题。

如上图，查询 8 的时候，可以直接O(1)得到答案。
而查询 7 的时候，会拆分为三个子问题：7、6、4 直接相加得到答案，最多可以拆分为 log(n)个子问题。

四、树状数组的模版

树状数组可以封装为一个对象，提供初始化、更新、查询三个方法。

这样，你需要使用树状数组的时候，创建一个对象即可。

五、最后

这里给大家分享了树状数组的模版，代码具体位置在如下，感兴趣的可以自己去获得文本的模版。

文本模版地址： https://github.com/tiankonguse/ACM/blob/master/tmpleate-2020/code/treeArray.cc

《完》

-EOF-

本文公众号：天空的代码世界
个人微信号：tiankonguse
公众号ID：tiankonguse-code