必备算法模版之离线化

一、背景

之前我分享 leetcode 算法比赛题解的时候，经常会提到这个题裸用树状数组就过了，那个题裸用线段树就过了。

那怎么裸用呢？
现场根据自己的硬实力敲一个树状数组或者线段树吗？

不是的。
这些固定的算法都有固定的代码，没必要重复敲一遍。
直接从代码库里复制过来就行了。

这里的代码库我们称为模版。

今天给大家分享一个大数据离线化的模版库。

二、离线化解决什么问题

先来看一个问题。

假设这里有一个数组，数值范围是32位整数，求每个位置左边比自己值小的个数。

正常情况下，每个位置需要在前面循环一遍比较求出答案。
复杂度 O(n^2)

此时你可能会想，对前面的数据先进行排序，然后再怎么二分得到答案。
但是，排序需要 n 次，复杂度就是n^2 log(n)了。

我们换一个思路，假设每个数字值都对应另外一个数组的下标，默认值都是 0。
每遇到一个数字，这个数字对应下标的值就加 1，代表这个数字出现一次。
这样问题就转化为了一个前缀和的问题。

如果输入数组的数值范围比较小且都是正整数时，可以通过前文提到的《树状数组》来解决。

但是数值范围比较大，甚至有负数的时候，就不能直接把数字当作下标来计算了。

此时，通过离线化这个方法，就可以解决大数据储存不下来的问题。

三、离线化的原理

离线化的本质就是对较离散的大数据进行重新编号，映射为较小的数据，从而可以使用数值当作下标来进行各种数据结构计算。

具体实现也很简单，即统计都出现哪些数字了，为这些数字从小到大重新标号。

比如输入数据是 3 50 3 100 50。
去重后有三个数字3 50 100，编号为1 2 3。
此时输入就可以转化为 1 2 1 3 2。

上面提到的问题，转化为小数据后，就可以使用前文提到的树状数组来解决问题了。

四、离线化的模板。

大数据离线化可以封装为一个对象，提供初始化，添加大数据、离线化、查询的操作。

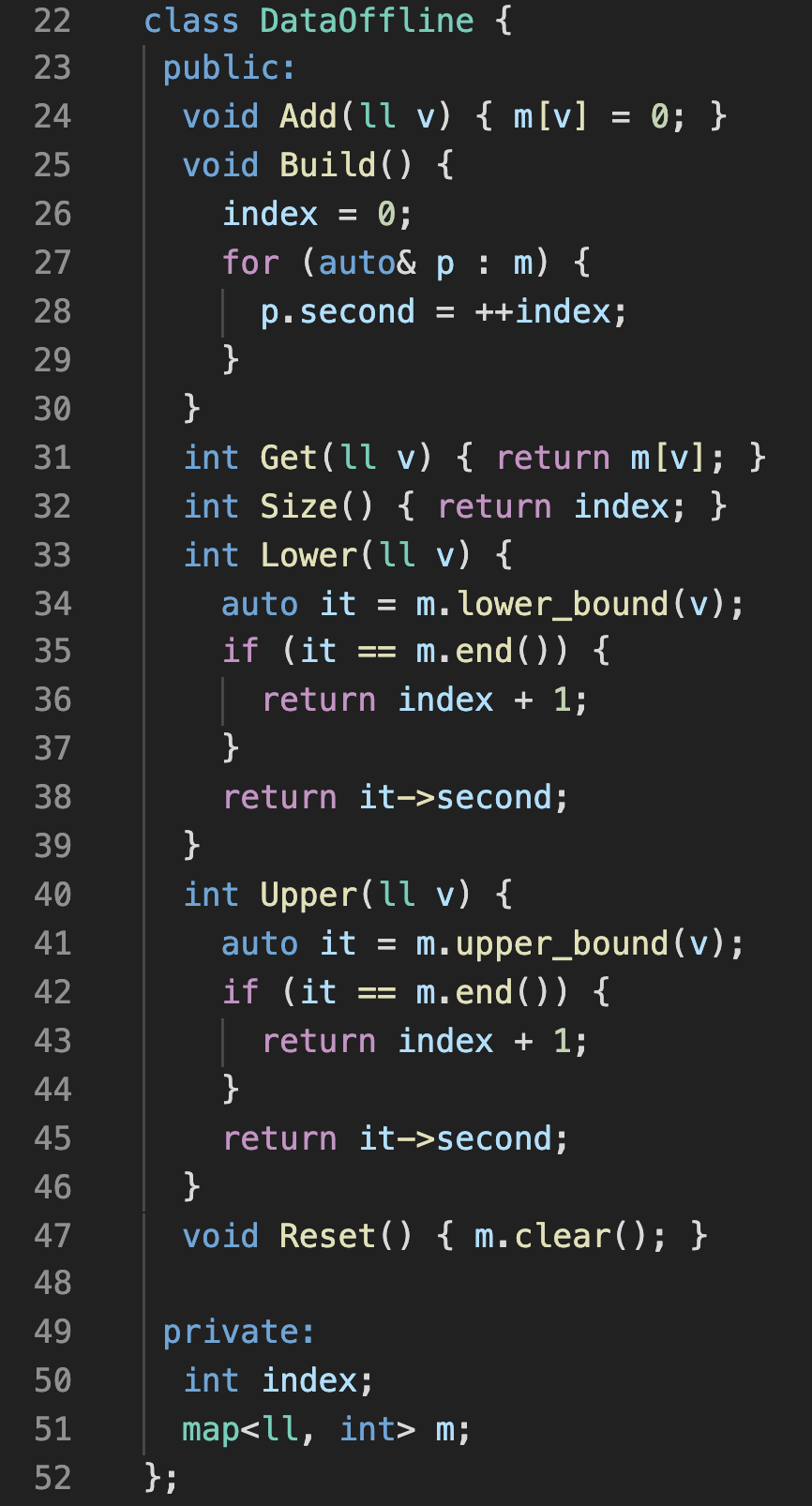
这样需要对大数据离散化的时候，创建一个对象即可。

五、最后

这里给大家分享了大数据离线化的模版，代码具体位置在如下，感兴趣的可以自己去获得文本的模版。

文本模版地址：https://github.com/tiankonguse/ACM/blob/master/tmpleate-2020/code/dataOfferLine.cc

《完》

-EOF-

本文公众号：天空的代码世界
个人微信号：tiankonguse
公众号ID：tiankonguse-code