初级树状数组 leetcode 练习题

一、背景

之前分享了《树状数组模板》和《离散化模板》，今天来看几道练习题。

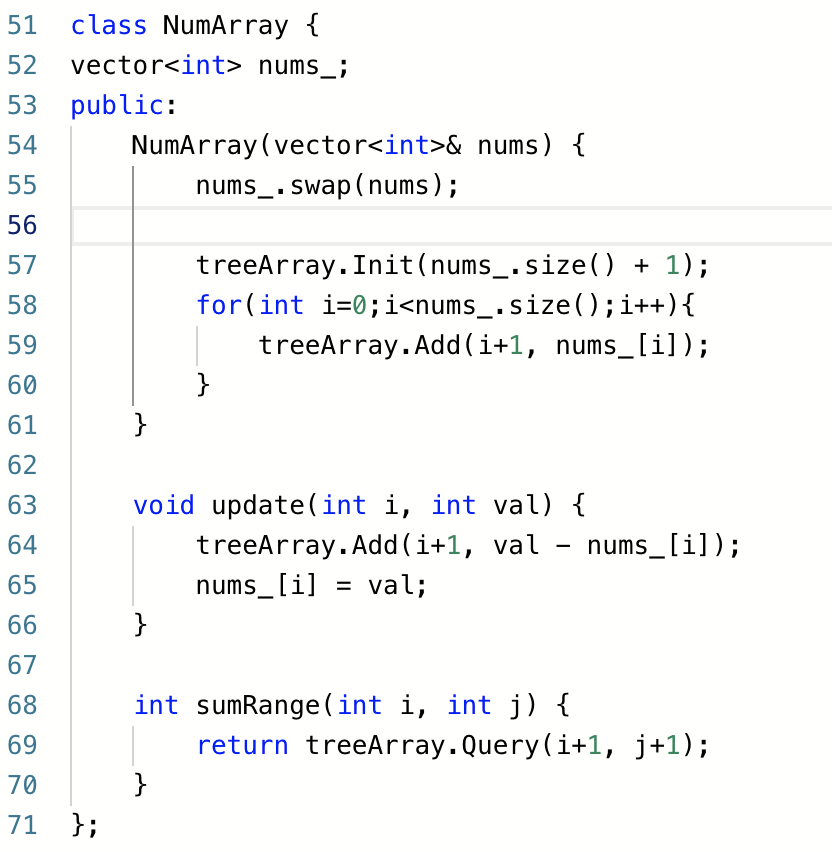
二、区域和检索 - 数组可修改

题意：给一个数组，有两个操作。 1）求区间[l,r]的和。
2）修改下标 i 的值为v。

思路：题意是单点更新，求区间和。
赤裸裸的树状数组模板题，直接套用即可。

代码：https://github.com/tiankonguse/leetcode-solutions/blob/master/problemset-new/003/00307-range-sum-query-mutable/range-sum-query-mutable.cc

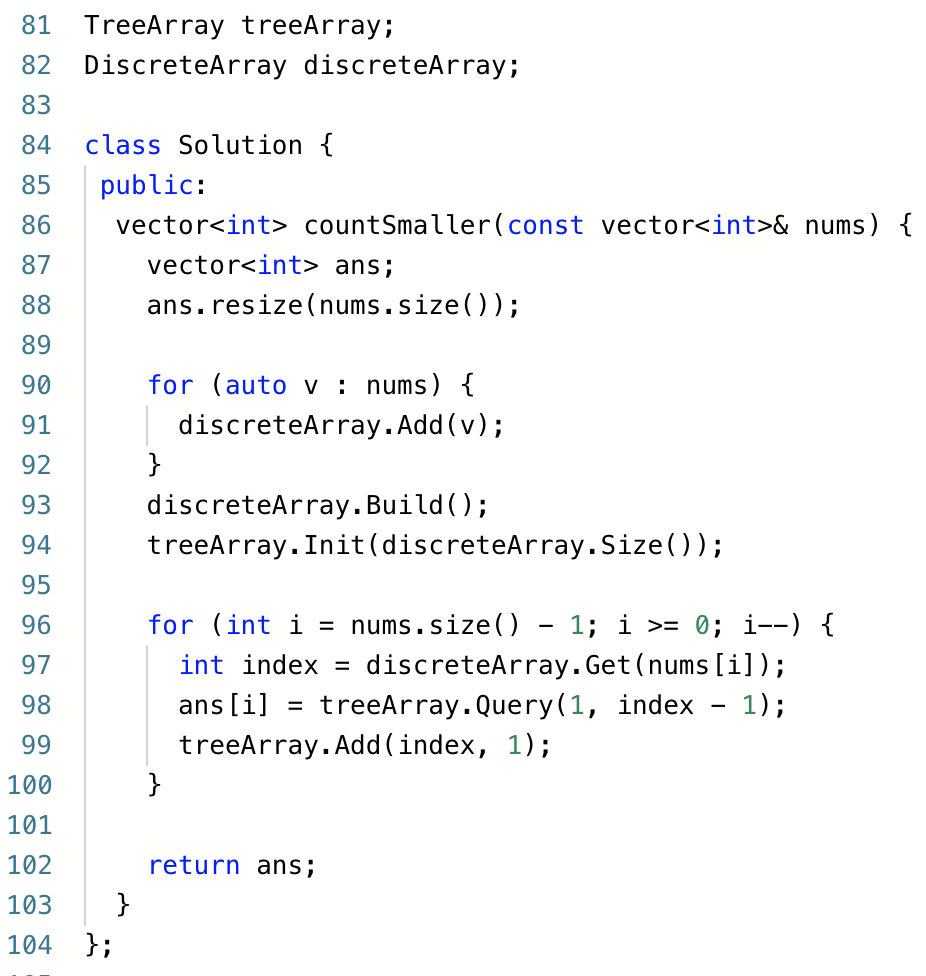
三、计算右侧小于当前元素的个数

题意：给一个数组，求每个位置右侧比自己小的元素个数。

思路：如果不看数据范围的话，裸套树状数组模板即可。
具体细节是从后到前遍历，先通过前缀和求出小于自己的元素个数，然后把自己再加入到树状数组中。

这道题的元素值很大，所以需要使用离散化模板进行重新标号。

代码：https://github.com/tiankonguse/leetcode-solutions/blob/master/problemset-new/003/00315-count-of-smaller-numbers-after-self/count-of-smaller-numbers-after-self.cc

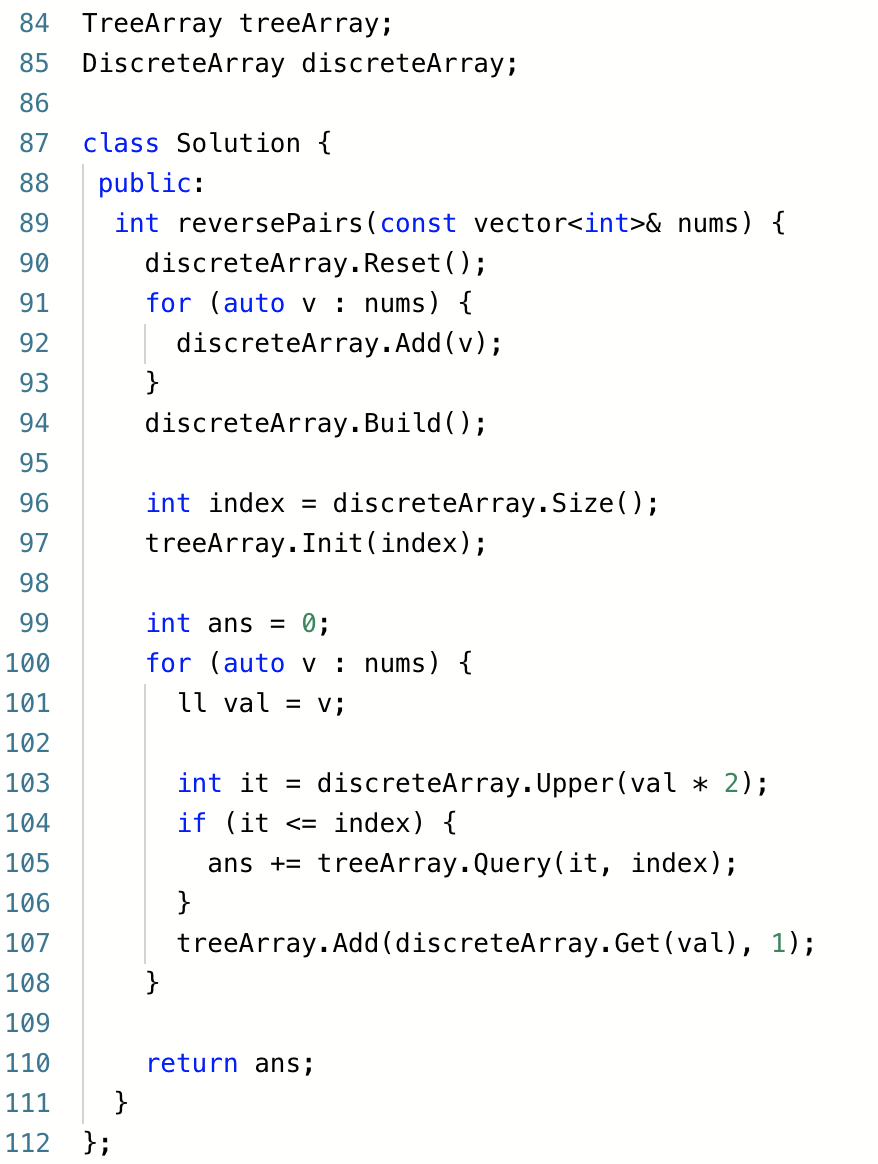
四、翻转对

题意：给一个数组，求每个元素左侧大于两倍当前值的元素个数。
使用数学公式就是，求 i<j 且num[i] > num[j]*2 的个数。

思路：与上一题类似，只是大小关系只是变成了两倍。
求大于当前值的个数，其实就是求后缀和了。

所以只需要使用 Upper 算法找到第一个大于两倍值的下标，然后求后缀和即可。

代码：https://github.com/tiankonguse/leetcode-solutions/blob/master/problemset-new/004/00493-reverse-pairs/reverse-pairs.cc

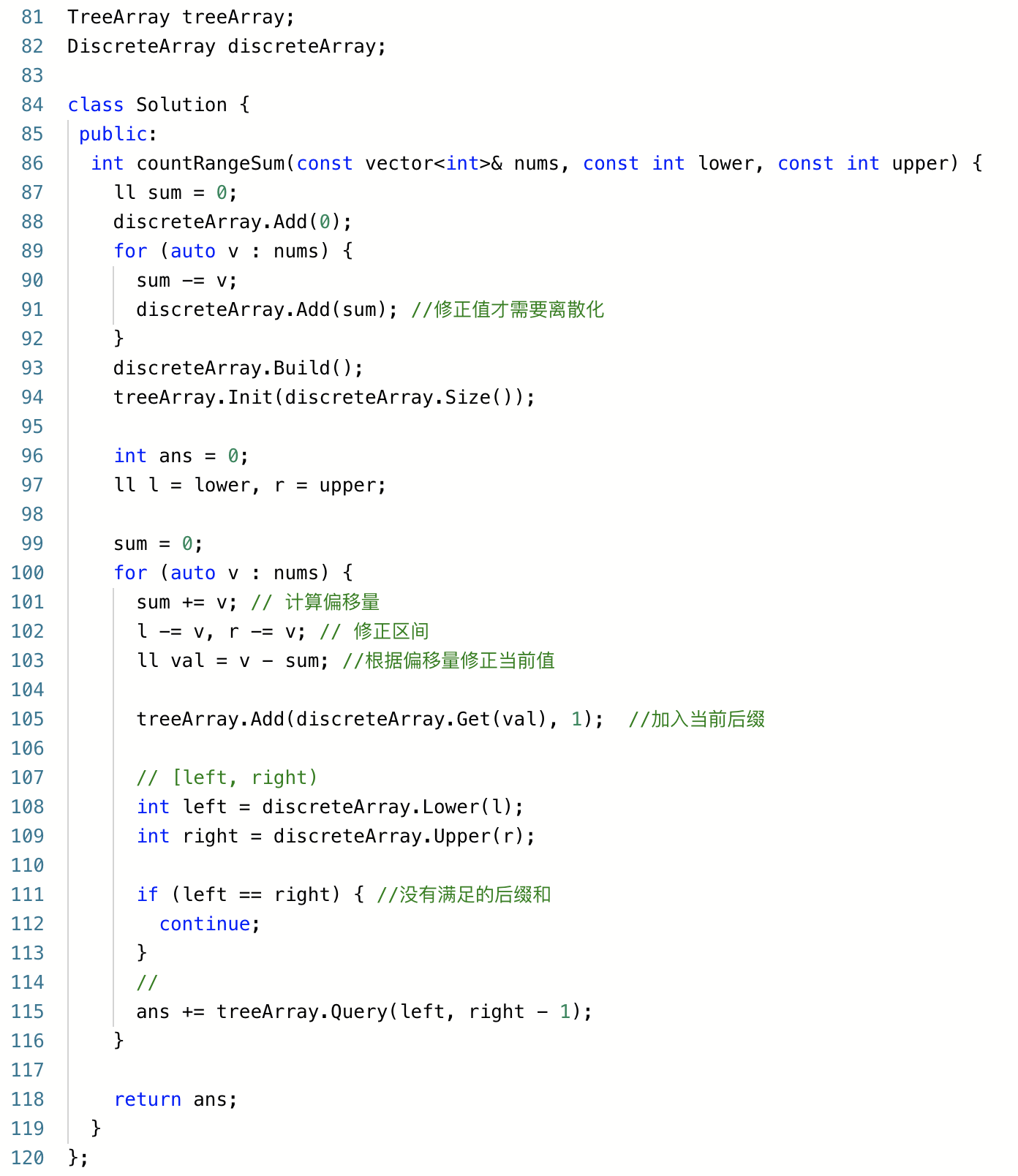
五、区间和的个数

题意：给一个数组，问区间和在[lower, upper]范围内的区间个数。

思路：暴力是O(n^2)的复杂度，我们需要想出一个更快的算法来。

我们可以思考这样一个情况。
从左到右扫描数组的时候，假设当前位置是j。
如果我们能快速找到以j为后缀的满足要求的区间，那就可以快速找到答案了。

再进一步假设。
假设我们已经有所有以j为后缀的区间和了，储存在树状数组里。

sum[1  , j]
...
sum[j-2, j]
sum[j-1, j]
sum[j  , j]

那就可以log(n)的复杂度来查询后缀和在区间[l, r]的个数了。

那如何由第j个元素的后缀和转化为第j+1个元素的后缀和呢？

j的所有后缀和加上nums[j+1]，就几乎都是j+1的所有后缀和了。

sum[1  , j] + nums[j+1]
...
sum[j-2, j] + nums[j+1]
sum[j-1, j] + nums[j+1]
sum[j  , j] + nums[j+1]
              nums[j+1]

上面的话聚合在一起就是求 j的所有后缀和 加上 num[j+1] 后，值在范围 [l, r]内的个数。

那反过来，根据小学二年级学的一个性质，两边同时减去一个数字，答案不变。
所以 区间[l, r] 和 j的所有后缀和可以都减去nums[j+1]。
问题就转化为了所有 j的后缀和满足区间 [l-nums[j+1], r-nums[j+1]]的个数。

到这里，不知道你是否还明白在说什么。
简单的说，我们通过修改区间[l, r]就可以将j+1的后缀和问题转化为j的后缀和问题。

这里唯一需要注意的就是，最后一个元素nums[j+1]不是j的后缀和，所以没办法直接减去nums[j+1]。
所以这里需要通过原始的[l,r]与 j的区间进行偏移修正，将nums[j+1]转化为j的后缀和形式。

修正的值其实也很容易计算。
通过j到j+1的关系，可以发现修正一次的偏移量是nums[j+1]。
那么j到j+2修正偏移量就死活nums[j+1]+nums[j+2]了。

提取规律，第k个值需要修正的偏移量就是前缀和sum[1, k]了。

代码：https://github.com/tiankonguse/leetcode-solutions/blob/master/problemset-new/003/00327-count-of-range-sum/count-of-range-sum.cc

六、最后

这四道树状数组的题都很有特征。

第一道是裸套模板。
第二道是稍微变通一下来套模版。
第三道则存在非离散化的数据，需要使用Upper或者Lower来查找第一个满足情况的下标。
第四道题则属于最难的，需要反向修改查询的区间，这种思路可以学习一下，是个不错的思路。

《完》

-EOF-

本文公众号：天空的代码世界
个人微信号：tiankonguse
公众号ID：tiankonguse-code