【算法】Leetcode 第126场比赛回顾

一、背景

前面做过 Leetcode 的第 88 场比赛，并写了《Leecode 第88场比赛回顾》笔记。
今天简单的做了 Leetcode 第 126 场比赛，也简单的记录一下。

二、查找常用字符

题意很简单，给一些字符串，求字符串的公共子序列。
这里还要求，允许字符串乱序，输出的时候公共子序列从小到大输出。

如果纯粹是公共子序列，那么这道题就需要使用一些高级数据结构才能解决。
但是这里允许字符串乱序，那这个问题就可以简化为计数问题了。
求多个字符串的公共子序列，其实就是循环依次求每个字符串和当前答案的公共子序列，即循环合并即可。

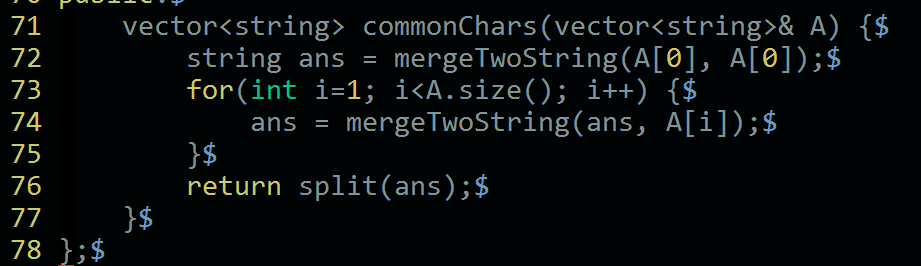
而对于两个字符串的计数合并，则是对每个字母计数统计，然后分别取最小值即可。

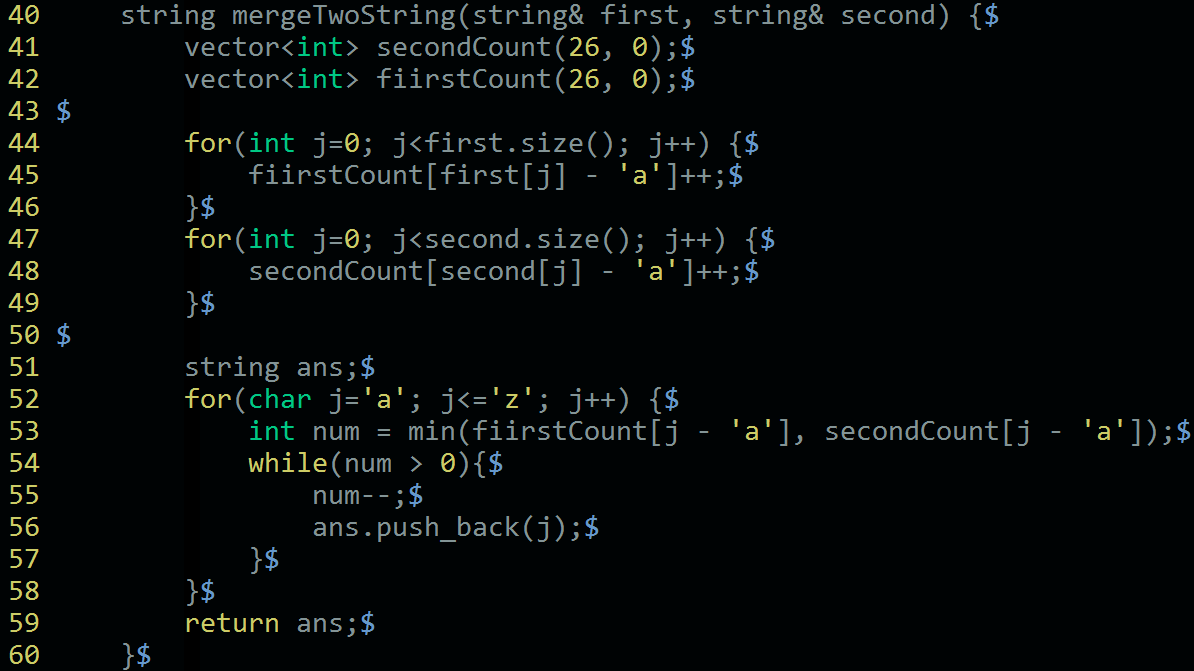
至于字符串拆分，就是一个循环而已，这里就不上代码了。

当然，我实际做的时候，没有拆分为三个函数，而是一个循环搞定的，这里拆分为三个函数好方便大家理解。

三、检查替换后的词是否有效

具体题意是：abc 字符串为有效字符串，我们把abc插入到一个有效字符串里面形成的字符串也是有效的。

例如abc插入到abc有四种插入法：
插入到最前面，形成abcabc有效字符串。
插入到第一个位置a之后，形成aabcbc有效字符串。
插入到第二个位置b之后，形成ababcc有效字符串。
插入到最后面，形成abcabc有效字符串。

问题：判断给定的一个字符串是否是有效的。

这道题是一个常见的题型：检查数据是否符合某种递归的模式。
最经典的就是括号匹配问题。
而对应的解决方案就是使用栈来解决。

对于递归模式，之所以能够使用栈来解决，就是因为扫描前面的数据时，暂时不知道是否满足对应的递归模式。
而我们使用栈暂时把前面的数据保存起来，当检查发现满足模式后，逆向的执行这个模式，就可以逆向的递归缩短字符串。
如果给定的字符串满足要求，则扫描完出入字符串后，栈里面也应该刚好为空。

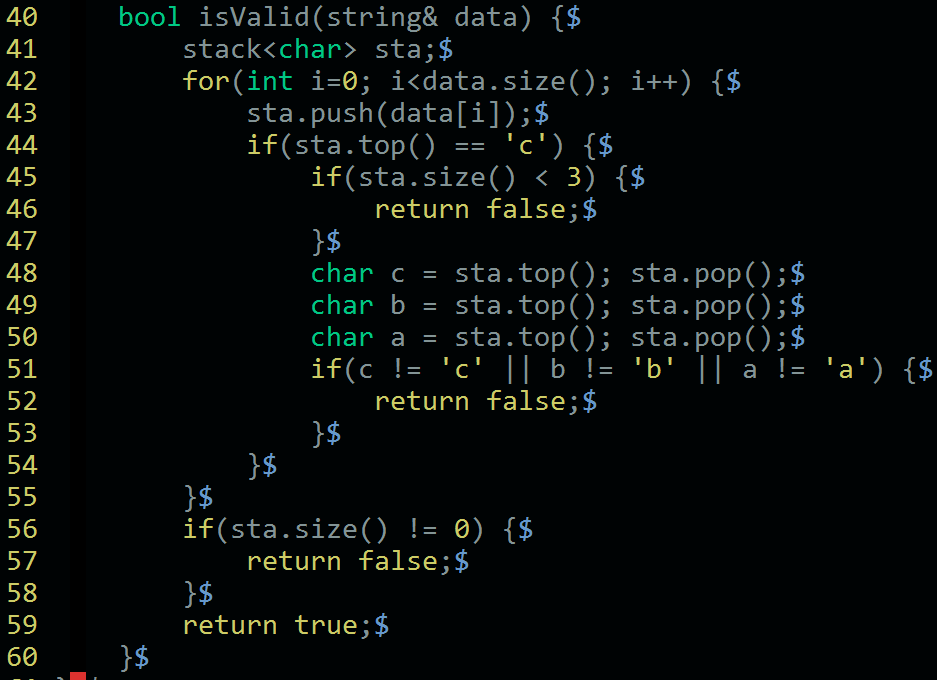
具体到这道题，则是发现第一个字符c时，栈顶的两个元素肯定依次是b 和 a。 如果不满足，则不是有效字符串，如果满足，则继续下去即可。

四、最大连续1的个数 III

题意：给一个有0和1组成的数组，我们最多允许对K个0的值变为1，求仅含1的最长连续子数组的长度。

如果你看我上篇文章《Leecode 第88场比赛回顾》的话，会发现也有一道类似的题。
那道题是给了一堆0和1，求挑一个0使得这个0距离最近的1最远。
我们的方法是累计计算中间的连续0的个数，然后算出答案来。

那对于我们这道题，其实可以使用类似的思想，不过这里允许0不连续，并且最多只能累计K个0。

具体来说，就是维护一个队列，这个队列需要满足两个条件。
一、队列里面的数字是连续的。
二、队列里面0的个数不超过K个。
而我们的答案就是队列的最大长度。

而代码实现，则是扫描输入的数据，一次入队，并更新队列0的个数。
如果0的个数超过限制，则队首需要不断出队，直到满足不超过K个。
具体如下：

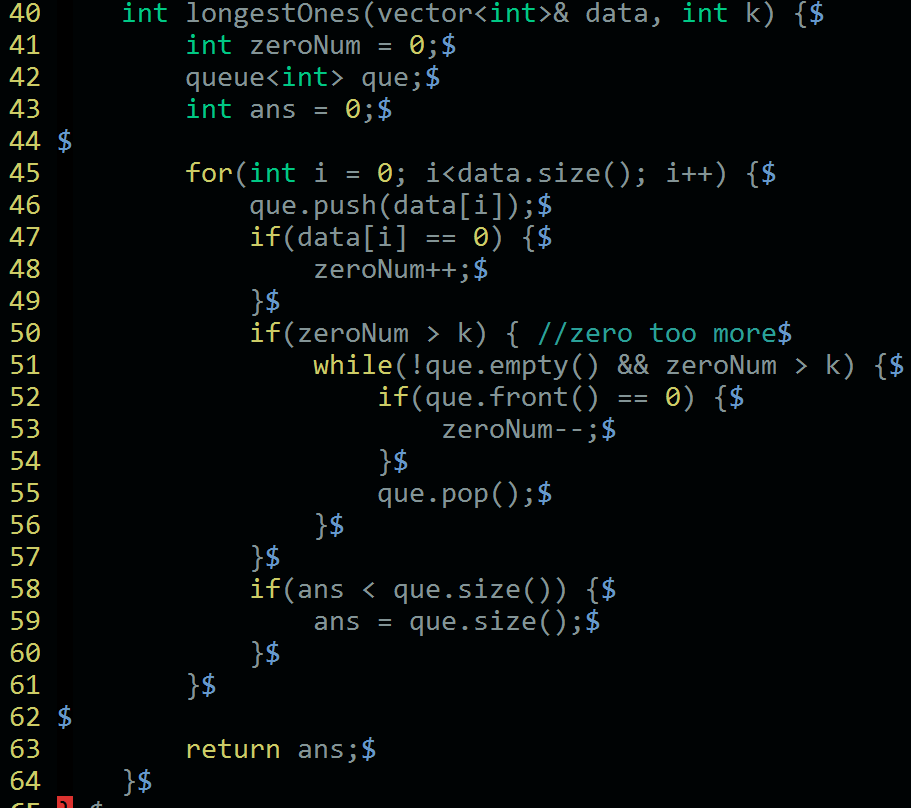
这里面有个主意实现就是，当不满足条件时，需要循环出队。因为队首可能不是0。
由于我们确定不满足条件时，0的个数肯定是K+1个。我们也可以直接先把队首的1出队，然后再出一个0。

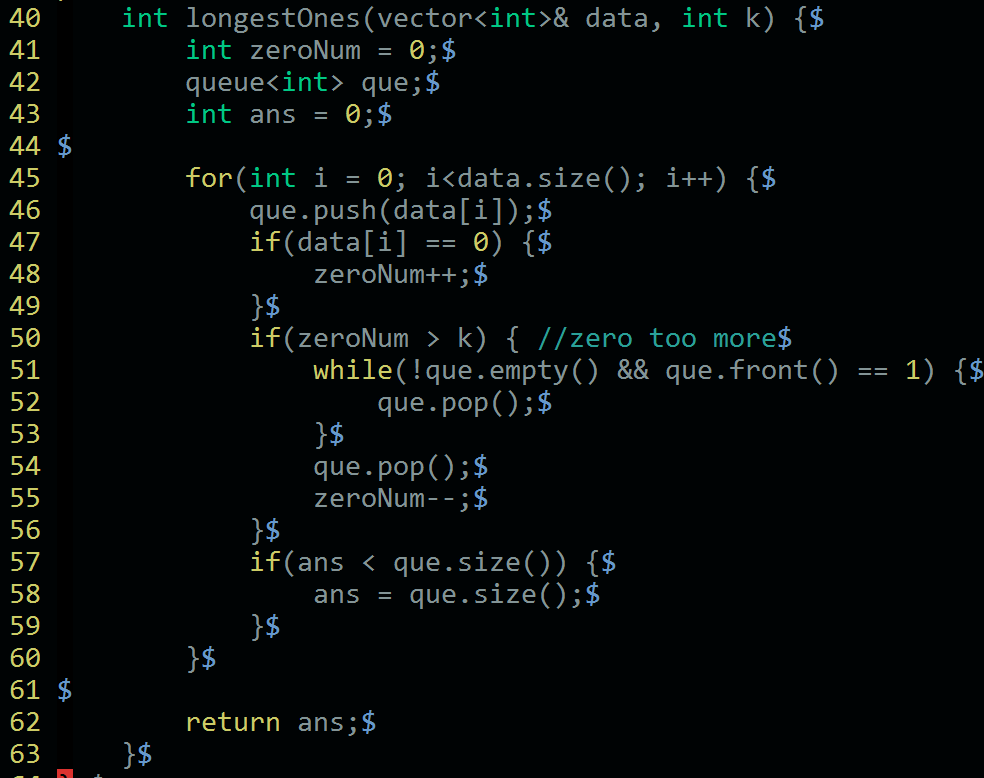
当然，两个思想在逻辑上是等价的，不过第一个算法更通用写，而后面这个则更个性化。

五、合并石头的最低成本

题意是给K堆石头，每堆知道有多少个。
然后会对这些石头进行合并，每次把连续的K堆石头合并为一堆，成本是这K堆石头的总个数。
要求不断的合并下去，直到所有石头合并为一堆，求最小成本。
如果不能合并为一堆，则返回 -1。

面对这道题，我们首先需要判断是否能合并为一堆。
简单观察即可发现，每合并一次，石头的堆数就减少K-1。
所以我们可以推导出这样一个等式：N - p * (K - 1) = 1，其中N是石头的总堆数，p是合并的次数。
公式转化一下，则可以得到一个判断是否有答案的不等式：(N - 1) % (K - 1) == 0。

接下来，就是假设有答案，怎么得到最优的答案了。

其实，在看到这个问题时，第一眼想到的是哈夫曼树。
但是哈夫曼树的策略是贪心算法，即不断的挑选最小的K个数字，而且很容易证明其正确性。
而我们这道题必须是连续的K个数字，贪心的话还无法证明其正确性，所以需要换个思路了。

既然是类似于哈夫曼树的题，就应该先来看看这颗树长什么样子，树的图形画出来后，题就变得比较形象了，一般也可以找到一种可视化的方案来。

比如对于第一个示例，输入是stones = [7,7,8,6,5,6,6], K = 3，我们可以手动画出下面的最优树。

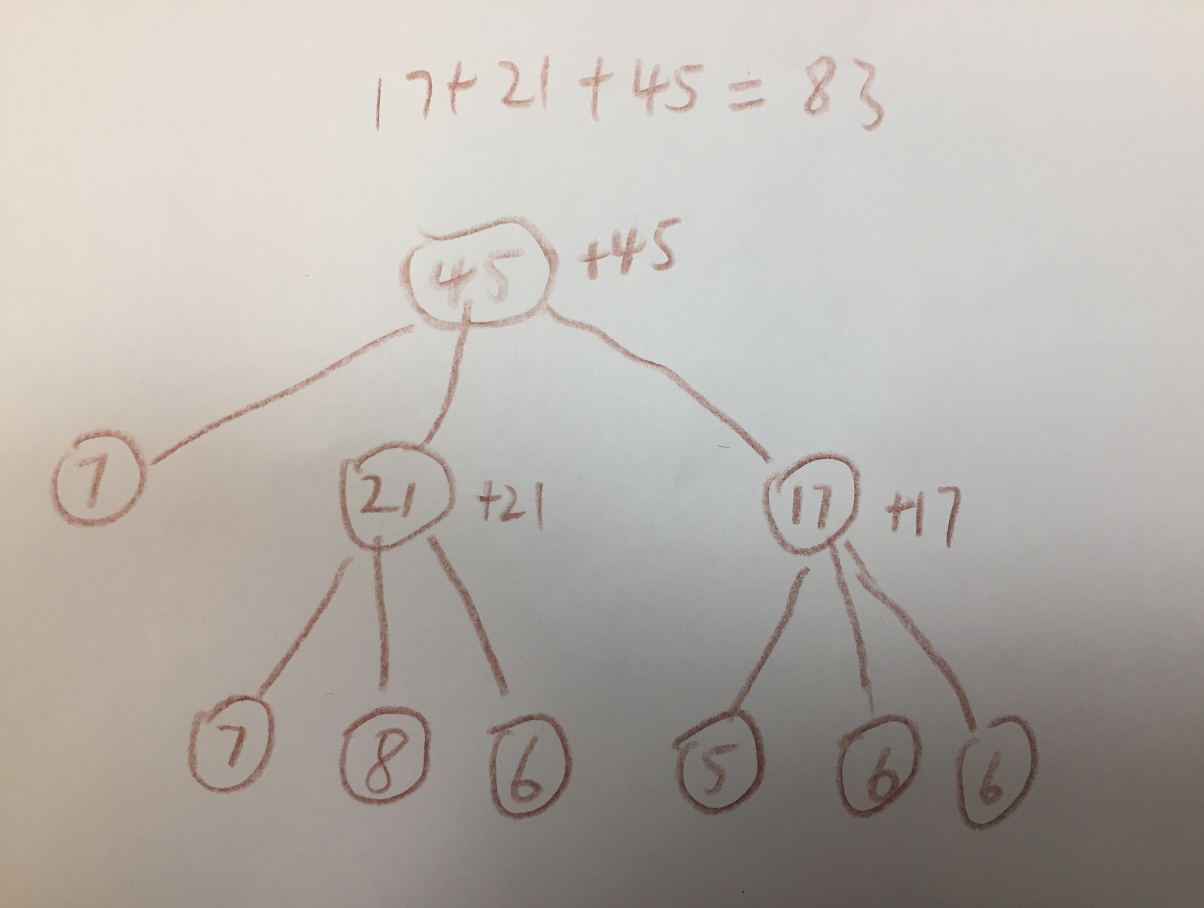
我们观察这个树之后，可以发现这个问题可以划分为一系列子问题来解决，大概如下图。

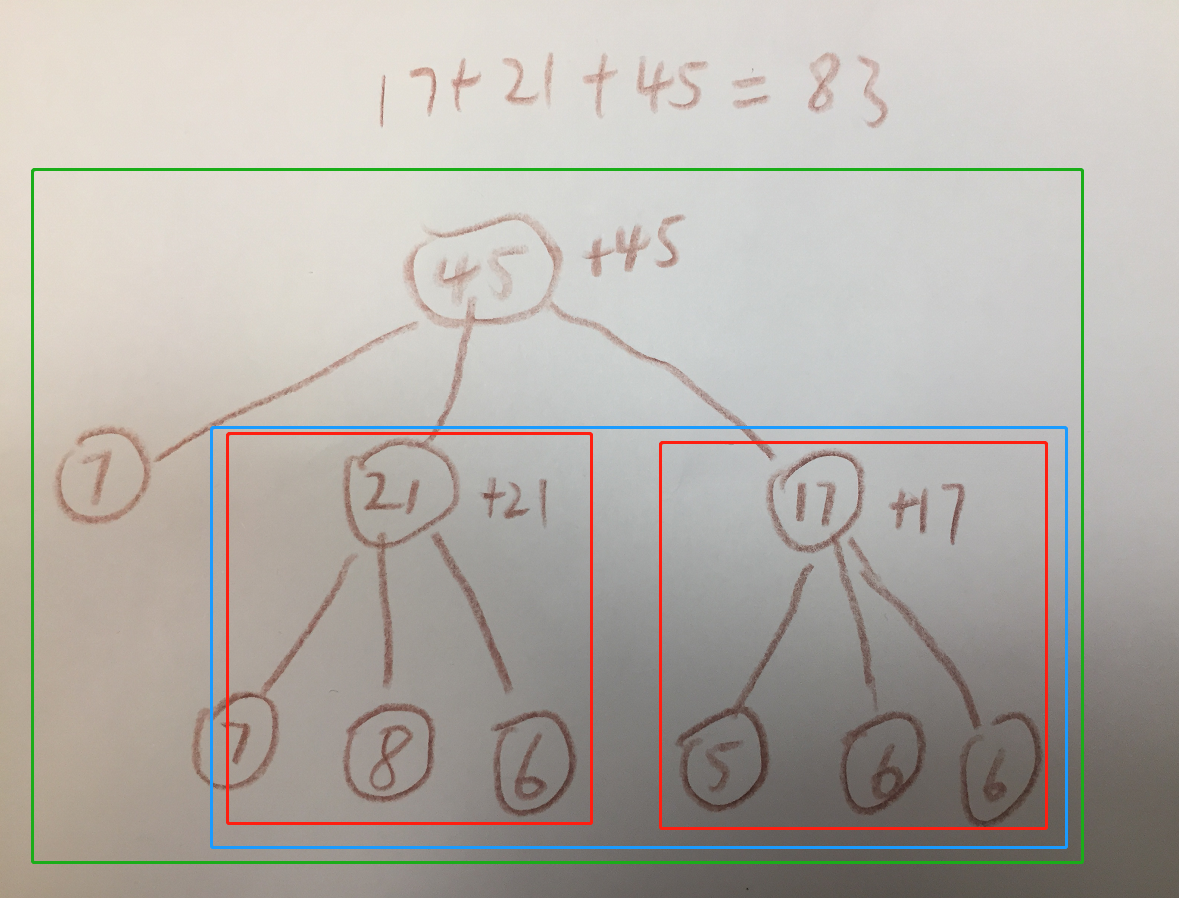
我们对于给如的数组序列，随意的划分为两部分，使得第一部分合并为1堆，第二部分合并为K - 1堆。
这样的划分有很多，最优答案肯定是其中一个划分（根据最优答案反推，我们可以划分出这样的图）。

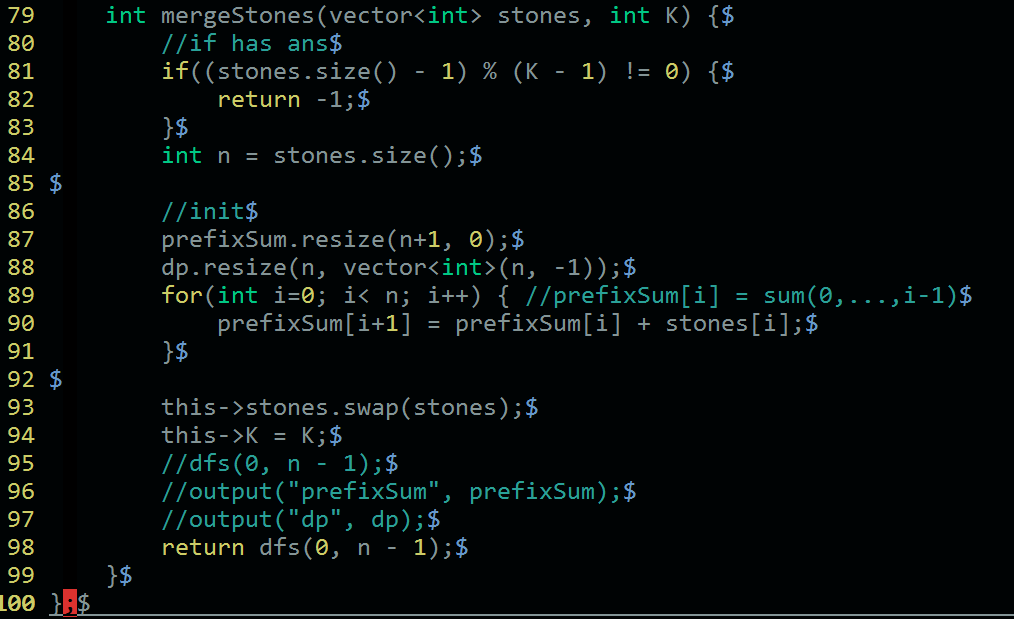
既然这样，我们就可以写出对应的递归代码了。

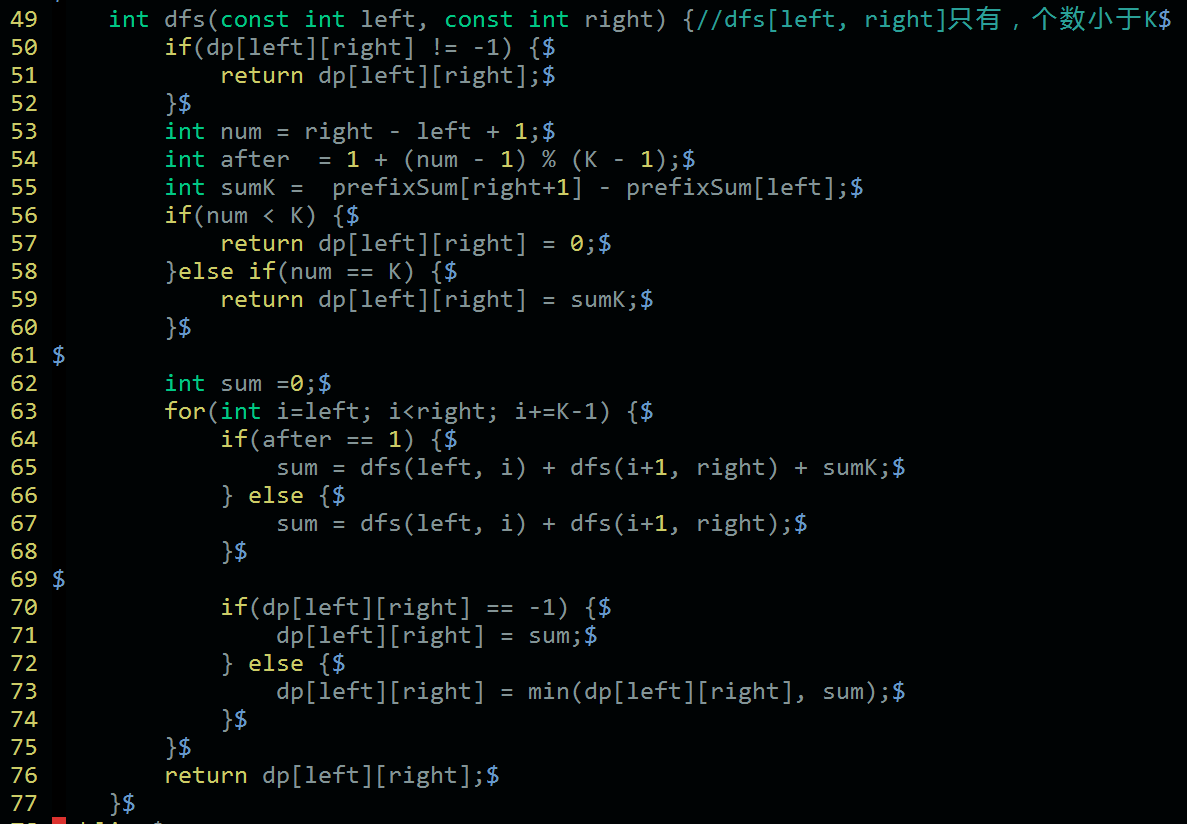
代码里面有一个出口。
第一个是是否已经计算过，计算过则直接返回。
第二个是这个区间是否不足K个，不足则不需要合并，即答案是0。
第三个是这个区间是否刚好K个，这个时候直接合并为1个，答案就是区间和。
第四个就是上面我们提到的划分，在多个划分中找到最小的答案。

在计算划分的时候，有个注意事项就是，只有两个划分可以合并时，我们才需要加上区间和。

而对于输入，我们只需要初始化一下dp数组，然后计算前缀和即可。

六、最后

这次的四道题其实还是比较有点技术含量的，涉及到统计计数、堆、栈、动态规划四个知识点。

另外，上篇文章提到，上次的时候编程环境弄了好久，现在终于差不多稳定了。
测试的时候，差不多是这个样子。

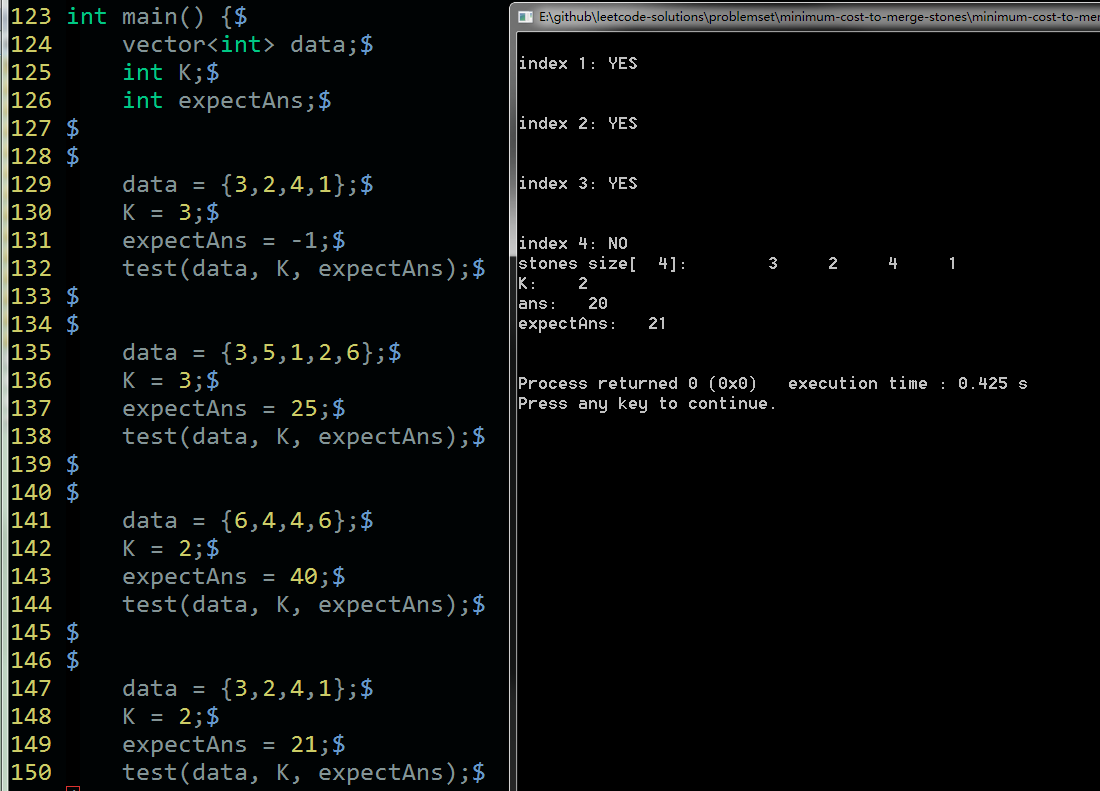
答案对了，直接输出YES，答案错了，输出NO，并把输入和输出都输出来。
想要我的模板的，可以公众号后台回复leetcode获取源代码。

-EOF-