【算法】双指针就是这么简单

一、背景

这篇文章不仅仅介绍了双指针的使用方法，还教你怎么分析一道算法题，并由简单粗暴的方法，慢慢演变到最优的方法。
注：每次我都会把对应的练习题地址发送到群里，建议想学算法的朋友耐心的做一下这些题。

二、双指针简介

双指针的含义是数组中的两个指针，也可以是数组的两个下标。

双指针一般有两种用法。
第一种是一个指针从头向后移动，另一个指针从尾部向前移动。
第二种是两个指针抖从头部向后移动，但是一个移动的快，一个移动的慢。

下面分别来看看对应的实际使用场景吧。

三、反转字符串

如果你认真看我上篇文章《字符串就是这么简单》的话，可以发现在第一个例子“二进制求和”中，我们多次用到字符串反转。
在代码里我直接使用了 STL 自带的反转函数 std::reverse。
现在我们需要自己来实现这样一个函数。

面对这道问题，最简单粗暴的方案就是新开一个数组，循环一遍即可，复杂度O(n)。
我们使用双指针技术，则可以找到一个更优的方案，复杂度虽说也是O(n)，但是计算相同的数据，速度提高了一倍。

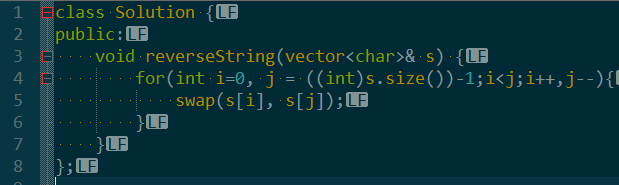
具体来说，循环数组时，使用两个下标，一个指向首部，一个指向尾部。
每次先判断是否已经完成反转，未完成则交换两个下标的值，然后头部下标向后移，尾部下标向前移。
等完成反转后，我们可以发现头部下标循环了数组的前半部，尾部下标未还了数组的后半部。

四、数组拆分 I

告诉你2n个数字，将这些数字划分为n对，例如 (a1, b1), (a2, b2), ..., (an, bn)。
求一种划分，使得1到n的min(ai, bi)的和最大。

这道题的题意使用人话说，就是将数字两两划分后，在每对数字里面选最小的数并求和，求和最大的划分。

由于每对都取最小的数字，可以确定，所有数字里面最小的数字肯定会被选出来。
接着这个最小的数字可以免费带走一个数字，那我们肯定选择带走第二小的数字啦。
按照这个逻辑来，这道题的思路也就出来了。

先把所有数字从小到大排序，假设下标从0开始，我们只挑选偶数下标的数字即可。

五、两数之和 II

题意：输入一个按照升序排序的数组，求找两个不同的数字，使得他们的和等于目标数字。

这道题虽然很简单，但是很有意思。
因为可以实现的方法特别多，可以当做面试题来考察对方。

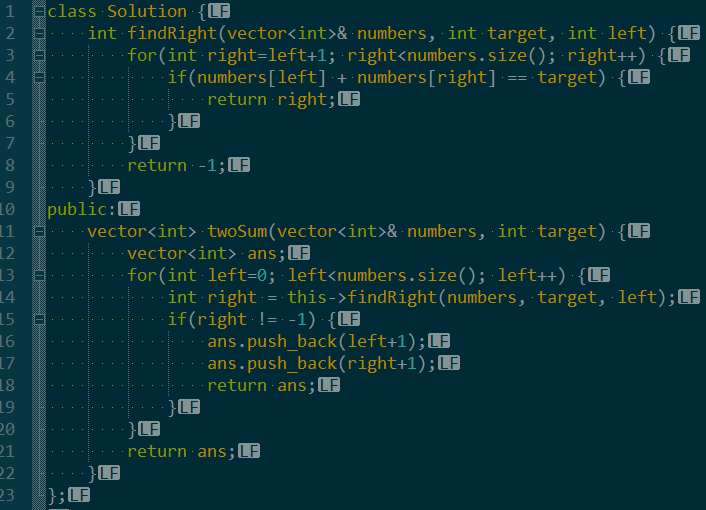
面对这道题，第一个可以想到的方案就是枚举暴力查找。
即循环假设选择第一个数，然后在后面循环查找是否存在答案。
由于有两层循环，复杂度是O(n^2)。

当我们问是否可以优化时，可以发现后面循环查找可以优化。
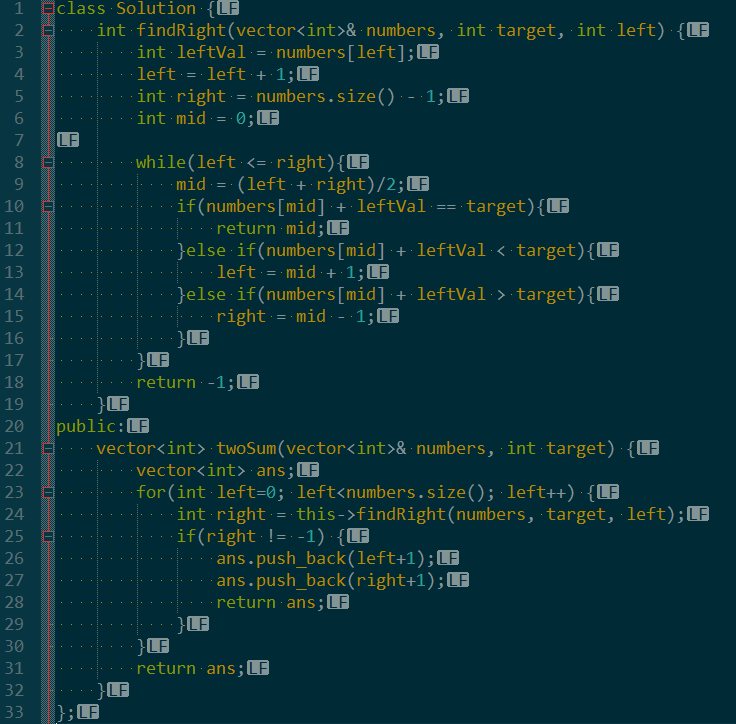
我们的目标是判断第一个数字和第二个数字之和是否是目标数字。第一个数字和目标数字已经确定了，可以反向计算出第二个数字的值。
待查找的数组是有序的，自然可以使用二分查找了。
这里最外层一层循环，里面二分查找，复杂度是O(n*log(n))。

PS：我之前曾介绍过《二分查找》，感兴趣的可以去看看。

我们使用了二分查找提高了查找速度，那我们能不能更快的解决这个问题呢。
这就需要研究一下这道题的特征了。

特征一、数组有序。
特征二、求两数字的和等于目标数字。

假设我们选择的第一个数字是从小到大的，例如选择了下标为0的数字。
如果与最后一个数字之和大于目标，是不是意味着第一个数字不管选哪个，最后一个数字都不会是答案呢？
既然最后一个数字不可能是答案，是不是我们可以将数组的范围减小一些呢？

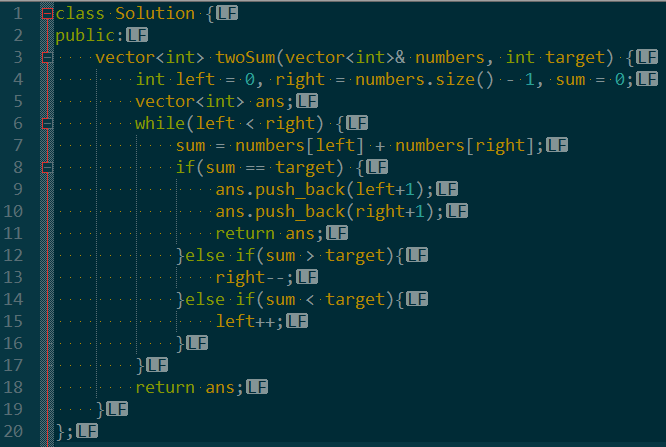
每次选择第一个数字后，我们依次更新数组的边界，直到之和小于等于目标。
等于则找到答案了，结束。小于则代表选择的这个数字没有答案，迭代到下个数字去。
按照这个思路来看这道题，突然发现找到了一个新大陆：这道题竟然可以在O(n)复杂度内完成计算。

六、移除元素

题意：给你一个数组，将所有数组值等于val的元素删除，并返回新数组的长度。
要求：删除过程中，不能申请新的数组，原数组的长度也不能变。

这道题显然是一个面试题了。
如果允许改变原数组的长度，那找到一个直接删除一个就行了，时间复杂度是O(n^2)。
如果允许申请新数组，那循环一遍即可得到新的数组，但需要额外的空间复杂度是O(n)。
现在不能申请新数组，那只能在原数组上进行操作了。

假设我们找到了一个元素后，目标用其他位置的元素覆盖当前元素。
一种思路是马上覆盖，另一种是延迟覆盖。

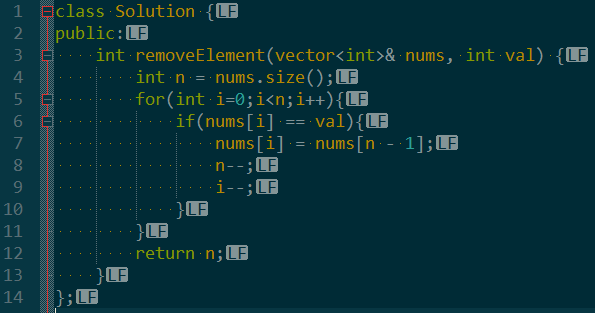
对于马上覆盖的方法，说出来就很容易理解。
当前元素直接和最后一个元素交换，数组的大小减一，重新从当前位置进行判断计算。
什么？不能改变数组的大小？使用另外一个指针或者下标储存这个大小即可。
此时双指针一个是头下标，一个是尾下标。

PS：这个思想面试中经常会遇到，比如数组里随机选几个数字。

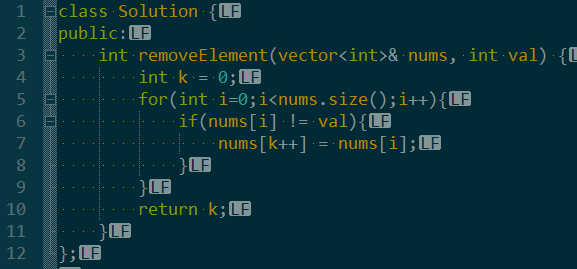
另一个思路是延迟覆盖。
具体含义即使当前这个位置先空着，后面找到需要覆盖的值了，再来覆盖。
这个时候，用一个下标来标记空的位置，用另外一个下标来标记查找的位置。

七、最大连续1的个数

题意：给一个0/1数组，求最大连续1的个数。

这已经是第三次遇到0/1相关的题目了。
这道题也是有多种方法来解决。
一种就计数法，一种就是当前的主题两指针法。

计数法遇到零则重置计数，遇到一则加1，并更新答案即可。

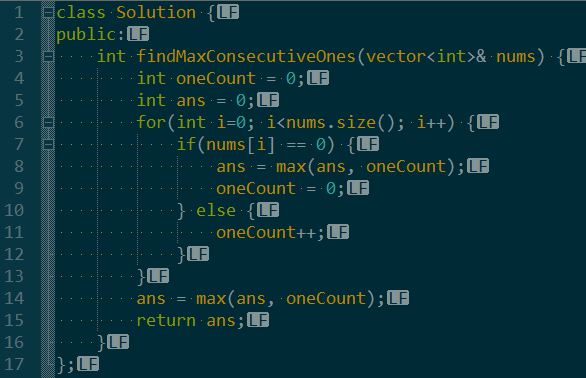
两指针方法和计数类似，遇到零重置指针，遇到一则偏移指针。

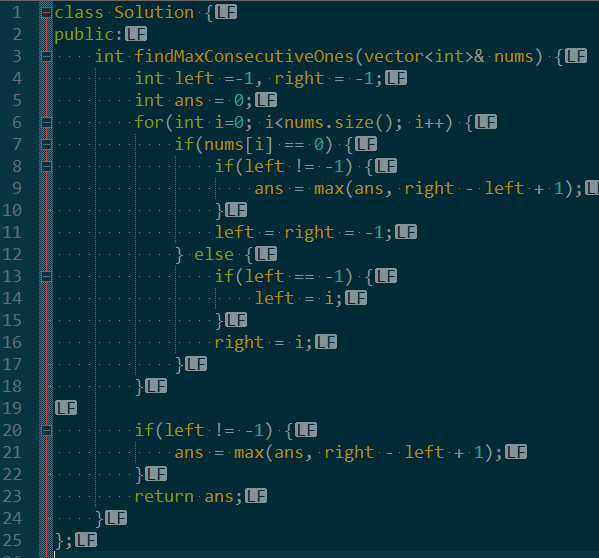
在这两个方法里，都可以看到在最后有一个特殊判断。这是由于数组可能以1结束，此时最后一个答案就没有进行计算。
其实，这个稍微调整一下，就不需要考虑特殊情况了。

八、长度最小的子数组

题意：给一个正数组成的数组和一个正整数S，求一个长度最小的连续子数组，使得它们的和大于等于S。

对于这道题，也是一道面试题。
最简单粗暴的方法就是求出所有的连续子数组，找到最优答案，复杂度O(n^2)。
这个就不上代码了。

面对那么暴露的方案，其实位置确定后，目标是快速找到满足条件的结束位置。
那能不能使用二分呢？
这里需要检查子数组的和，每次子数组的起始位置不一样。
但是我们发现，对于确定的一次查找，那些子数组之和都是前缀数组之和减去固定起始位置的前缀数组之和presum。
于是问题就可以转化为：求前缀数组之和大于S+presum的最小位置。
而对于前缀数组之和，是可以预处理求出所有的前缀数组之和，然后二分的。

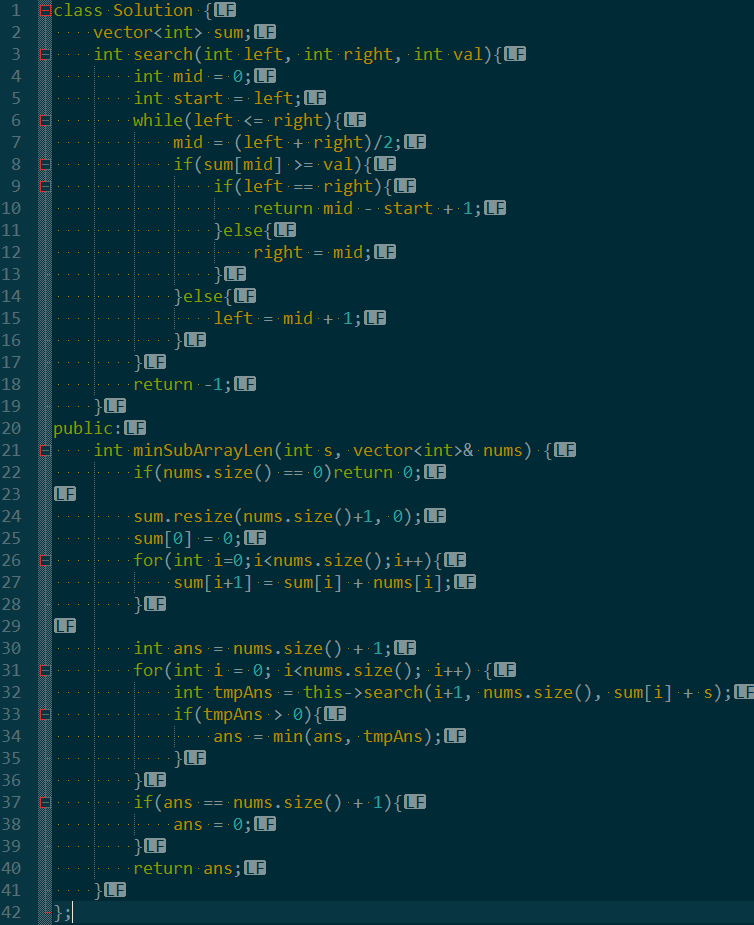
此时，再分析一下这道题，会发现有意思的特征。
假设已经判断a[i] + a[i+1] ... + a[k]首次大于等于S了。
接下来需要查找的是以a[i+1]为起点的数组。
仔细看看a[i]计算的和，可以发现a[i]+...+a[k]已经计算过了，且a[i]+...+a[k-1]一定小于S。
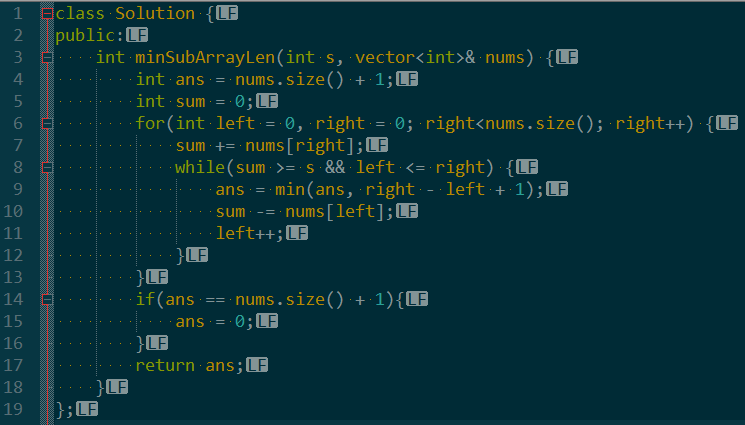
那我们是不是只需要直接从a[i+1] +... a[k]开始计算是否是答案就行了？
这样下来，我们就只需要扫描一遍即可找到最优答案了。

至于a[k]的位置，我们使用另外一个指针或者下标来标记维护即可。

九、最后

回头看看，这个文章里面涉及到的题，都可以拿来当做面试题。
暴力方法是O(n^2)，优化后可以到O(n*log(n))，再优化就可以到O(n)了。

这样的题还有很多，不要想着把这题背下来，而是要学会掌握解决这类问题的思想或者方法。
否则前面出一道很难的背过的题快速答上来了，后面出一道简单的题怎么也答不上来，那很容易判断前面的题是从面试宝典上背的了。

注：每次我都会把对应的练习题地址发送到群里，建议想学算法的朋友耐心的做一下这些题。
-EOF-