【算法】Leetcode 第101场比赛回顾

一、背景

之前已经写了几场比赛记录了，如第126场、第88场、第127场比赛。
上周团队一起做了第101场比赛，现在记录一下题解吧。

二、RLE 迭代器

题号：900
题目：RLE Iterator
题意：给一个数组，按照规则转化为一个计数数组。然后不断的进行出队操作，并返回最后一个出队的值。 数字转化规则（0下标开始）：偶数位置是数量，奇数位置是对应的值。
出队规则：按输入的数量进行出队。

例如，对于输入队列3,8,0,9,2,5，代表依次有3个8，0个9，2个5。
第一次出队2个，则队列变成了1,8,0,9,2,5，最后出队的是8。
第二次出队1个，则队列变成了0,9,2,5，最后出队的是8。
第三次出队1个，则队列变成了1,5，最后出队的是5。
第四次出队2个，则队列变成空了，由于队列不够2个，返回-1代表不够了。

这道题的范围很有意思。
数组大小不超过1000个，数组的值则是10^9个，出队次数也不超过1000个。

如果你想着先把数组按计数展开，则是不现实的事情。
而我们直接按题意从前到后去模拟，算法反而是最优的，累计复杂度是O(n)。

PS：这里的累计复杂度指的是，所有出队操作累计起来的复杂度，而不是一次出队复杂度。

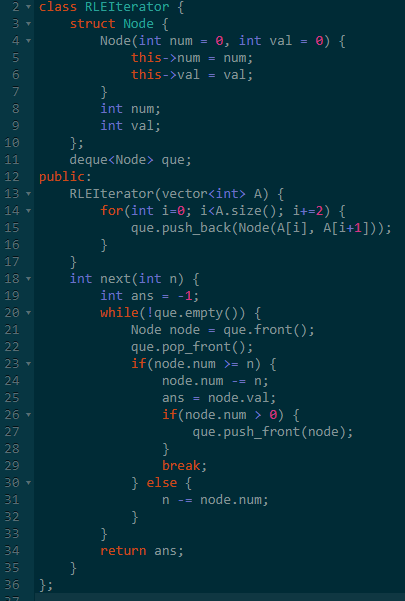
当然，我是使用双向队列实现的，使用数组一样可以实现的。

三、股票价格跨度

题号：901
题目：Online Stock Span
题意：每天输入一个数字，代表当天股票的价格，求每天股票的跨度。
定义股票的跨度为股票价格小于或等于今天价格的最大连续日数（从今天开始往回数，包括今天）。

股票的天数有10000次，所以我们不能想着分别循环求每天的股票跨度。

那这时候就要分析这道题的特征了，尤其是今天与昨天相比有什么特征。

假设今天比昨天的股价低，则今天的跨越度就只能是一天了。
而今天比昨天的股价高，则今天的跨度肯定包含昨天的跨度的，即我们直接从昨天跨度的前一天开始判断。
大概如下图的样子。

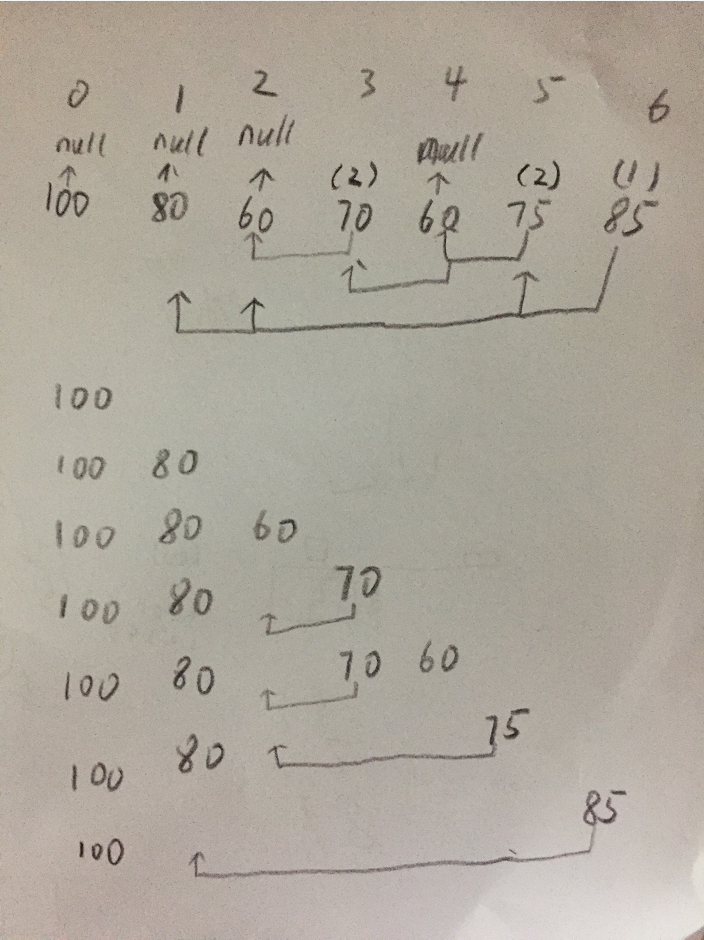
是不是有点KMP中next数组的味道？
这个思想的专业名称叫做单调队列。
所以我们就没必要为维护pre指针了，直接使用栈即可解决（参考上图的下半部）。

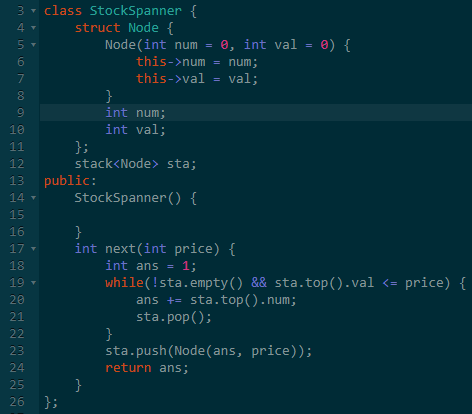
四、最大为 N 的数字组合

编号：902
题目：Numbers At Most N Given Digit Set
题意：给一个集合，他是1,2,3,4,5,6,7,8,9集合的子集（不包含零），求小于等于N且由集合里元素组成的数字有多少个。

例如对于1,3,5集合以及N=20的条件，可以组成数字1,3,5,11,13,15六个数字，所以答案是6。

面对这个问题，我们可以发现满足条件的数字分两部分：位数小于N的位数 与 位数等于N的位数。
对于位数小于N的数字，我们可以任意从集合里挑选数字，所以对于集合大小为k，位数为p数字有k^p个。
所以位数小于n=bit(N)的数字个数为k^1 + k^2 + ... + k^(n - 1)

而对于位数等于n的数字，则分两种情况：当前位的值与N相同 与 小于N当前位的值。
小的当前位值时，之后的位数随便选，而等于当前位的值时，之后的位数待确定。
具体代码如下，逻辑还是比较清晰：

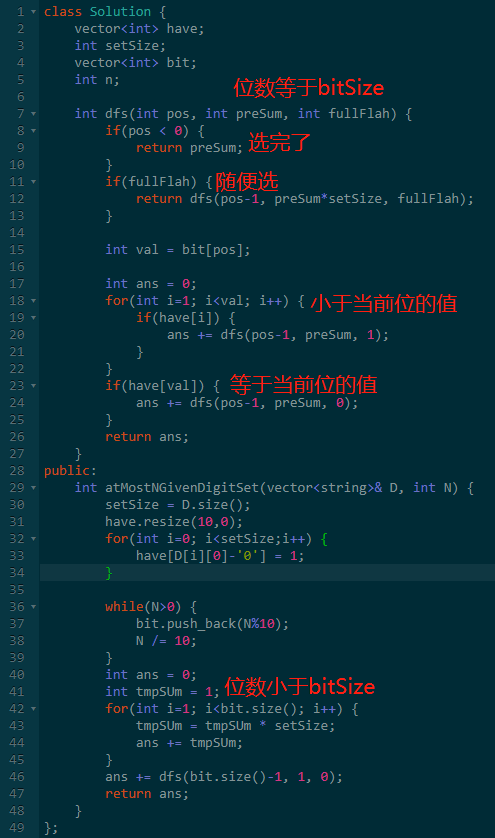
五、DI 序列的有效排列

编号：903
题目：Valid Permutations for DI Sequence
题意：有n+1个数字分别是0,1,2,...,n，然后给n个规则代表相邻位置的关系，求满足规则的排列个数。
规则具体分两种情况：一种是D代表前面的数字比后面的数字大，I代表后面的数据比前面的数据小。

简单的说就是给n个互不相同的数字，求所有满足给定上升和下降规律的排列个数。

比如，规则为DID，数字为0,1,2,3满足规则的排列有五个，分别是

(1, 0, 3, 2)
(2, 0, 3, 1)
(2, 1, 3, 0)
(3, 0, 2, 1)
(3, 1, 2, 0)

面对这道题，我们首先想到的是搜索，但是复杂度貌似太高。
状态压缩也有200多位，压不了。
使用容斥的话，发现容斥自身又用到了问题的答案。
最终我确定这个是一道动态规划题，但是有一个关键问题：状态怎么转移，怎么证明其正确性。

换句话说就是，当前问题怎么由子问题转化得到。
比赛的时候，我想了半个小时，一直在纠结假设前面i个数字是一个排列，怎么转化为i+1个，并且个数不重复也不漏。
最后比赛结束也没想出来。

赛后，我看了很多解题报告，想了好久，终于想明白了。
原来，大家都是直接说结论的，而我一直在对结论的正确性有疑问：怎么证明这个结论是正确的呢？
现在我就尝试使用一种容易理解的方式来讲解吧。

定义：dp[i][j]为0~i这些元素以j为结尾的合法的排列数。

如果正向看，假设所有的dp[i-1][0~i-1]都已经计算出来了，我们要求dp[i][j]。
假设此时规则是D，即最后一个位置的数字小于前面的数字。

那么对于任意满足dp[i-1][k]，k>=j的排列，将排列里面值大于等于j的元素都加1。
此时这些排列依旧满足前面的规则，而且最后一个位置的值将大于j， 即k>=j => k>j。
再将j放在这些排列的最后面，组成的新排列将会满足长度为i的规则。
上面说的排列的个数是dp[i-1][j] + dp[i-1][j+1] + ... + dp[i-1][i-1]。

现在有一个问题：怎么证明上面构造出的数列就是答案呢？ 会不会漏呢？

对于证明答案对不对，这个其实最好证明了。
因为只要找到一个反例，即可证明是错的。
所以证明方法就是反证法。

假设dp[i][j]存在一个反例数列，假设是A。
这个数列不是由dp[i-1][j], dp[i-1][j+1], ..., dp[i-1][i-1]中的某一个构造得到。
此时A的数字由0~i组成，j为结尾。

由于最后一个规则是D，所以A的倒数第二个数字k比j大。
此时我们删除最后一个元素，并将A里面所有大于j的数字减一，就可以得到一个以k-1为结尾且满足条件的数列。
由于k>j，所以k-1>=j，所以得到的这个数列在上面的构造集合里面。
因此假设不成立，证闭。

这个构造方法得到证明后，我们也可以很快的推理出I规则的构造方法。
对于I规则，不需要减一，直接将j追加在所有0~j-1为后缀的数列上即可。
大家可以证明一下其正确性。

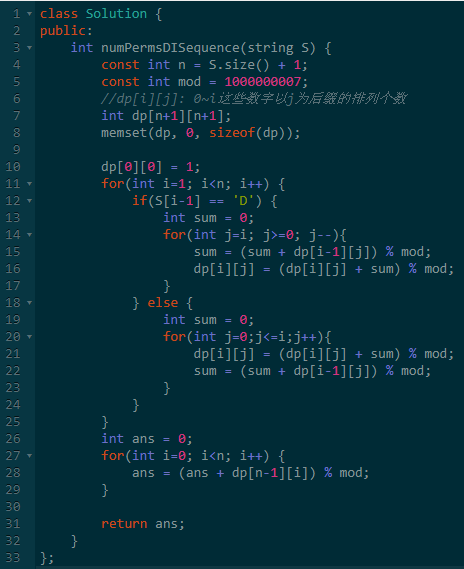
这样下来，代码就会很简单了。
默认这样做的复杂度是O(n^3)。
由于涉及到求前缀和 和 后缀和，这里代码稍微调整一下，即可累计使用之前算过的前缀或者后缀。
因此复杂度可以优化到O(n^2)。

六、最后

这次比赛涉及到的知识也比较多，如单调队列、dfs、dp。

对于单调队列，即使大家没听过这个名词，也可以自己想出类似的方法。

而对于dfs数字题，使用循环递推也是可以做出来的，只是需要考虑的边界情况比较多。

而对于dp，这次真的有难度，不能直观的想出答案来。
甚至告诉你答案，你也不明白。只有使用反证法证明了之后，我们才能确定这个动态转移方程确实是对的。
但是想要直接想到这个动态转移方程，确实不容易，反正我是没想出来。

另外。这次比赛，第一次在leetcode上前两道题那样的题型：互动式题。
而我的模板还不支持互动式题型，所以我计划再次更新一下我的Leetcode模板。

-EOF-