【算法】Leetcode 第129场比赛回顾

一、背景

之前已经写了几场比赛记录了，如第88场、第101场、第126场、第127场、第128场比赛。
今天上午我做了第129场比赛，现在记录一下题解吧。

PS1：今天的比赛时间比以往来的更早了一些，竟然提前一个小时开始了。
PS2：这次先分享第一题、第三题、第四题，最后分享第二题。
PS3：这次比赛题目的难度分级有很大的问题，尤其是第二题。

二、将数组分成和相等的三个部分

题号：1020
题目：Partition Array Into Three Parts With Equal Sum
地址：https://leetcode.com/problems/partition-array-into-three-parts-with-equal-sum/
源码：https://github.com/tiankonguse/leetcode-solutions/blob/master/contest/129/A.cpp

题意：给一个数组，求分成能否分成三个连续的子数组，使得三个子数组的和相等。

之前做过类似的题，不过那道题是判断是否存在一个连续的前缀子数组，其和等于指定的数字。
前缀子数组定义为这个子数组数给定数组的前缀，也就是前一部分组成的数组。

对于前缀子数组问题，一层循环累加即可判断是否存在答案。
而对于三个连续子数组，则可以转化为前缀子数组问题。

当然，转化前，我们需要先判断是否存在答案，即总和sum是否是3的倍数。
存在答案了，则子数组的和minsum也就确定了，都是sum的三分之一。

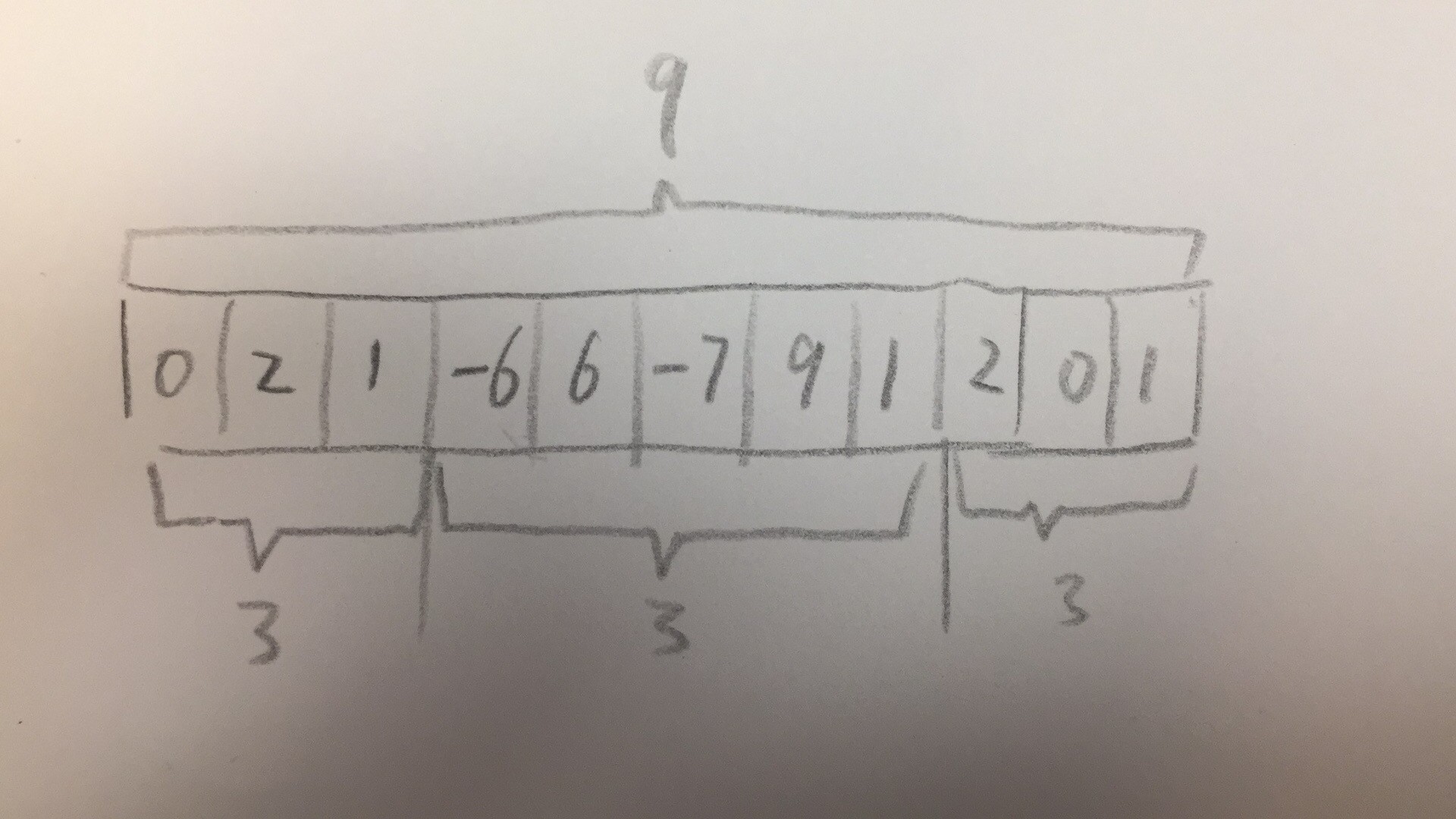
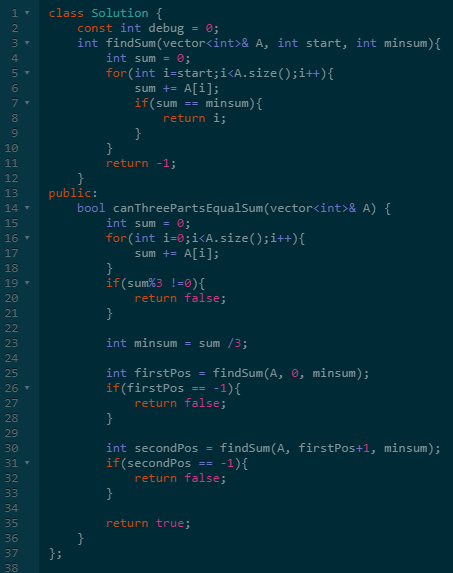
之后先找到第一个前缀子数组，然后找到第二个，则存在答案，否则不存在。

第一个很好求，对于第二个，只需要从第一个子数组之后开始查找即可。

三、最佳观光组合

题号：1021
题目：Best Sightseeing Pair
地址：https://leetcode.com/problems/best-sightseeing-pair/
源码：https://github.com/tiankonguse/leetcode-solutions/blob/master/contest/129/C.cpp

题意：给一个数组，任意挑两个位置(i, j)，其得分是A[i] + A[j] + i - j，求最大得分。
数据范围：[2, 50000]

这道题最先想到的是暴力的方法，但是复杂度是O(n^2)，肯定会超时。
所以我们就想能不能更快的解决这个问题，比如O(n log(n))或者O(n)。

如果向O(n log(n))的解决问题，那么问题可以转化为：对于每个j，我们可以二分查找找到前面的最优答案i。
此时我们把公式转化一下，j的值固定，是A[j]-j；i的值是A[i] + i。
而我们的目标是找到最大的A[i]+i。

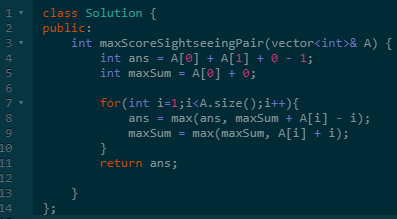
此时，我们可以发现，根本不需要二分了，对于每个i，公式A[i]+i都是固定的。
即令maxPre(n) = max(A[i] + i), 1<=i<=n
则maxPre(n+1) = max(maxPre(n), A[n+1] + n+1)。

我们扫描一遍即可找到所有j之前的max(A[i] + i)。

四、子串能表示从 1 到 N 数字的二进制串

题号：1023
题目：Binary String With Substrings Representing 1 To N
地址：https://leetcode.com/problems/binary-string-with-substrings-representing-1-to-n/
源码：https://github.com/tiankonguse/leetcode-solutions/blob/master/contest/129/D.cpp

题意：给一个二进制串S和正整数N，问所有小于等于N的数字对应的二进制是否都是S的子串。
数据范围：字符串长度[1,1000]，N的范围[1,10^9]。

看到N的数据范围，我们肯定不能枚举所有小于等于N的数字了。

但是考虑到，小于等于N的数字对应的二进制串是互不相同的 而我们的二进制子串最大有1000*(1000+1)/2个。
当N大于二进制子串总个数时，肯定是没有答案的。

所以到这里，N的数据范围就变成了[1, S^2]，令S = 1000。

此时枚举小于等于N的数字，然后判断是不是子串就可行了。

此时，暴力查找子串的话，复杂度就是O(S^2 * S * log(N))。
查找子串可以使用KMP优化，则复杂度变成了O(S^2 * S)。
由于子串是多次查询的，此时也可以使用字典表前缀树来优化，则复杂度是O(S^2 * log(N))。

前面是枚举所有的整数，由于整数一个都不能少，所以复杂度比较高。
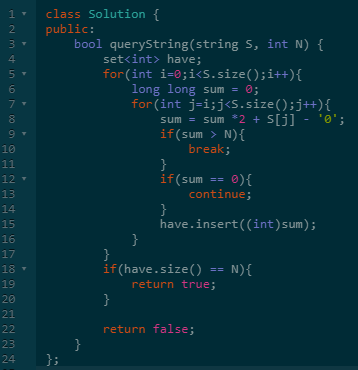
而我们枚举所有的子串，并统计得到不同整数的个数的话，如果有答案，则个数肯定等于N。
此时复杂度则降为O(S * log(N))，算是最优了。

五、可被 K 整除的最小整数

题号：1022
题目：Smallest Integer Divisible by K
地址：https://leetcode.com/problems/smallest-integer-divisible-by-k/
源码：https://github.com/tiankonguse/leetcode-solutions/blob/master/contest/129/B.cpp

题意：给一个正整数K，判断是否存在一个整数N，N的十进制数字全是1，并且N可以正整除K，即N%K=0。

这道题转化一下就是，给一个K，存在一个数A，使得A*K == N，且N满足条件。

面对这道题，想到的第一种方法就是搜索出满足答案的数字A。
首先，我们可以确定K的个位只能是1,2,7,9，因为其他数字和任何数字相乘各位都不是1。

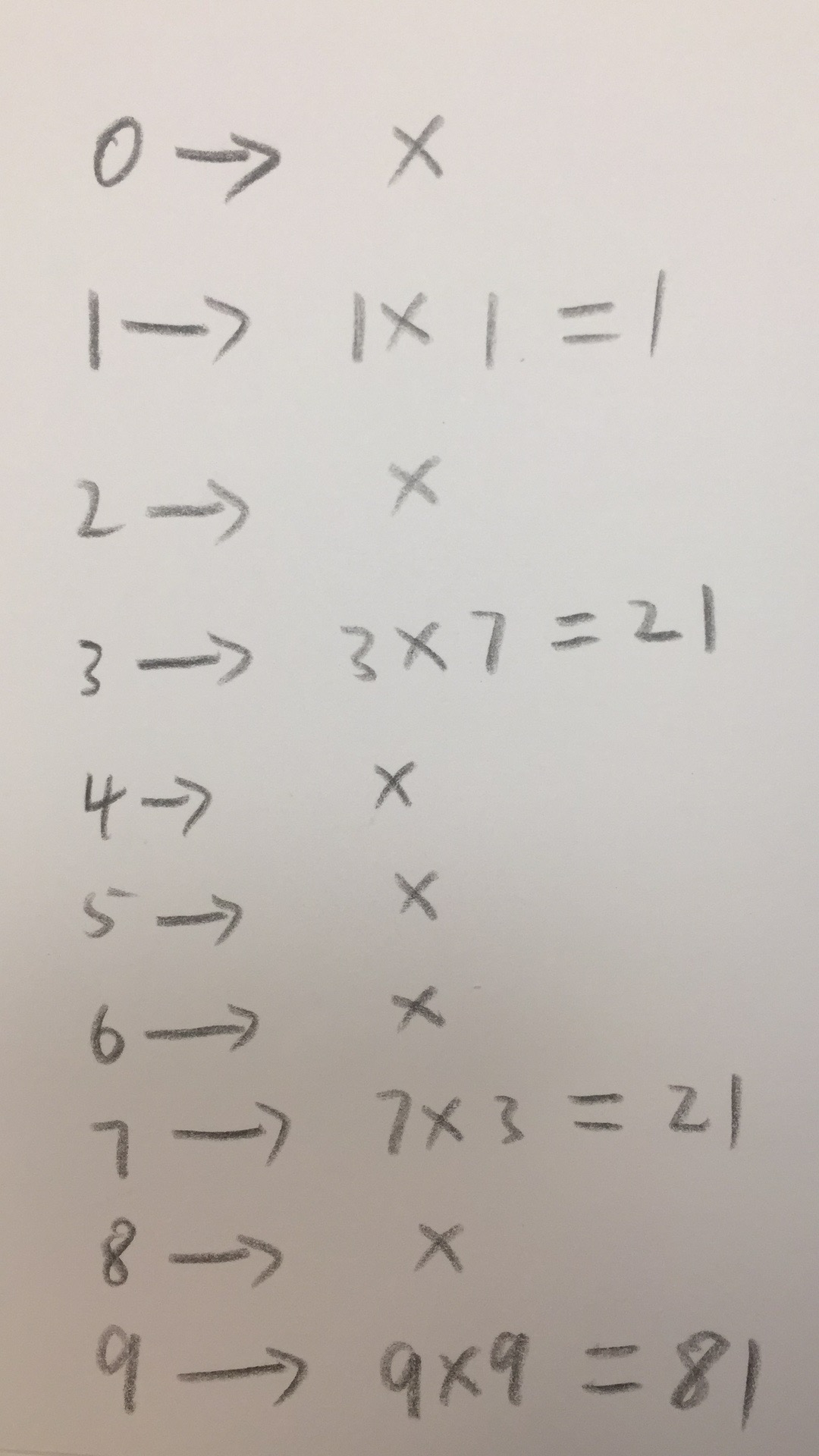
其次对于答案A的个数数字，可以根据K的个位数字k0来唯一决定了。
因为其他数字与任何数字相乘，不能得到个位是1的乘积来。
例如K的个位是3，则A的个位只能是7，其他的都不能得到数字1。

到第二位时，就变得复杂了。
因为有进位，我们不再是得到1，而可能是任意数字，但这个数字根据之前的计算可以唯一确定。
使用公式表达就是求一个数字p，使得(k0 * p + preSum)%10 == 1。

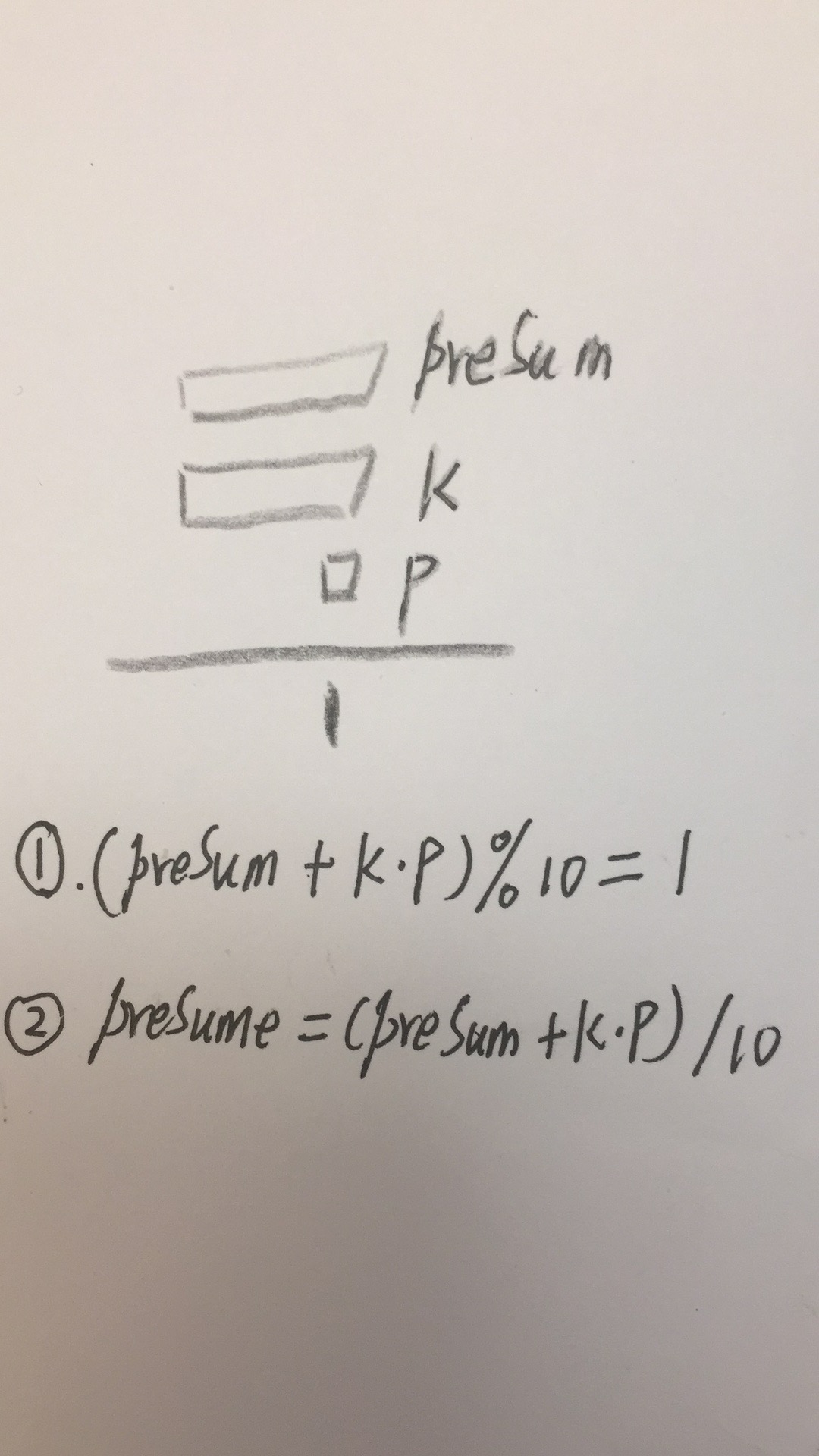
公式转化一下，就是(k0 * p)%10 == (11 - preSum%10)%10。
此时，可以里利用上面计算的映射表，实现一个dfs来找到答案。
但是有一个致命的问题：dfs如果不能终止怎么办？

不管那么多了，先提交再说。
暴力搜索竟然过了，当然，这个是在结束比赛的时候提交的。

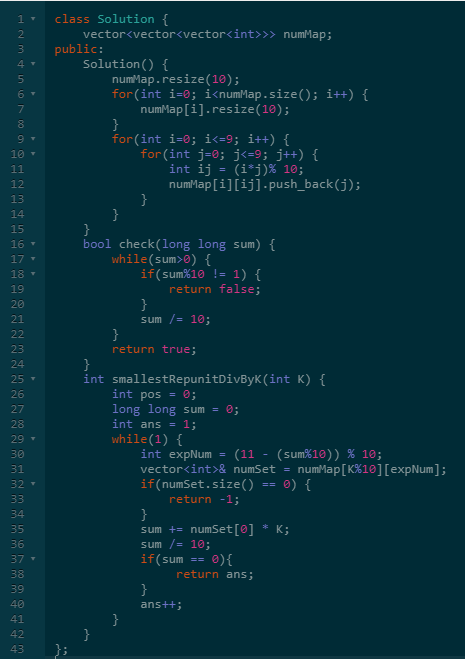
既然暴力搜索可以过，代表一定存在答案，那反过来，枚举1的个数应该也可以过。
假设sum是答案，且sum由sum0 * 10 + 1组成。
因为sum%K == 0，所以我们可以推出(sum0%K * 10 + 1)%K == 0。
所以累计计算的时候，需要不断的模K防止sum越界。

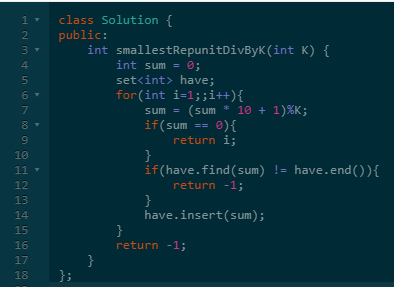
那接下来的问题是：为什么？
怎么证明答案一定可以在O(n)的复杂度计算出来。

这个还是需要看我们的暴力搜索逻辑。
面对关键的方程式preSum = (preSum + K*P)/10，假设其是收敛的，我们可以证明最多在K次循环内可以收敛到0。

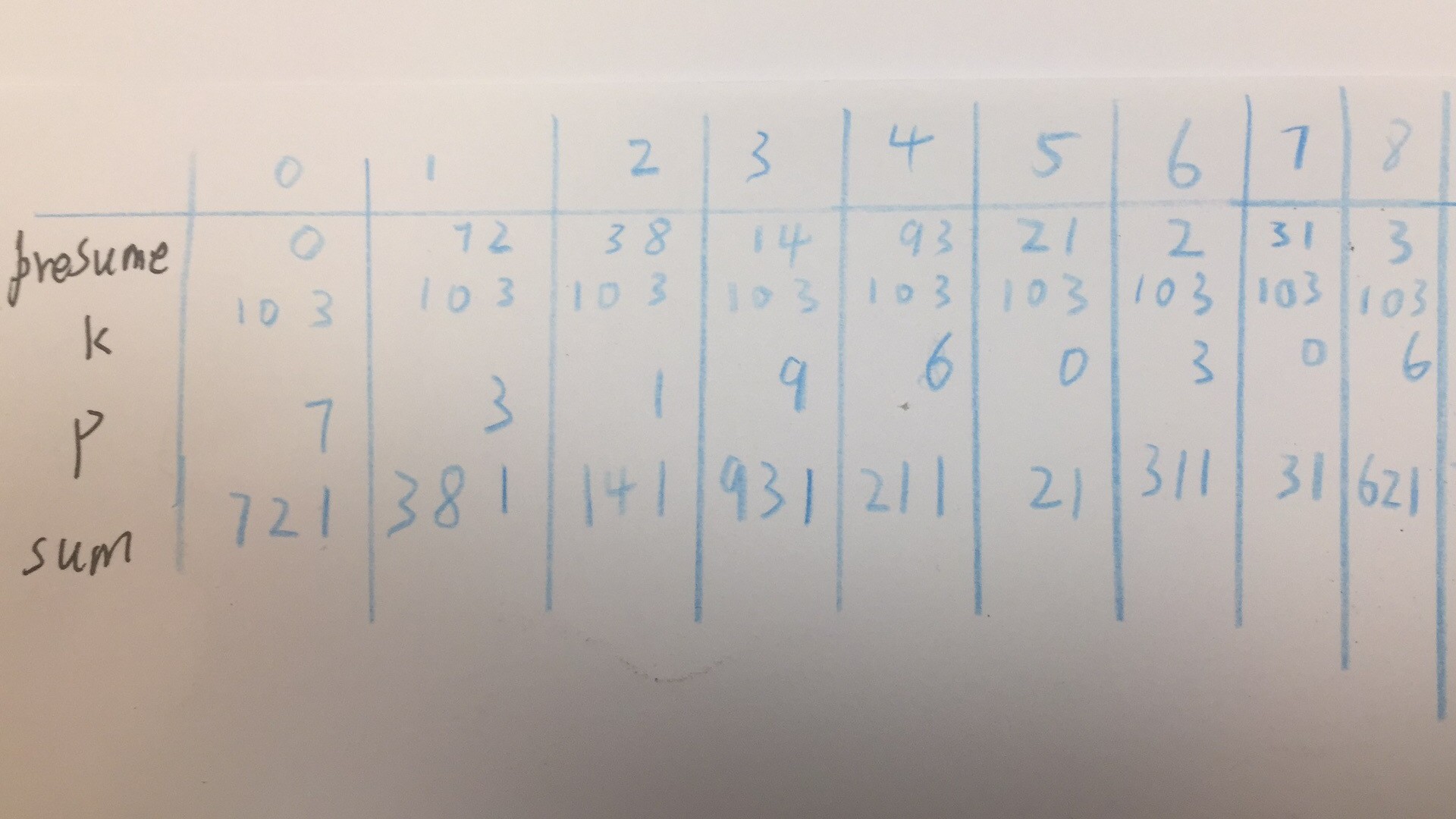
大家可以看上图，每次计算其实只与preSum 有关，我们可以证明preSum肯定小于K。
证明如下：
前提preSum0=0 < k，0 <= p <= 9
零、preSum1 = (preSum0 + k*p)/10 一、preSum0 + k*p < k + p*k
二、preSum0 + k*p < 10*k 三、(pre + k*p)/10 < k
四、preSum1 < k

前面是假设收敛可以证明循环有限，有限了就可以找到答案。
那假设不成立呢？即会不会形成死循环，从而不会收敛。
例如 preSum计算若干次后，又回到了自己这个值。

这时候还需要分析preSum1和preSum的关系了。
我们知道，preSum可以唯一的推出preSum1，那逆着会怎么样呢？
经过简单计算，发现这个公式是可逆的，而且逆向的preSum也是唯一的。

此时假设有环，则肯定指向第一个preSum即等于0，也代表找到答案。
所以这里就证明了，在找到答案之前，是不可能形成死循环的。

这里的必然存在答案是使用preSum1和preSum的关系证明。
那有没有数学的证明公式呢？
还真有！

定义bit(n)代表n个1组成的数字。
假设bit(1) ~ bit(k)都不能整除k，则他们模k后属于集合[1,k-1]。

根据容斥原理，肯定有两个数字取模到一个余数了，假设是bit(i)与bit(j)。
即bit(i)%K == bit(j)%K
调整一下顺序，可以得到(bit(i) - bit(j))%K == 0。

由于bit(x)的位置上全是1
可以得到bit(i)-bit(j) = bit(i-j)*10^(j)。
也就是前面有i-j个1，后面有j个0。

由于(bit(i) - bit(j))%K == 0
我们可以得到bit(i-j)*10^(j) % K == 0
由于K的个位是1,3,7,9其中一个，所以K不可能是2和5的倍数。
进而得到10与K互质。
因此bit(i-j)%K == 0
假设不成立，因此1~k内存在答案。

看到这里，其实我们一直在证明如果K的个位是1,3,7,9时，循环K次肯定可以找到答案。
也是就是证明，这道题在O(k)复杂度内可以计算出来。

那有没有更优的算法呢？
还是看题目：求最小的n使得bit(n)%K == 0。
扩大9倍可以得到：9*bit(n) % (9K) == 0
转化为10的倍数可以得到(10^(n+1) - 1) % (9K) == 0
即10^(n+1) % (9K) == 1

这个就是经典的欧拉问题了。
通过欧拉函数，我们可以在O(sqrt(n))复杂度内计算出答案。
由于我们计算的是9K的欧拉函数，而对于K，之间的关系又是确定的（这里不证明）。
即答案是9K欧拉函数的其中一个约数。
这个可以枚举所有约数来找到
综合复杂度O(sqrt(n))

六、最后

这次比赛很坑。
第二题的难度实际上属于hard的，缺标记为medium，并放在第二个。

比赛的时候，10分钟做完第一题，第二题做了40分钟，一直在纠结会不会死循环。
后来看时间不够了，赶紧做第三题和第四题，发现是水题，就赶紧过了。
剩余的时间就都耗在第二题了。

另外，我的leetcode模板根据使用的体验，准备做一个较大的优化。
模板地址：https://github.com/tiankonguse/leetcode-solutions/tree/master/include

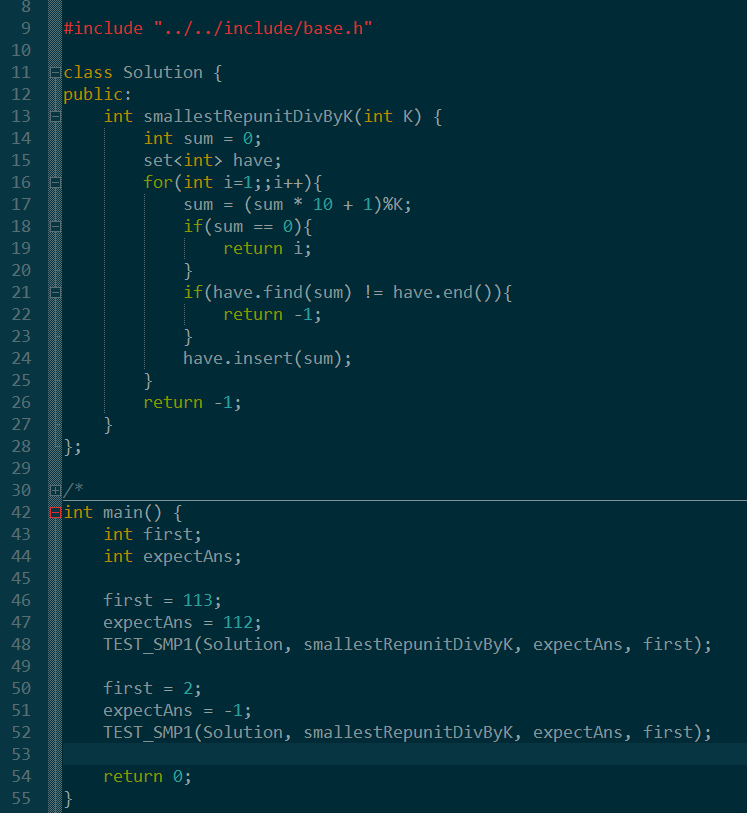
具体优化即使不需要编写test函数了，已经使用宏封装好了。
另外，头文件等与题无关的代码都移动到了base.h里面去了。

-EOF-