【算法】Leetcode 第130场比赛回顾

一、背景

发现一个Leetcode的一个重大秘密，偷偷告诉你。

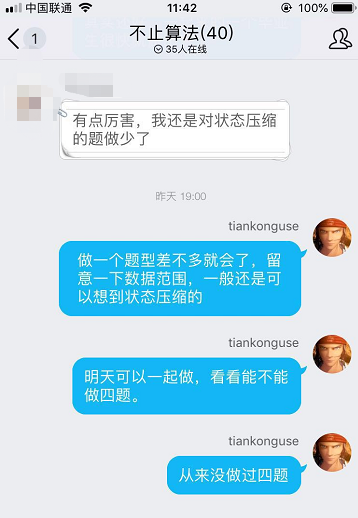
leetcode这次举办比赛的官方人员肯定监听我的QQ算法群的聊天记录了。
我昨晚才在群里说我比赛从来没做过四题，每次都是三题。
然后今天比赛他们就放水了，给了我一次机会。
按照国人的逻辑，这个是实锤的事情了。

好了，下面来看看这次比赛 Leetcode 是如何放水让我做出四道题的吧。

二、可被 5 整除的二进制前缀

题号：1029
题目：Binary Prefix Divisible By 5
地址：https://leetcode.com/contest/weekly-contest-130/problems/binary-prefix-divisible-by-5/
源码：https://github.com/tiankonguse/leetcode-solutions/blob/master/contest/130/A.cpp

题意：告诉你一个0和1组成的二进制字符串，判断所有的前缀二进制串是否可被5整除。

思路：由于是求所有前缀的答案，那扫描一遍，计算出所有前缀的十进制数字，判断即可。
这里有个注意事项时，十进制数字可能很大，需要边计算边取模。

关键思想与原理如下：

pre(i) = pre(i-1)*2 + val[i])
  pre(i) % 5
= (pre(i-1)*2 + val[i])%5
= (pre(i-1)% 5)*2 + val[i])%5

class Solution {
public:
    vector<bool> prefixesDivBy5(vector<int>& A) {
        vector<bool> ans;
        int now = 0;

        for(int i=0; i<A.size(); i++) {
            now = (now * 2 + A[i])%5;
            if(now ==0) {
                ans.push_back(1);
            } else {
                ans.push_back(0);
            }
        }
        return ans;
    }
};

三、负二进制转换

题号：1028
题目：Convert to Base -2
地址：https://leetcode.com/contest/weekly-contest-130/problems/convert-to-base-2/
源码：https://github.com/tiankonguse/leetcode-solutions/blob/master/contest/130/B.cpp

题意：对于二进制，大家没有疑问，公式是2^0 + 2^1 + 2^2 + ...。
那负二进制，就是-2的公式：(-2)^0 + (-2)^1 + (-2)^3 +...
给你一个数字N，求其-2进制。

思路：首次看到这道题时，我是一脸懵逼的。
第一个疑问是：这样能表示所有的数字吗？

于是在纸上随便举了一个例子，发现真的可以。
发现真的可以时，也找到几个特征。

特征一：二进制的公式里，正负符号是相反的。
特征二：如果在正常的二进制位置上符号为正时，可以使用更高位减去当前位得到答案。
例如：假设第2k+1位在正常二进制应该是1，但是在负二进制里基数是-2，我们计算的结果是(-2)^(2k+1)。
我们的目标是求2^(k+1)。
那我们给整个二进制加上(-2)^(2k+2)即可得到目标。

推理如下：

 (-2)^(2k+2) + (-2)^(2k+1)  
=2^(2k+2) - 2^(2k+1)  
=2*2^(2k+1) - 2^(2k+1)  
=2^(2k+1)  

既然这样，我们只需要模拟大整数加法，遇到需要加2^(2k+2)时，进一位即可。

string baseNeg2(int N) {
    if(N == 0){
        return "0";
    }
    string ans;
    int pre = 0;
    int bit = 0;

    while(N>0 || pre >0){
        int sum = N%2 + pre;
        if(sum == 0){
            ans.push_back('0');
        }else if(sum == 1){
            ////根据奇偶性决定是否进位
            pre = bit%2;
            ans.push_back('1');
        }else if(sum == 2){
            pre = 1; //进位
            ans.push_back('0');
        }
        bit++;
        N = N/2;
    }

    std::reverse(ans.begin(), ans.end());
    return ans;
}

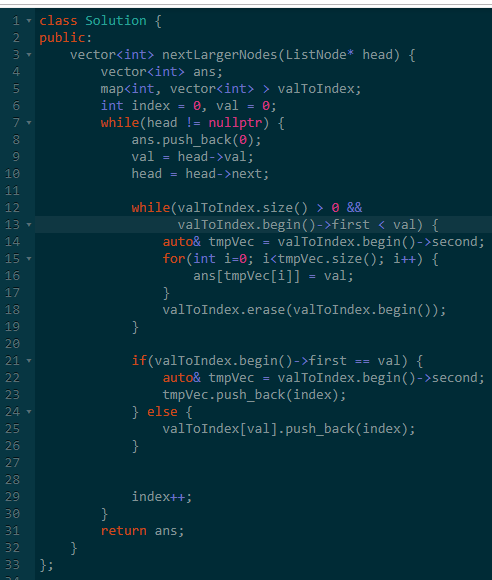
四、链表中的下一个更大节点

题号：1030
题目：Next Greater Node In Linked List
地址：https://leetcode.com/contest/weekly-contest-130/problems/next-greater-node-in-linked-list/
源码：https://github.com/tiankonguse/leetcode-solutions/blob/master/contest/130/C.cpp

题意：给一个链表，求出每个节点之后第一个大于当前节点的值。

思路：由于是求之后第一个大于的值，很容易发现有一个特征。
特征：零i<j且val[i] >= val[j]， 我们可以证明，任何时候i都比j更优。
具体意思就是，对于i前面的数字，如果在i和j里面选择一个答案的话，我们只能选择i。

这个思想其实单调队列，前面的比赛已经提到无数次了。

所以第一种方法就是：逆序遍历序列，维护一个单调队列即可。

但是，当我敲代码的时候，发现输入的是链表。
那好办，先把链表转换为数组即可。

那有没有直接扫描链表就得到答案呢？
还真有。

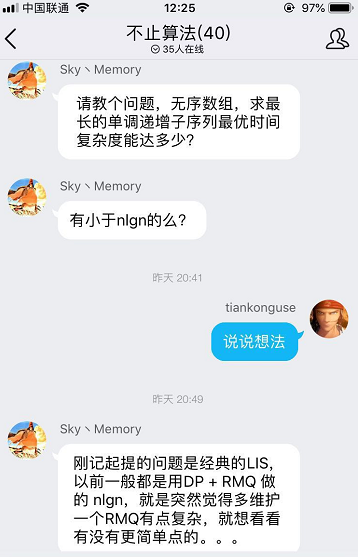
恰好在昨晚，在我的不知算法QQ群里，有人问最长递增子序列有比n log(n)更优的算法吗？
我问他的想法时，他说记得可以使用DP+RMQ优化到n log(n)。
我想了想，认为只需要使用单调队列优化即可达到n log(n)。

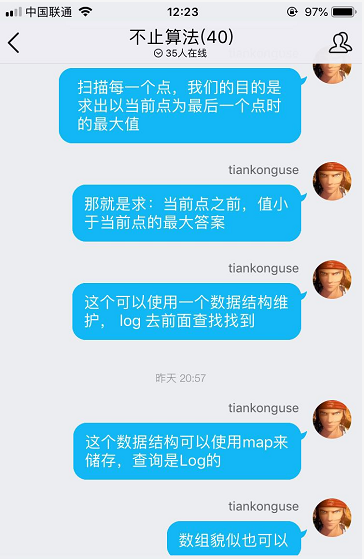
随后我也给出了其严格的证明推理，为什么会更优。

面对这种题型，如果使用数组储存的话，我们称为单调队列。
其实，也可以使用map储存的，思想依旧是单调队列。

既然可以使用map储存，我们就可以从前到后扫描了。
只不过相反，这里扫描到一个点时，是为了寻找这个点时前面那些点的答案。

假设我们维护了这样一个数据结构：全是还知道答案的点。
扫描到一个位置时，数据结构里面，比这个位置小的点的答案 全是这个位置。
然后更新数据结构：删除已经找到答案的点，然后当前位置加入数据结构。

PS：这里有一个注意事项：位置的值可能重复，所以值相同时，所有的下标都需要保存下来。

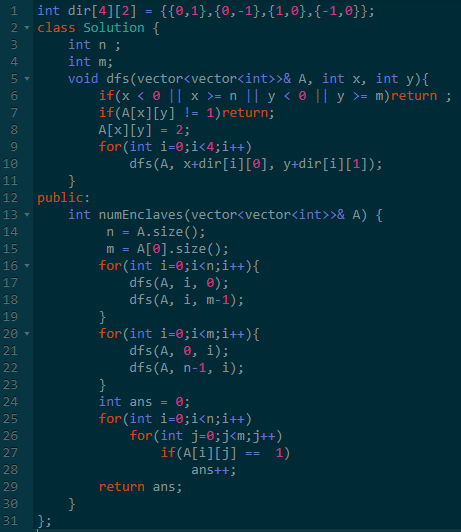
五、飞地的数量

题号：1031
题目：Number of Enclaves
地址：https://leetcode.com/contest/weekly-contest-130/problems/number-of-enclaves/
源码：https://github.com/tiankonguse/leetcode-solutions/blob/master/contest/130/D.cpp

题意：给一个地图：海与陆地，询问没有和边界相连的陆地的个数（孤岛）。

思路：大水题，一个DFS或者BFS即可。

正常思路是遍历每个点，当前点未访问过时，开始搜索。
如果发现了边界，将搜索的所有点都标记为非孤岛。
如果未发现边界，将搜索的所有点都标记为孤岛。
最后计数即可。

比较优秀的思路是直接扫描四个边界，就行搜索标记。

注意事项：每个点只能递归搜索一次，搜索之后，就应该标记为访问过，后面不能在访问，否则复杂度将是O(n^4)。
复杂度：O(n^2)，其实就是地图的大小。

六、最后

这次比赛，涉及到了两道数学题、一个单调队列题、一道搜索题。
都是较为基础的题，大家可以练习一下。

-EOF-