【算法】栈DFS就是这么简单

一、背景

之前写了五篇文章来讲解了《数组就是这么简单》系列，前天写了一篇文章来讲解《队列就是这么简单》，昨天用一篇文章来介绍《栈理论就是这么简单》，今天来看看《栈DFS就是这么简单》吧。

理论知识

前面的文章我们知道了，栈是一种后进先出的数据结构。
通过栈能够实现深度优先搜索，从而可以用来解决树、图、以及搜索上的问题。

对于图，搜索顺序如下图：
起始节点先入栈。

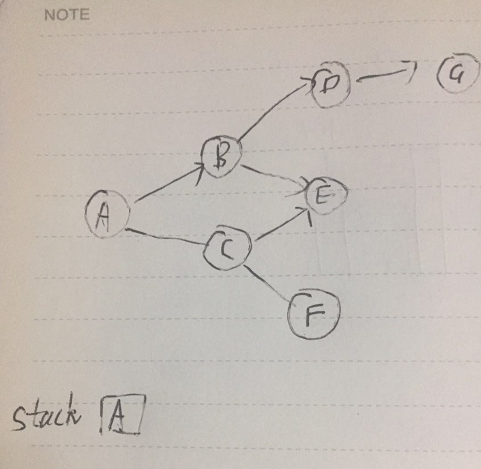
然后找选择一个子节点路径，直到尽头。

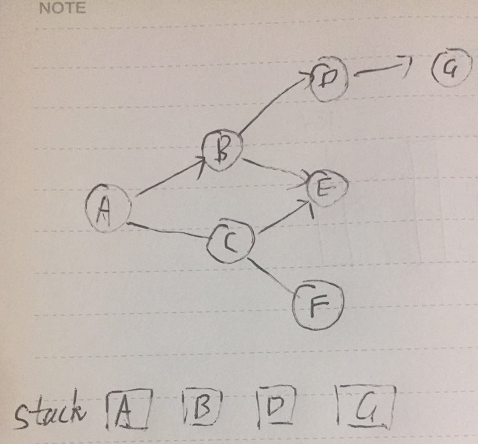
接着，当前路径的最后一个节点G处理完成后，会尝试扫描倒数第二个节点D的其他儿子。
当倒数第二个节点的所有儿子处理完后，会尝试扫描倒数第三个节点B的其他儿子。
如下图，路径变成了A->B->E。

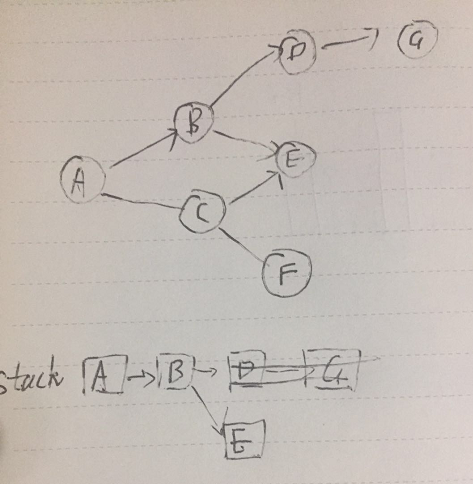
接着,B的所有儿子处理完了，就要回溯到A，然后处理A的其他儿子。
这样就进入了路径A->C->F了。
这路需要注意的是，E节点我们已经处理过了，所以我们不会生成A->C->E路径。

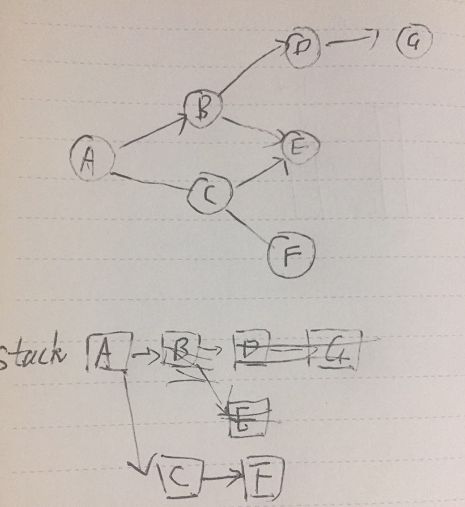
这样，我们就模拟了深度优先搜索DFS的过程，搜索过程中，父节点的信息保存在栈中，从而能够完成回溯搜索。
当然，上面的模拟过程为了简单，省略了一些东西。

实际使用的时候，如果一个父节点遍历了子节点（遍历后代表当前节点处理过），我们不会储存在栈中。
栈中实际储存的是尚未处理的节点信息。

另外，对于栈的使用有两种方法。
一种是自己使用数据结构栈来处理数据，一种是使用函数的递归形式来处理DFS相关的问题。
使用数据结构的好处是我们的栈可以很大，但是储存的信息有限。
使用函数递归的好处是我们可以保存一个节点的上下文，在计算完所有子节点的时候，可以聚合出一个结果来（具体见下面的实践题目：目标和），从而做到避免重复计算。

具体的实现可以看下面的实践代码吧。

三、岛屿的个数

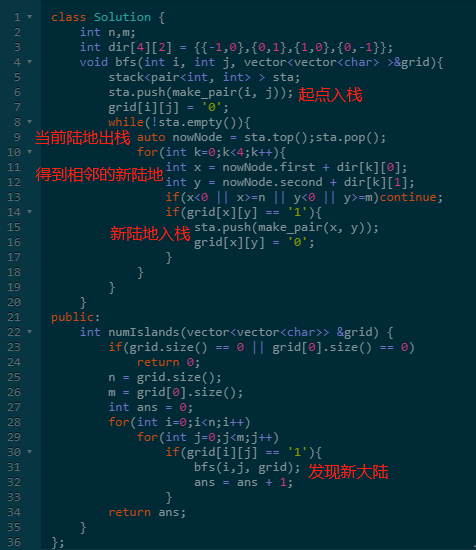
题意：输入一个二维数组，值是0海水或1陆地。陆地上下左右方向挨着时代表陆地连接着。
求互相独立的岛屿个数。

思路：如果你看过之前的文章的话，就会发现这道题之前做过了。
上次是使用队列把这道题解决了，现在需要使用栈来解决。

思路则是每次将相邻的尚未处理的陆地加入到栈中，然后依次处理。

四、克隆图

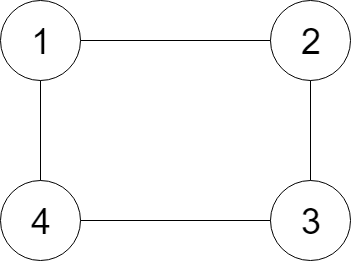
题意：给一个无向连通图（指针），求深拷贝该图。

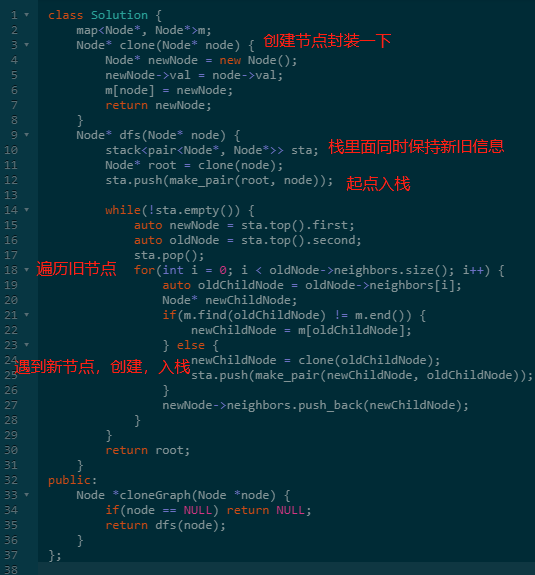
题意：这里除了要正常的递归外，还涉及一个问题：如何找到一个节点的指针。
这个使用map储存起来即可，由于不知道val是否重复，储存指针的映射关系最靠谱。

五、目标和

题意：给定一个非负整数数组和一个目标数，我们可以给每个数赋予一个符号，问最终数组和等于目标数的个数。

思路：假设有N个数字，每个数字有两个符号，则共有2^N中组合情况。
由于是求方案个数，我们需要遍历所有的组合情况。
所以问题转化为了：如何遍历组合数。

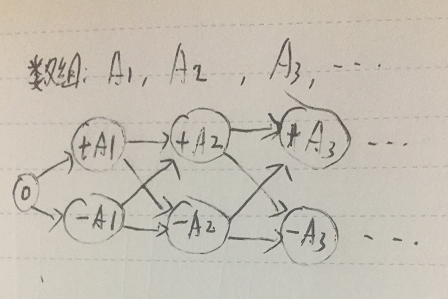
其实，对于组合问题，可以转化为图的遍历问题。
比如这道题可以转化为下图，起点是0，可以到达第一个数的两种情况，然后可以到达第二个数的两种情况，直到最后。

对于搜索问题，我们会发现有很多重复的搜索。
比如1 1 1 1 1这个数据，到达第三个位置的时候，路径和是1的情况有很多种。
比如

+ 1 + 1 - 1
+ 1 - 1 + 1
- 1 + 1 + 1

此时，去搜索第四个位置的时候，都是使用前缀和1在第四个位置上搜索。
这样我们就会重复搜索三次。
如果搜索第一次的时候，就记录下答案的话，后两次即可直接得到结果。

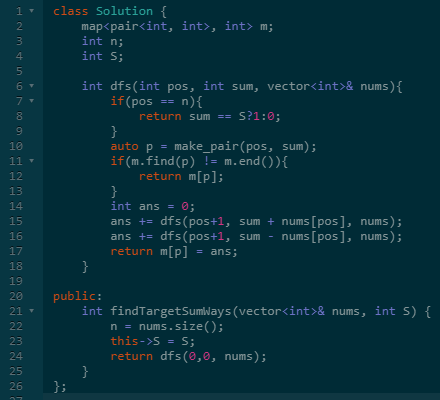
每个位置和前缀和组合起来才算一个状态，所以我们使用位置和前缀和来作为map的key。
具体参考下面的代码。

六、二叉树的中序遍历

题意：给定一个二叉树，返回它的中序 遍历。
要求：递归算法很简单，要求自己使用栈实现。

思路：先来看看递归的代码吧。

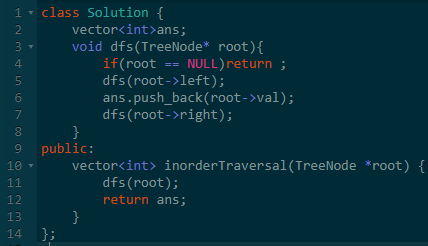
递归确实好简单，那自己模拟栈了的时候面临一个问题：我们不知道中间这个节点是首次出栈还是第二次出栈。

首次出栈的时候，我们需要找到左儿子。由于是中序，父节点还需要进入栈。
第二次出栈的时候，代表左儿子处理完了，父节点直接输出到答案里面，接着需要处理右儿子。

既然不知道，那就记录下来。
记录的这个其实就是上面提到的递归的上下文。

比如使用一个字段来表示状态，0代表首次出栈，1代表第二次出栈。
然后就可以写出和递归一样的代码了。

大家可以对比一下递归的实现和这个栈的实现。

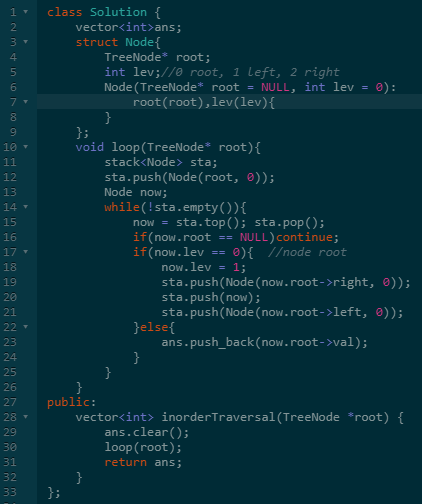
七、最后

这篇文章简单的介绍了栈的一些实践题。
由于函数递归就是一种系统栈，所以一般情况下我们都是直接使用函数递归的解决问题的。
而对于那些不需要父节点与子节点上下文关系的场景，我们直接使用栈来处理也很方便。
大家到时候可以按照这个上下文关系为指标，来决定是使用栈还是使用递归吧。

-EOF-