Leetcode第95场比赛回顾

零、背景

这周五团队一起做了 Leetcode 第 95 场比赛。
做到第二题，我就发现很多人可能到这里就不会了。
做第三题时，我刚开始完全没想法，是先跳过去做第四题的，最后有想法了才把第三题干掉的。
现在来看下比较有难度的一场比赛吧。

PS：这次比赛我是第一次直接在浏览器上做题的，没想到浏览器上敲代码这么方便。
正常比赛下来，只用了一点小时多一点。
明天又比赛了，我再尝试在浏览器上做题试试。

一、链表的中间结点

题号：876
题目：Middle of the Linked List
题意：输出链表的中位数。 如果有两个（偶数长度），输出后面那个。

思路：最简单的方法就是先循环求出链表的长度，计算出答案的位置，然后循环找到那个位置即可。
可以看到，这样需要循环两次才能找到答案。

另一种更快的方法是使用快慢指针，这样循环一遍就可以找到答案了。

二、石子游戏

题号：877
题目：Stone Game
题意：N堆石头排成一行，Alex 和 Lee 两个人轮流拿走一堆石头。
问最终第一个人Alex拿到的石头是否可以比第二个多。
规则：有偶数堆石头，每次只能从两头来选一堆。

思路：第一眼看到这道题，我们可以确定这是一道博弈题。

但是不能直接根据递归的子状态来判断是否能赢。
我们只能做到求出子状态的最优值，返回给当前状态，然后求出当前状态的最优值。

以p[1] p[2]... p[n-1] p[n]为例。
当前状态是1~n，Alex的目标是在1~n的两边选择一堆石头，使得自己的总石头数量最大，我们称为f(1,n)。

当Alex选择p[1]时，Lee肯定会尽使自己的石头数最大，即f(2,n)。
此时Alex的石头总数是sum(1,n) - f(2,n)。

当Alex选择p[n]时，Lee的选择则是f(1,n-1)。
此时Alex的石头总数是sum(1,n) - f(1,n-1)。

面对这两种选择，Alex肯定选择两个结果里最大的选择。

分析到这里，我们也就把这个博弈过程讲清楚了。
具体用代码实现就是一个 DFS。
而考虑到子状态存在重复计算，则需要记忆状态。
当然，这两个结合起来，其实就是动态规划了。

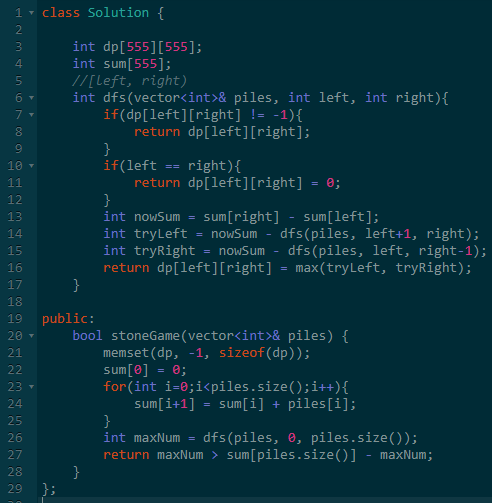
赛后，大家讨论的时候，一个同学说：我没找到Alex失败的情况，于是直接提交Alex永远成功，想看看反例是什么。结果提交后这道题就过了。
然后也有几个同学说自己的算法敲错了，最终也都过了。
那为什么会这样呢？

后来我想了想，想明白了为什么Alex必胜Lee必败。
而且道理也很简单，不信你看。

总共有偶数堆石头，石头总个数是奇数个。
这说明最终肯定有一个人胜出。

偶数堆按奇偶性分别求和，则要么偶数堆大，要么奇数堆大。
假设石头堆是1 ~ 2n。

如果偶数堆大，则Alex选择p[2n]这堆石头，Lee只能选择p[1]或p[2n-1]，即只能选择奇数堆。
之后Alex依旧是选择偶数堆，而Lee只能选择奇数堆。
最终，Alex选择的都是偶数堆，Lee选择的都是奇数堆，这样Alex就比Lee选的多了。

而对于奇数堆大，是一个道理。
所以第一个选择的人Alex必胜了。
这道题算是有史以来代码最短的题了，只需要return true;即可。

三、第 N 个神奇数字

题号：878
题目：Nth Magical Number
题意：如果正整数可以被 A 或 B 整除，那么它是神奇的。 返回第 N 个神奇数字。
规则：由于答案可能非常大，返回它模 10^9 + 7 的结果。

思路：看到这道题的第一眼，我是一脸懵逼的，于是就先做下一道题了。
下一道题做完后，只剩这一道题了，就只能分析这道题的特征了。
一分析不要紧，还真找到一个规律：神奇数是有周期的，周期就是 A和B的最小公倍数。

假设 A 和 B 的最小公倍数是 G，其中有 m 个神奇数，分别表示为f[1],f[2]...f[m]。
则第 m+1个神奇数肯定是 G + f[1]，而第 m + 2 个神奇数肯定是 G + f[1]。
推广就是，第N个神奇数是 G * (N/m) + f[N%m]。

那接下来的问题就是：怎么求最小公倍数以内的所有神奇数？会不会很多？会不会超时？
面对发自内心的三连问，我想先解决第一个问题：先写出代码提交了再说。
写了一个循环就求出了所有的神奇数，提交后就过了。

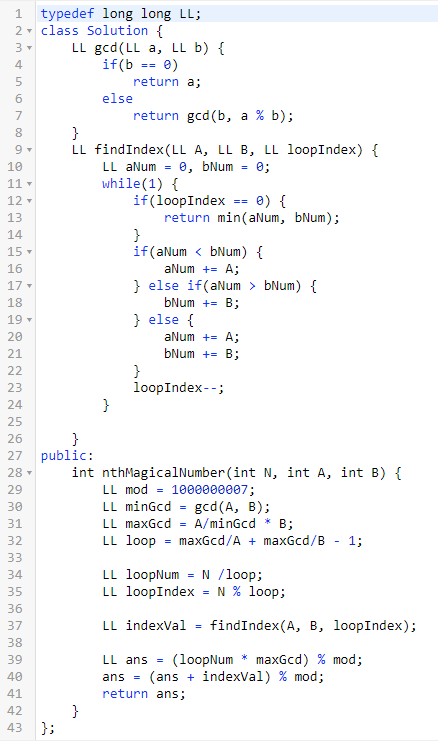
然后我思考：为什么没超时？会不会本来就不多？怎么证明？
面对接下来的三连问，其实是一个问题：怎么证明公倍数内的神奇数不多。
简单一思考，发现很容易证明。

与 A 有关的神奇数是A,2A,...,BA。
与 B 有关的神奇数是B,2B,...,AB。
这样合起来神奇数最多就是A+B-1个。
在考虑公约数的问题，神奇数还会比这个还少，即只有G/A + G/B - 1个。

而 A 和 B 只有几万，复杂度可以接受，所以这样做不会超时，证闭。

四、盈利计划

题号：879
题目：Profitable Schemes
题意：有 G 个人，有多起犯罪同时发生。
每个犯罪需要 group[i]个人，可以获取profit[i]的利润。
统计到犯罪至少获取的利润是 P,问可能有哪些犯罪发生。

思路：只要题意看懂，就可以看出这是一道基本的动态规划题，甚至是背包问题的变种。
直接把涉及到的变量组装起来，就可以表达出状态：f(G, P, n)。
含义是前n起犯罪里不超过G人时至少获得利润P的情况数。

此时对第n起犯罪分情况讨论。
如果参与犯罪（前提是能），则状态转化为f(G-g[n], P-p[i], n-1) + check(p-p[i])。
check的含义是到目前未知，利润是否已经够了，够了就算一个答案。
如果不参与犯罪，则状态是f(G, P, n-1)。

就这样，就可以求出答案来，复杂度O(n^3)

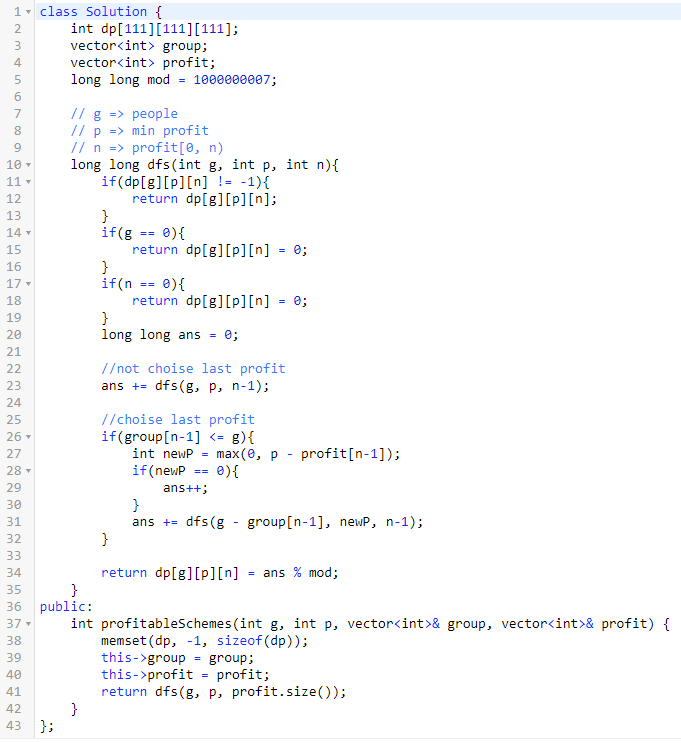
五、最后

这次比赛其实蛮有难度的。
除了第一题是水题，第二第四是动态规划，第三是数学题，一般人面对这三道题都会是一道坎。
除非你非常聪明，一般人都需要大量的训练才能熟练的掌握这些题型的。
当然，第二题其实不好，很多人代码敲错了都水过去了。刚才我看了下我的代码，有个地方敲错了，少了个逗号，也过了。

PS：最近我在想怎么把自己做过的题组织起来，以供大家搜索、分类，从而方便的进行专项练习。
目前的选择有两种，一种是在我的网站上实现这个功能，一种是使用知识星球的标签功能，大家怎么看这个呢？

-EOF-