初级算法实践之动态规划

一、背景

动态规划，很多人望而生畏的名词之一。

其实，动态规划只是一种思想。
即将现有问题拆分为若干子问题，分别求之，最后合并子问题的结果求出当前问题的答案。

在拆分子问题的时候，可能涉及到子问题的重复运算。
所以需要使用对子问题的计算结果进行保存，下次需要的时候直接返回结果即可。

这里涉及到两个关键点。

1.可以拆分为子问题，并由子问题的答案计算出当前问题的答案。
2.子问题的结果可以保存起来的。

有了这两个关键步骤，我们就可以解决大部分动态规划题了。

比如下面有四道动态规划题，你应该都可以学会。

二、爬楼梯

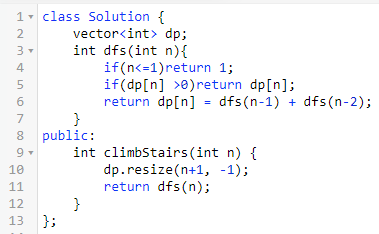
题意：有一个n层的台阶，现在你要从底部爬到顶部。
你每次可以爬一层，也可以爬两层。
问你有多少种不同的路径从底部爬到顶部。

思路：我们可以只看第n个台阶。
则第n个台阶可能由两个台阶到达，一个是第n-1个台阶，一个是n-2个台阶。

所以从底部到达第n个台阶的路径个数可以拆分为两类。
一类是从底部先到达第n-1个台阶，然后再到达第n个台阶。
另一类是从底部先到达第n-2个台阶，然后直接到达第n个台阶。

从底部到达第n个台阶我们用f(n)表示。
则上面的子问题可以由公式f(n) = f(n-1) + f(n-2)表示。

而对于子问题的结果，则可以储存在一个一维数组里面。

自此，这道题就可以完美解决了。

三、买卖股票的最佳时机

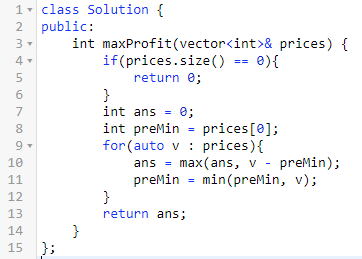
题意：给出一支股票连续若干天的价格。
假设我们只能买卖一次，怎么才能收益最大化呢？

思路：假设是n天，则问题可以拆分为两部分：第n天卖出，或者前n-1天操作。
定义f(n)为前n天买卖一次的最优解。
定义F(n)为第n天卖出一次的最优解。

则可以写出下面两个公式：

f(n) = max(f(n-1), F(n))
F(n) = A[n] - min(n-1)

min(n-1)为前n-1天股票的最低价。
由此，这道题我们就做出来了。

当然，拆分问题的时候，也可以拆分为：f(n) = max(F(n), F(n-1), ..., F(1))
不过此时，f(n)这个定义就没意义了，因为子问题里没有再出现这个定义。

四、最大子序和

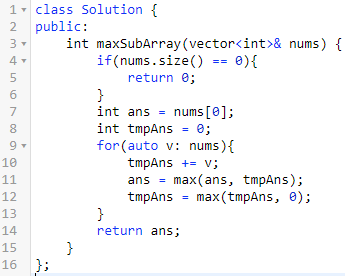
题意：给一个数组，找一个连续子数组，使得这个子数组的和最大，返回最大和。

思路：最经典的动态规划题。

按照上面一题的拆分思路，我们同样可以拆分为两个状态。
定义f(n)为前n个数字的最优值。
定义F(n)为第n个数字为连续数组最后一个数字时，最优值。

f(n)可以分两种情况，一种是最后一天属于连续数字，一种是不属于，结果去最优值。
即f(n) = max(f(n-1), F(n))

F(n)也可以分两种情况，一种是自己单独组成连续数字，一种是和前面的连在一起，结果也是取最大值。
即F(n) = max(A[n], A[n] + F(n-1))

看到这里，是不是发现这道题和上一题几乎一抹一样？
即f(n)可以拆分为假设每一天为连续数字的最后一个的子问题。
即f(n) = max(F(n), F(n-1), ..., F(1))

这里和上一题不同的地方在于，这道题我们知道一些必胜策略。
比如假设 F(n-1) < 0，那么F(n)的决策肯定是A[n]，而不是A[n]+F(n-1)。
因为A[n]肯定大于A[n]+F(n-1)的。

由于这道题比较简单，这个必胜决策的效果不容易看出来，但是大家需要知道有这么一个概念。
在搜索中，这种情况可以用于剪枝，用来过滤明显不是最优解的子问题。

五、打家劫舍

题意：给一个数组，我们可以挑选若干位置的值，使得和最大。
条件：挑选的位置不能连续。

思路：定义f(n)为答案。
则可以拆分为两个问题：第n个是否挑选。
挑选，则只能挑选前n-2个元素；
不挑选，则可以从n-1个元素开始挑选。
公式为f(n) = max(f(n-1), A[n] + f(n-2))

前面的几道题都是使用递推实现的，这个就使用递归实现吧。

六、最后

看了这四道题有没有发现动态规划还是很简单的呢？
如果给的题意就可以直接拆分子问题，则大部分都可以做出来。
如果题意不能拆分子问题，或者拆分的子问题无解，则需要转换一下题意，构造出一个可以拆分出子问题并求解的问题来。
当然，这里也是最难得。

随着大家的刻意练习，分析问题的能力会越来越强，那时候，大家就能够自己构造出可以求解的子问题了。

-EOF-