谷歌的一致性哈希算法

一、背景

三年前在《一致性hash基础知识》文章中，曾提到 google 有一个算法也是简单的计算就做到了一致性哈希需要做到的事情。

上个月在《一致性HASH技术的困境》文章的留言中，也有小伙伴提到，有一个 Jump consistent hash 算法可以做到一致性哈希的事情。

其实这两个说的是一个事情，那就是 google 有一个 Jump consistent hash 算法，可以通过数学运算做到一致性哈希效果一样好的平衡性。

那今天就来看看这个算法吧。

二、看代码

先看代码，下面就是全部的代码。

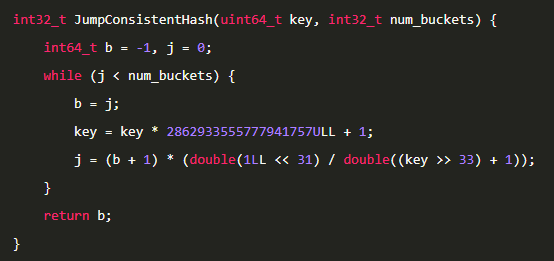
是不是感觉不可思议，这个代码的语法全部都懂，但是合在一起我们就看不懂了。
我第一眼看到这个代码的时候，也是一脸懵逼的。

这个算法是 Google 的 John Lamping 和 Eric Veach 创造的。
他们为这个算法写了一篇论文：《A Fast, Minimal Memory, Consistent Hash Algorithm》。

看了论文后，我才恍然大悟，原来是这样，果然是合理的。
如果你阅读原文论文，可以公众号后台回复“谷歌算法”获取论文。

三、算法原理

一致性哈希算法有两个目标：

1. 平衡性。即把数据平均的分布在所有节点中。
2. 单调性。即节点的数量变化时，只需要把一部分数据从旧节点移动到新节点，不需要做其他的移动。

我们根据这个单调性可以推算出一些性质来。
这里先另f(key, n)为一致性哈希算法，输出的为[0,n)之间的数字，代表数据在对应的节点上。

1. n=1 时，对于任意的key，输出应该都是0。
2. n=2 时，为了保持均匀，应该有1/2的结果保持为0，1/2的结果输出为1。
3. n=3 时，应该有1/3的结果保持为0，1/3的结果保持为1，1/3的结果保持为2。
4. 依次递推，节点数由n变为n+1时，f(key, n)里面应该有n/(n+1)的结果不变，有1/(n+1)的结果变为n。

这个使用概率公式来表示，就是这样的代码。

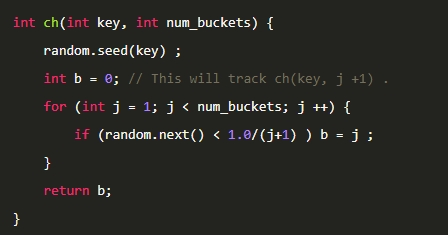
关于这个算法直接看可能还是看不懂。
所以需要使用实际数据模拟一下，见下图。

关键在于n=2到n=3的过程，每个数字的概率从1/2转化到了1/3。

之后，我们可以得出一个规律：增加一个节点，数据不发生变化的概率是n/(n+1) 再乘以之前每个数字的概率1/n，就可以得出每个数字最新的概率1/(n+1)

由此，可以轻松计算出n=4各数字的概率为1/4。 自此，我们可以确定这个算法确实是有效的。

这个算法唯一的缺点是复杂度太高，是O(n)的。
所以需要进行优化。

四、算法优化

在上一小节中，我们了解到f(key, n)算法的正确性。
除了复杂度是O(n)外，我们还可以确定，循环越往后，结果改变的概率会越来越低。

结果改变指的是，增加一个节点后，一个固定的key输出的结果发生了改变。
如果我们能够快速计算出这个固定的key在哪些节点下发生了改变，就可以快速计算出最终答案。

假设某一次结果是b，经过若干次概率测试，下一次改变为a，则从b+1到a-1这中间，不管节点如何变化，这个key的结果都是不会变化的。
根据上一小节的到的概率变化公式，新增一个节点数字不变化的概率是n/(n+1)。
那从b+1到i不变化的概率就是(b+1)/i（中间的抵消了）。

如果我们有一个均匀的随机函数r，可以确定当r<(b+1)/i时，f(i)=f(b+1)。
那么i的上界就是(b+1)/r向上取整。
这个上限也是下一次key发生变化的节点数量。

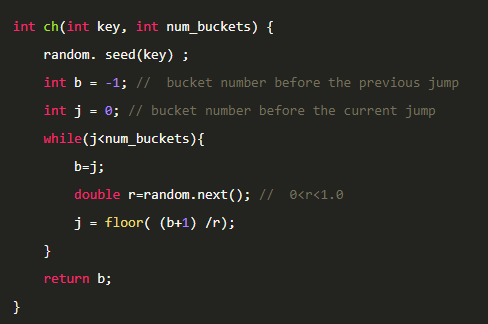
由于r是均匀的，所以期望是1/2。
这样，代码中j就是按照指数级增长的，平均复杂度就是O(log(n))了。

回头看看第一个代码，就可以看懂代码了。

第一个key=key*x+1算是一个伪随机生成器。
而j=(b+1)*x/y则是上面的求上界的公式，其中y/x通过浮点数运算来产生(0,1)内的一个随机数。
自此，这个代码就可以看懂了。

五、最后

谷歌能够创造这样一个算法确实了不起，但是从实际应用上来，这个算法也没有想象中的好。

如果你用过一致性哈希的话，会发现有很多问题。

因为我们实际使用时，节点往往是有权重的。
这里只有一个节点的最大值，那意味着，节点的扩散需要在外层实现。
也就是需要在外层来储存扩散后的节点列表。

既然外面储存了节点列表，按照 hash 值排序，就可以二分查找出符合要求的节点了。
如果使用 map 储存，也可以在 log 级别找到对应的节点。

由此，可以发现 谷歌的这个算法自身不需要内存了，但是内存需要业务自己维护，实际上还是需要的。

当然，如果你没使用过一致性哈希的话，你不知道我这个小节在说什么。
或者你可以看看之前我记录的一致性 HASH 文章，然后再回头看看这个小节。

-EOF-