Leetcode 第104场比赛回顾

一、背景

一个半月前，由于各种原因，暂停了比赛。
恰好昨天小组内进行了一次比赛联系，趁着这个机会重新开始写比赛记录。

这次是随机选择的一个比赛。
前三道题不需要高深的算法和数据结构就可以做出来，最后一道题大部分人就做不出来了。
因为最后一道题是博弈题，需要很强大的逻辑推理能力才行。

下面我们来看看这四道题吧。

二、卡牌分组

题意：给一副牌，每张牌上一个整数。
现在需要选出一个数字X，然后将这些牌分成若干组，每组恰好有X张牌，且每组内牌的数字相等。
要求：X至少为2。
问题：是否存在这样的X。

思路：首先需要统计每个数字出现的次数。
如果存在满足条件的X，则X肯定是所有数字出现次数的整数倍。

所以解决方法也就出来了，求所有数字出现次数的最大公约数，如果大于1就有答案了。

三、分割数组

题意：给一个数组，求一个位置，使得这个位置左边所有元素的最大值不大于右边所有元素的最小值。
问题：保证存在答案，输出这个位置的最小值。

思路：题意使用通俗的话讲，就是右边的元素都大于等于左边的元素。

最简单的方法就是枚举所有位置，并求出对应位置左边的最大值和右边的最小值。
复杂度O(n^2)。

面对这个复杂度肯定不能接受的，所以需要优化。
稍微一分析，可以发现每个位置左右的最值可以预处理得到。
于是，我们便可以先开两个数组预处理，然后在枚举每个位置计算出答案。
复杂度O(n)。

当然，实际上我们只需要计算出一个最值，另外一个在枚举位置的时候，便可以顺便求出来。

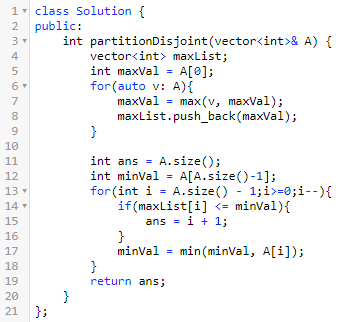
四、单词子集

题意：每两个单词数组A和B。

定义1：如果单词 b 中出现的每个字母都在单词a中（包括重复字母），则称单词b是单词a的子集。
例如：wrr是warrir的子集，而不是world的子集。

定义2：如果对于B中的任意一个单词b，b都是a的子集，则称a是通用的。

问题：求出A里面所有通用的单词。

思路：这道题有两个定义需要大家理解消化一下。
一个是子集的定义，一个是通用的定义。

不过还好，这个你应该读两遍就能理解了。
那该怎么做出这道题呢？

暴力计算的话，复杂度将会超过n^2，显然会超时的。

分析单词数组B，其实可以发现，对单词数组B的每个单词字母进行统计之后，统计数据是可以合并的。

例如B是"le","eoe"。
使用数学语言表示就是

le: 1个l，1个e  
eoe: 2个e，1个o  

如果一个单词a是通用的，则le和eoe都是a的子集。
所以B所有单词的统计都满足情况，所以可以对这些统计进行合并。

B: 1个1,1个e,2个e,1个o  

其中，如果满足2个e，那一定满足1个e。
所以，对于相同的字母统计，取最大值即可。

合并B之后，剩下的就一个个判断即可。

五、猫和老鼠

题意：给一个有向图。
老鼠起始位置在1，猫起始位置在2，洞的位置在0。
老鼠先走，猫后走。它们依次移动，每次只能移动一步，且只能移动到相邻的顶点上。

如果老鼠到达洞里，老鼠获胜。
如果猫抓到老鼠，猫获胜。
如果处于僵直状态，则算平局。

思路：起初看到这道题，很容易认为是图论题。
但是分析之后，发现这是一道博弈题，需要记忆化搜索来解决。

状态定义：f(whoMove, mousePos, catPos) 为whoMove要移动时，老鼠在mousePos，猫在catPos时最终的结局。
每个状态有三个结局：老鼠必死、老鼠必胜、未知。

在博弈里面，需要分别假设自己是两个角色，然后来进行逻辑推理。

假设当前状态需要猫移动，有多种状态选择。
只要有一种选择能够使老鼠必死，猫肯定会选择这个状态。此时当前状态是老鼠必死状态。
所有状态都是老鼠必胜时，猫就没有选择了。此时当前状态是老鼠必胜状态。
其他情况，说明至少有一种状态是未知的，猫如果不能杀死老鼠，那只能选择未知状态。

对于老鼠类似。
只要有一种选择能够使老鼠必胜，老鼠肯定会选择这个状态。
所有状态都是老鼠必死时，老鼠就没选择了。
其他情况，老鼠只能选择未知状态。

由此，我们就可以写出递归代码了。
这里贴一下老鼠博弈选择的代码，猫是类似的。

当然，想到这一步并不能AC这道题。
因为优先状态原先是未知，后面有可能变成必胜或者必败。
所以当新增一个必胜或必败状态时，需要重新展开计算周围的点。

我当时直接偷了一个懒，发现有必胜或必败，就重新计算全量数据。
由于有记忆化，实际上也不会超时。

当然，后面我维护了一个队列，把新增的状态保持下来，进行展开计算。
由于每个状态顶多入队一次，展开计算顶多遍历一遍所有顶点，所以复杂度是n^3。

六、最后

这次比赛的前三道题很适合用来当做面试题。
而最后一道题则只适合在比赛了，毕竟博弈题需要很强大的逻辑推理能力。

-EOF-

本文公众号：天空的代码世界aa 个人微信号：tiankonguse
公众号ID：tiankonguse-code