Leetcode 第 161 场比赛回顾

零、背景

上次的第 160 场比赛我没参加，昨晚的第 12 场单周赛我因为看 IG 比赛也没参加。

由于个人时间有限，没办法一一在公众号写成文章分享给大家了。

所以我想着可以利用零碎时间，在我的免费知识星球分享这些比赛题。

感兴趣的朋友可以下载知识星球 app 搜索“不止算法”加入星球，学习各种算法题解吧。

下面就来看看今天第 161 场比赛的题解吧。

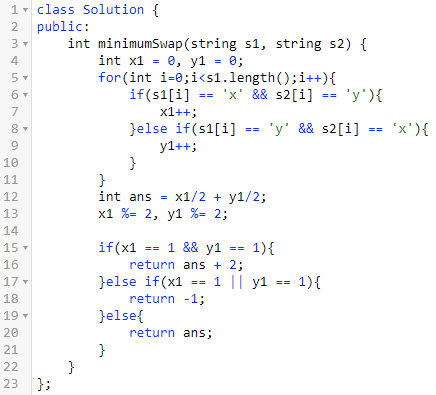
一、交换字符使字符串相等

题意：给两个长度相等的字符串，都只包含字母x和y。
问能够通过一系列交换，使得两个字符串相等。
如果可以，求最少交换次数。

交换规则：每次可以从两个字符串中分别挑选一个字符，进行交换。

思路：我们先来判断是否存在答案，然后再来寻找最优答案。

假设第一个字符串在上面，第二个字符串在下面。
则相同位置的字符存在四种组合。

1）上下都是x，不需要交换。
2）上下都是y，不需要交换。
3）上是x，下是y，记为x出现的次数。
4）上是y，下是x，记为y出现的次数。

可以发现，对于情况一和情况二是不需要交换的，我们只需要对情况三和情况四进行交换。

而对于两个情况三，我们通过一次交换则可以使两个位置都相等。
例如对于 xx 和 yy 字符串，一次交换后，就都可以变成 xy 了。

情况四也一样，可以一次交换消除两个不相等的位置。

那先进行两两交换，最后依旧剩余四种情况。

P1）零个情况三、零个情况四
P2）零个情况三、一个情况四
P3）一个情况三、零个情况四
P4）一个情况三、一个情况四

面对这四种情况，可以发现P1已经使两个字符串相等了。
而P2和P3由于字符的个数的问题，无论如何也没办法使两个字符串相等。
对于P4，则还是可以相等的，只是没办法一次交换消除两个了，需要两步才能使字符串相等。

具体操作步骤是：先上下交换，然后交叉交换，如下图。

yx => xx => xy
xy => yy => xy

由此我们就可以判断是否有答案了。

那怎么证明上面的步骤是最优的呢？
其实很简单，一次交换最多可以消除两个，如果都能消除那就是最优答案。
如果没有消除完，那最后肯定是P4状态，需要多一次操作才能消除。

而其他交换，则是一次消除一个或者都不消除，这样自然需要更多次数了。
想想每次减二与每次减一或不减，谁更快到达零呢？

二、优美子数组的个数

题意：给一个数组，如果某个子数组里面奇数的个数恰好为k个，则称这个子数组为优美子数组。
求优美子数组的个数。

思路：

第一种方法是暴力枚举所有的子数组，判断是不是优美子数组。
子数组个数是N^2个，判断需要N次，所以复杂度是N^3，肯定超时了。

第二种方法是以某位置开始，枚举判断这个位置为前缀的优美子数组个数。

由于是前缀，可以累积统计奇数的个数，所以判断复杂度就是O(1)了。
但是子数组这个是硬伤，总体复杂度是O(n^2)，ACM中还是超时，LeetCode 上我没试。

第三个方法就是滑动窗口了。
我们先看一个最优子数组，如果这个子数组右边相邻的数字还是偶数，则把这个偶数加进来依旧是优美子数组。
左边也是一个道理。

大概如下图。

0001...10000

假设两个1这个子数组已经使最优子数组了。
左边有3个偶数，右边有4个偶数，左边和右边任意选择形成的子数组都是优美的。

左边可以有4中选择（选0~3个），右边可以有5中选择（选0~4个）。
由于左边和右边互不影响，所以共有4*5=20中选择。

所以我们每找到一个左右边界都是奇数的最优子数组时，统计左右偶数的个数，就可以求出总个数了。

由于只扫描一遍数组，复杂度是O(n)。

三、移除无效的括号

题意：给一个字符串，其中有一些左括号和右括号。
求删除最少的字符，使得括号匹配，但会删除后剩余的字符串。

思路：肯定只删除括号字符了。

这里其实有一个知识点都被大家忽略了，从而导致第一次看这道题，不知道怎么做。

我们怎么判断一个字符串是否是括号匹配的？
使用栈尽量的去匹配，直到遍历完了栈中还有左括号，或者遇到右括号但是栈为空。

对于第一种遍历完了，这个其实就已经找到了最长的能够匹配的括号了。
栈中的都是左括号，只能删除。

而对于第二种遇到右括号栈为空，那当前字符确实没啥用，删除就行了。

所以这道题就变得简单了，在遇到第二种情况时，标记删除，然后继续匹配即可。

四、是否是好数组

题意： 给一个正整数组成的数组，问是否可以从数组中挑一些元素，使得这些元素乘以任意一个整数，使得和为1。

例如，对于12,5,7,23数组，我们挑5和7，然后就可以5*3 + 7*(-2) 得到1了。

思路：其实这道题比较迷惑人。
我们完全可以使用这个数组来当做几个，对于那些没挑的元素，使用整数0就行了。

所以接下来问题就是，怎么判断这个数组有没有答案。

先来看两个数字，什么时候才可以组合得到1呢？
显然是最大公约数为1的时候，其他时候肯定都有答案（高中数学知识）。

证明也很简单。
假设我们是用过递归减法来证明最大公约数是1，这个递归减法的展开就是两个数字的加加减减。
使用递归取模来证明也一样，取模本质上是进行了很多次减法嘛。

如果是多个数字呢？那自然判断多个数字的最大公约数是否是1了。
证明其实和两个数字一样。

第一步先两个数字加加减减得到最大公约数，如果是1结束。
第二步，如果还有下一个数字，使用前面得到的最大公约数当做新的数字，回到第一步，来与下一个数字求最大公约数。
第三步，此时最大公约数不为1，没有答案。

五、最后

这次比赛其实还算简单，做题耗时如下。

第一题用了19分钟。 第二题用了20分钟。 第三题用了8分钟。 第四题用了4分钟。

不过由于我的敲代码速度比较慢，这次比赛排名还是比较靠后。

后面我继续启动练习打字了。

以前，我习惯于读电子书。
对于那种几十分钟的电子书音频讲解，我之前是抗拒的。

因为我觉得那种效果不大。
就像现在的很多课程，XXX技术的五大问题，XXX技能20讲，XXX技术三十六招等等。

看着很有用，但是实际学习的时候，发现很像鸡汤。
那些课程一会就听完了，没有自己的实践，没有自己的思考，没有自己的沉淀，最后自己心中只知道一些名词，其他的什么都没留下。

为什么会这样呢？上面我提到了，没有实践、思考、沉淀。
如果我们能够自律的进行实践练习、反复琢磨思考为什么，最终形成自己的方法论后，那这些课程自然是有用的。

另一方面，如果看一本书前能够提前大概了解一下对应的核心主题，那对读书也有很有帮助的。

所以，昨天我尝试下载了樊登读书 app，阅读了推荐给我的几本书，比如《终身成长》、《刻意练习》、《非暴力沟通》等。
发现还是学到不少东西。

比如《终身成长》里面，人在某一领域的成功与失败关键在于思维模式的差异。
失败的人是固定型思维，成功的人是成长型思维。

固定型思维的人遇到糟心事会认为运气不好，失败了会怪别人，或者认为自己就这样不会成功的。
成长型思维的人遇到糟心事会有逻辑的分析原因，探究根本，寻找解决方案。

比如 LOL 比赛，固定型思维就是比赛失败了，认为自己就这样了，年纪大了，个人能力有限。
而成长性思维遇到比赛失败时，会想为什么失败，对方为何能成功，能不能从对面学习等等。

这其实也对应一句名言：失败是成功之妈。
但是前提是你需要有成长型思维。

书中还介绍了很多例子来来介绍之间的差异，以及我们应该如何培养，感兴趣的可以扫描下面二维码免费阅读。

-EOF-

本文公众号：天空的代码世界
个人微信号：tiankonguse
公众号ID：tiankonguse-code