Leetcode 第 165 场比赛回顾

零、背景

前几周比较忙，未来一个月也比较忙。
忙到晚上不想写文章了，只想静静的坐在那里。
于是追了一部电视剧，名字叫做《庆余年》。

看后发现这么电视剧的剧情和之前写过的一篇文章《将夜》很类似，未来的剧情也可以猜测的八九不离十了。
如果你喜欢看修仙玄幻剧，或者闲着无聊，可以去看看，腾讯视频有这么剧。

扯远了，接下来看看今日的比赛吧。

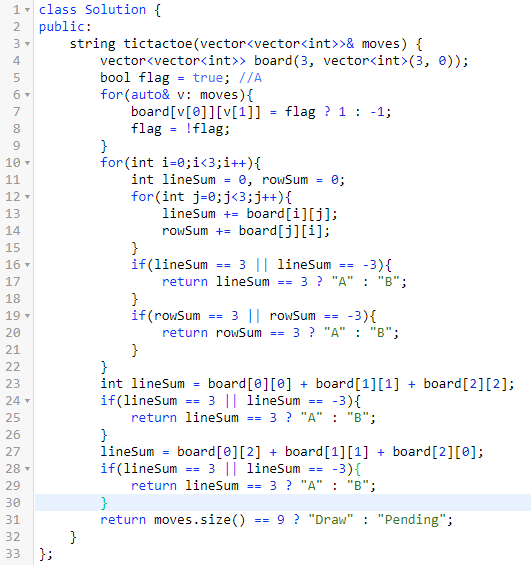
一、三子棋获胜者

题意：给一个三子棋棋谱，问目前棋谱处于什么状态。
三子棋的含义是相同颜色的棋子三子成线时，这个颜色就算胜利。
如果棋盘满了，依旧没有胜出者，则成为和局。
如果棋盘没满，也没有胜出者，则成为进行中的棋局。

思路：先根据输入构造棋盘，然后判断是否有胜出者。
没有胜出者时判断棋盘是否满了即可。

##二、汉堡分配

题意：有两种汉堡。
巨无霸汉堡由 4 片番茄和 1 片奶酪组成，小皇堡由 2 片番茄和 1 片奶酪组成。
现在给一些番茄和奶酪原材料，制造两种汉堡的时候，问能否恰好把原材料都用完。

思路：其实这个是一道初中数学题。

令番茄有 a 个，奶酪有 b 个。
假设最终制作了 x 个巨无霸，b 个小皇堡。
则可以得到两个等式关系。

4x + 2y = a  
x + y = b  

解方程得

x = (a-2b)/2  
y = (4b - a)/2  

当 x 和 y 都大于等于 0 时，就代表合法，否则就是不合法。

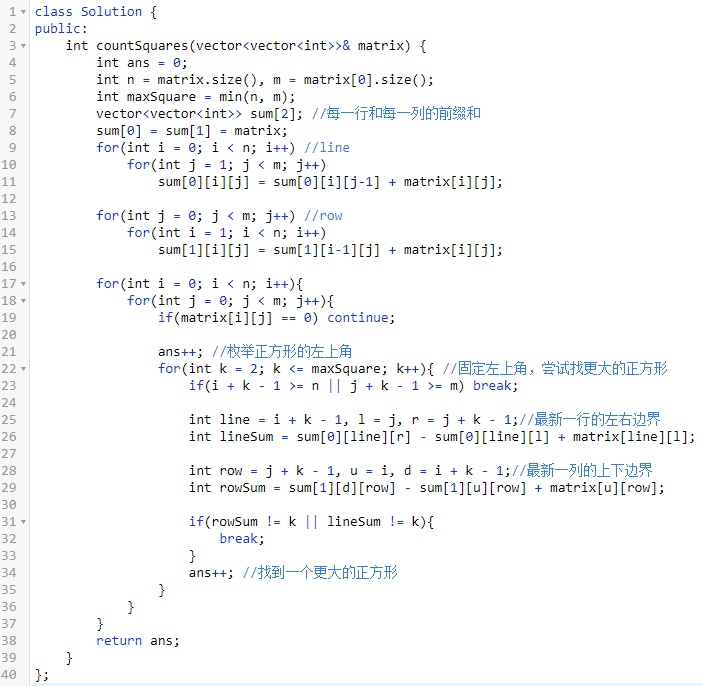
三、全为1的正方形个数

题意：给一个0/1 矩阵，问全为 1 的正方形的个数。

思路：最简单的方法就是暴力枚举所有正方形，然后判断是否满足要求。

哪有多少个正方形呢？
先枚举左上角，有 n^2 个，再枚举边长，综合有 n^3 个正方形。
枚举出了正方形，还需要判断是否满足要求，这样复杂度又是 n^2 。
这样错略一估计，复杂度是 n^5 的了。

但是不要慌，判断正方形这里我们是可以使用前缀和优化的。

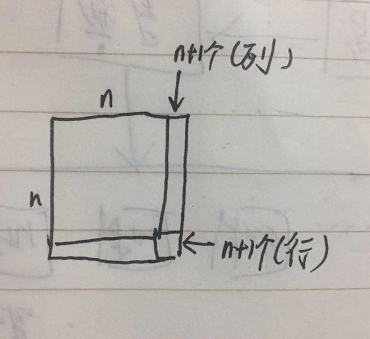
大概如上图，假设我们已经确定当前左上角存在一个n*n的正方形，判断是否存在n+1为边的正方形时，只需要判断新增加的行和列即可。
如果新增加的行和列全为1的话，行和列的区间和应该都是 n+1。

求区间和的技巧之前教过大家，预处理出前缀和，则可以O(1)的时间内求出区间和。
这样，我们就可以在O(1)的时间内判断正方形是否合法了。

综合复杂度：O(n^3)

那这个能不能继续优化呢？
还真可以。

还是枚举左上角，至于正方形的边长，二分来求满足条件的最大值。
假设找到的是k，则边长1~k都是满足条件的正方形。
综合复杂度：O(n^2 log(n))

四、分割为k个回文子串

题意：给一个字符串，问最少修改多少个字符，才能将这个字符串分割为 k 个回文子串。

思路：第一眼看到求最小值时，马上想到了二分。
但是又一想，直接递归枚举搜索也可以求出最优值，这样动态规划就可以做这道题了。

定义：f(k, b, e) 代表将字符串 [b, e] 分割为 k 个子串的最小修改次数。
状态转移方程：依次枚举第一个子串的长度，剩余的递归处理，挑出最优值。

f(k, b, e) = min(firstString(b, i) + f(k-1, i+1, e))  

而对于一个固定字符串，将其变为回文串的修改次数也可以快速求出来。

综合复杂度：O(n^3)

五、最后

这次比赛的题不错，一个是矩阵题，一个是字符串题。
不说了，最新没啥想法，脑子一片空白。

-EOF-

本文公众号：天空的代码世界
个人微信号：tiankonguse
公众号ID：tiankonguse-code