Leetcode 第 171 场比赛回顾

零、背景

这次比赛的题不难，可是我状态不好，各种看错题，头脑不清晰，导致做了好久才做完这四道题。

原先我还计划录制了视频，题没做好，视频也没录好，这算是当场翻车了。

不过我厚着脸皮上传到了B站。
想看视频的同学可以在公众号里回复B171获取比赛视频。

一、数字拆分（二）

题意：给一个数字n，问是否可以拆分为来两个数字，这两个数字之和是，且数字中没有0。

思路：数据范围只有一万，暴力枚举即可。

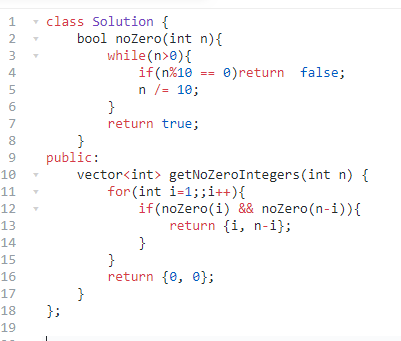
那能不能直接使用O(1)的方法构造呢？

我们直接从低位到高位把对应的数字拆分为两个不为0数字之和。
只有为0和1时不能拆分，此时去高位借位即可。

对于最高位，如果是1的话，只拆分给一个数字。

二、或操作最小修改数

题意：给两个数字，问最小修改多少次，能够是两个数字的或运算等于目标数。

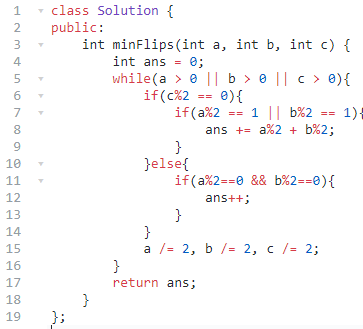
思路：由于每一位完全独立，那对每一位特殊判断即可。

如果或之后，与目标位数相同，则不需要修改。
如果不同，则需要修改，分两种情况。

目标位数是1，那说明两个数字的位数都是0，随便修改一个即可。
目标位数是0，那说明两个数字的位数至少有一个1，全部修改为0才行。

三、最小修改使得网络连通

题意：给一个网络，问能不能修改一些边，使得网络连通。
修改边的意思是，我们可以删除一条边，再加入任意一条边。
求最小修改次数，如果没答案输出-1。

思路：可以看出来，修改不会变更边的个数。
而一个联通图最少需要n-1条边，所以边数小于n-1时肯定没答案了。

而边数足够时，则需要统计联通分支的个数。
联通分支就是一个完整的联通图，不同的联调分支之间没有边。

由于肯定有答案，我们可以删除一个冗余的边，然后将两个联通分支连接起来。
这样，每操作一次，联通分支的个数就会减一。
当联通分支的个数为一时，就代表整个网络都是联通的了。

所以最小修改次数就是联通的个数减一。

怎么求联调分支的个数呢，一个DFS或BFS或者并查集都可以。

四、两指的最小移动距离

题意：给一个定制化的纯字母键盘，我们只使用两个指头敲字。
给一个字符串，问两个指头总共需要移动多少距离。
特殊条件：每个指头第一次敲字时，按不需要移动处理。

思路：我的第一感觉是优先队列+剪枝搜索。

大概思路就是每个字母分别假设两个指头来按，然后计算对应的代价。
最终取最低的代价。

全部做完之后，我突然意识到，优先队列其实没啥用。

因为进行BFS搜索的时候，队列的pos就是递增的。

只是可能相同的pos，有不同的step而已。 但是这些step最终都要处理的。
但是调了很久，发现队列就超时，优先队列就不超时。

后来，我在写这篇文章的时候还是相同了。
优先队列使更小的step优先处理，那更小的答案就会缓存起来，这样那些明显不是最优答案的步骤就可以被剪枝掉。

也就是说，只看优先队列的话，没有区别。
但是和剪枝结合起来，就可以大大降低队列的大小了。

在我想不明白队列与优先队列的关系时，本来想着结束录制视频，去吃饭了。
在那一刹那，突然发现这道题其实就是一个非常简单的动态规划题。
两层循环就搞定了。

于是我继续写动态规划的方法。

状态定义：dp[i][j]一个手指在第i个字母，一个手指在第j个字母时的代价。
由于两个手指之间没有关系，所以存在对称性，这里假设i<j。
只有起始条件两个手指在相同位置，之后不可能在相同位置。

为了减少不必要的状态，我们定义，每次状态转移时，两个手指必须交叉前进才行。
具体意思是， 假设当前状态是dp[i][j]，那下一个状态肯定是d[j][k], k>j。

这样的物理意义就是，首先把i位置上的手指先从i位置移动到j+1位置，然后从j+1位置一直按到k位置。
而从j+1到k由于是连续按的，我们就可以使用前缀和来快速计算。

这样总体状态转移公式就是dp[i][j] = dp[k][i] + cost(k, j)

这个思路没错，但是会发现复杂度是O(n^3)的，直接超时了。

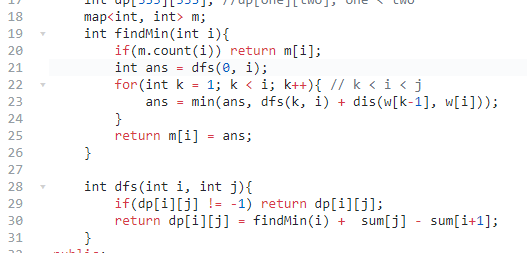
然后分析dfs函数，会发现函数内的k循环满足单调性。

具体来说，可以发现所有的k都会加上sum[j] - sum[i+1]，那删除这个公式后，k循环竟然与j没关系了。
也就是说，对于每个(k,i)，我们计算了n次，可以提前计算好缓存起来。

所以就可以将单调性提取为一个函数，将计算过的数据缓存起来，复杂度就降为O(n^2)了。

五、最后

这次比赛最优一题代码量有点大，但是难度其实还好，尤其是搜索的方式，之前遇到很多次了。
然而我并没有做好比赛，算是翻车了。

录得视频已经上传到了B站。
想看视频的同学可以在公众号里回复B171获取比赛视频。
想获取比赛源码的同学，可以在公众要回复L171自动获取。

-EOF-

本文公众号：天空的代码世界
个人微信号：tiankonguse
公众号ID：tiankonguse-code