我尝试做了做阿里巴巴全球数学竞赛题

零、背景

上周六的时候，朋友圈看到有人分享《阿里巴巴全球数学竞赛题》，我便花了半个小时尝试做了一下，发现也不难。

今天把大概思路分享给大家。

一、拓扑环

大概题意是给一个圆环，剪开转几圈再连接为环。
之后从圆环中间剪开，问会怎么样？

完整题意如下：

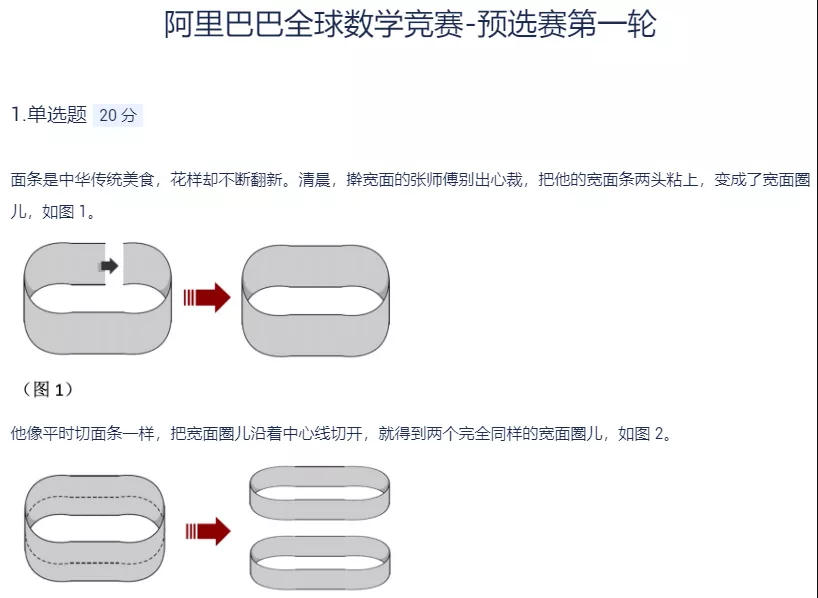
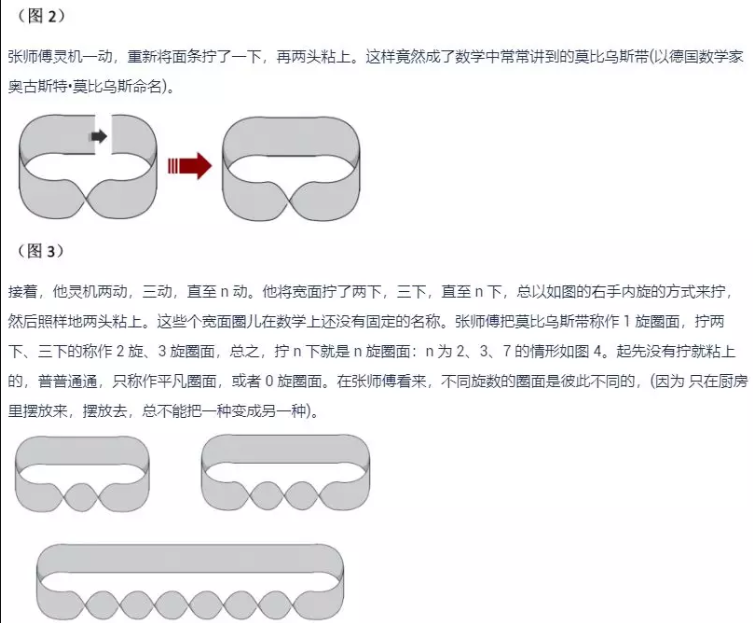
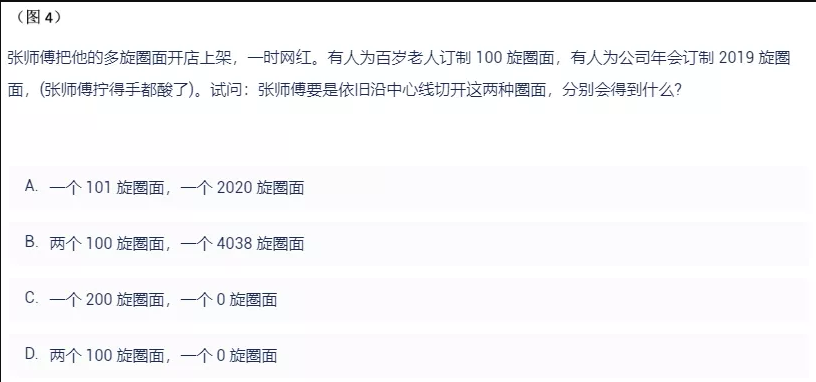
面对这个题，其实很简单。

原问题是一个转100圈，一个转2019圈，问会得到什么。
实际上我们可以抽象为一个是转了偶数圈，一个转了奇数圈。

此时我们只需要求出偶数圈会怎样，奇数圈会怎样。

对于偶数圈，0 就是偶数。
不转的时候剪开就是两个环。

因此我们可以得到两个 100 旋圈面。

而对于奇数，剩余的一个答案是 0 旋，一个是 4038 旋。

所以可以猜想有两种可能。
一种是连续奇数是一次是抵消为0，一次 double。
另一种可能是奇数的答案是固定的。

我分别模拟了旋1次与旋3次的场景，发现都没有抵消。
所有对于奇数，可以确定是翻倍的了。

所以答案选择 B。

二、线性代数

第二题是一个线性代数题，不过看到只有矩阵每个位置只有两个值，我笑了。

这个也可以成为计算机题了，再熟悉不过了。

题意有两个假设。
假设一：任意两行进行 * 运算，得到的结果属于某一行。
假设二：任意两行进行 . 运算，结果为0.

证明一直接套假设二就可以得到结论。

证明二是集合论或者群伦的知识。
每个位置有 2 个可选值，要做到假设一这种闭环，必须有 2^m 个状态。
这个可以使用反证法来证明。

证明三是证明二的推论。

三、解方程

一看是一元三次方程，先去网上搜一个解的万能公式。

第一小题带入万能公式，就可以解除一个多项式解来。

第二小题要求有三个不相等的解，需要根据万能公式解之间的关系来求，对数学感兴趣的同学可以去求一下.

四、概率题

第一小题就是一个N皇后题，由于数据较小，手动计算也可以找到所有答案。

第二小题则是常见的概率题。

第一小格胡杨概率是 r。
第二小格胡杨概率是 rs + (1-r)(1-t)。

由于概率不变，令 r == rs + (1-r)(1-t)。
解得 s/2 + 0.5 = t。
所以存在答案。

第二小题的第二个问题，也可以计算出来。
首先计算出下一个胡杨的概率是：r * 11/20 + 1/5。

我们可以计算出第 2019 格子是胡杨的概率。
现在告诉我们 2019 的概率了，那这就是典型的条件概率了，套公式即可。

第三小题题目太长，看着公式那么复杂，还有极限什么的，我便知难而退不看了，你们谁会可以留言告诉我。

五、最后

这样看来，这次四道题还不算太难，你认为呢？

《完》

-EOF-

本文公众号：天空的代码世界
个人微信号：tiankonguse
公众号ID：tiankonguse-code