leetcode 第193算法比赛

零、背景

这次参加 Leetcode 比赛，看着题都不难，代码敲出来后，分析复杂度也没问题，就是过不了。
最后做了很多无意义的优化，最后才全部通过。

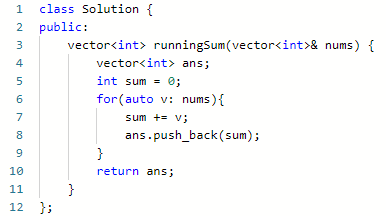
一、一维数组的动态和

题意：求出数组所有位置的前缀和。

思路：循环累加即可。

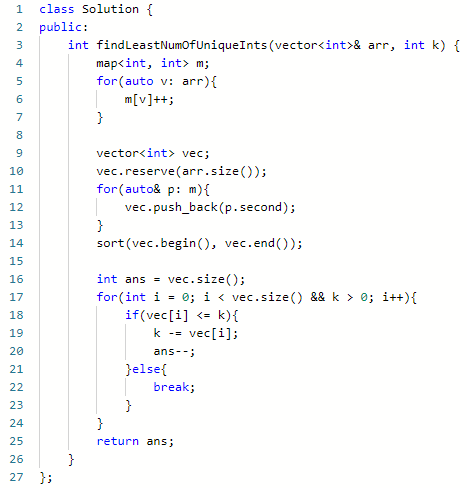
二、不同整数的最少数目

题意：给一个数组，删除 k 个数后，剩余的数字去重后有 X 个。
问怎么删除才能使 X 最小，输出最小的 X。

思路：典型的统计题。

1、使用 map 进行分组统计
2、根据个数从小到大排序
3、从前到后删除即可。

三、制作 m 束花所需的最少天数

题意：给一个数组，值 v 代表对应位置的花在第 v 天开放。
每朵花只能采一次，数组中连续的 k 朵花可以组成一束花。
问需要等多少天才能采到 m 束花。

思路：枚举天数，判断这一天是否可以采 m 束花。

由于天数在 10^9，我们可以只枚举实际有效的天数，即有花开的那些天数。

如果不做预处理，复杂度是 O(n^2) 的复杂度，显然会超时。

所以需要预处理，保存一个前缀，即已经开花的数据。
后面有新的花加进来时，动态更新即可。

由于是找长度为 k 的连续区间，我们可以预处理保存所有区间，以及满足连续区间 k 的个数。
这样每次加入新的花朵后，只需要判断个数是否大于 m 即可。

关于怎么储存区间，之前在《leetcode上的几个区间题》文章分享过。

具体来说就是，使用 map<left, right> 来表示一个区间。

unordered_map<int, int> allRange;   // pos -> right
long long m, k, num;
void delRange(int nextLeft){
    if(allRange.count(nextLeft) == 0) return;
    num -= (allRange[nextLeft] - nextLeft + 1) / k;
    allRange.erase(nextLeft);
}
void addRange(int nextLeft, int nextRight){ 
    allRange[nextLeft] = nextRight;
    num += (nextRight - nextLeft + 1) / k;
}

每次加入一个新的花朵，区间操作有四种情况。

1、形成新的独立区间
2、加入前区间，[o o] o
3、加入后区间，o [o o]
4、把前后区间连起来，[o o] o [o o]

对于前区间（情况1和情况4），这里有一个问题：需要根据区间的右边界找到区间的左边界。
所以我们还需要加一层，维护一个 区间内元素到左边界的映射。

加了一层就带来了新的问题。
合并后区间的时候，后区间所有元素的左边界都会更新，这样更新复杂度就退化为O(n)了。
所以我们使用延迟更新技术来优化，即并查集算法。

unordered_map<int, int> posToRange; // pos -> left
int getLeft(int pos){ //并查集
    if(posToRange[pos] == pos)  return pos;
    return posToRange[pos] = getLeft(posToRange[pos]);
}

说来惭愧，我公众号没讲解过并查集。
所以大家可以自行去翻一下大学的数据结构与算法教材，这个算是最经典的算法之一。

通过map储存所有区间，通过并查集来辅助更新区间，我们就可以快速计算出答案了。

排序复杂度：O(n log(n)) 区间计算复杂度：O(n log(n))

这道题我被卡超时了。
因为我在进行排序的时候，没有使用 vector+sort，直接使用的 map<int,set<int>>。
后来改成vector+sort后依旧被卡超时。

最后把map换成unordered_map，然后就过了。

四、树节点的第 K 个祖先

题意：给一个有根树，0 是根，输入是每个节点的父节点。
问某个节点第 k 个祖先节点是什么，如果不存在输出 -1。

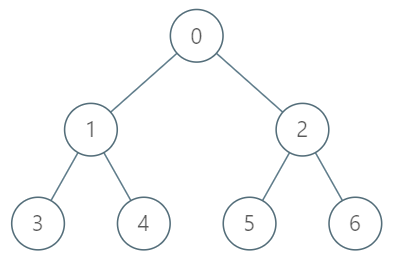
如上图，3 的第一个祖先节点是 1，第二个祖先节点是 0，第三个祖先节点不存在。

思路：暴力方法是循环求第 k 个祖先节点。

查询次数 n 和 k 都是 5*10^4，那复杂度最坏情况是 O(n*k)，必然超时。
我试了下，确实超时了。

面对 n=5*10^4 的数据，查询的次数已经是O(n)了，计算复杂度只能是 O(1) 或者 O(log(k))了。

O(1)意味着所有答案全部计算出来，这本身就是O(nk)的复杂度，不可行。

所以只能寻找O(log(k))的复杂度算法了。

log(k) 是树上的复杂度，于是我想到多建几条索引来加速查找。
索引之间有指数间的关系，这样就可以建立log(k)条索引，完美解决。

什么意思呢？
假设节点 n 有 10 层，我们就建1+log(10)条索引，即 4 条索引。
即把第1个祖先节点，第2个祖先节点，第4个祖先节点，第8个祖先节点都计算出来。

这样查询f(n, 10)的时候，可以等价于f(f(n,8), 2)。
即先找到第 8 个祖先节点，然后再向上找到第 2 个祖先节点。

大概思想明确了，剩下的就是代码实现了。

PS：这里又被卡超时了，map 换成unordered_map就过了。

五、最后

这里比赛后三题都不错，很有意思的题。
只是时间上卡map就没意思了，重点应该放在卡算法与复杂度上。

比如第三题，复杂度是2 * n log(n) 就超时，改成 n log(n) + n 就过了，没意思。
比如最后一次，map的大小只有log(k)个，复杂度操作就是log(log(k))，使用map超时，unordered_map不超时，卡一个log(log(k))的复杂度，也没意思了。

思考题：这次比赛你有不一样的解题思路吗？

《完》

-EOF-

本文公众号：天空的代码世界
个人微信号：tiankonguse
公众号ID：tiankonguse-code