leetcode 第194算法比赛

零、背景

这次比赛的题有点意思。

而且比赛的时候，我又犯了一个犯了无数次的错误。

比赛的时候，目标是快速通过题，不是寻找最优解。
第二题就被坑了，5 * 10^4的数据范围，ACM 使用 n^2 的复杂度肯定超时，leetcode 赛制不会超时。
我想到一个 n log(n)的方法，写了半个小时。
后来花了几分钟写了n^2的暴力代码，一下就过了。

看榜单不少人被这道题坑了，直接使用暴力方法，这次比赛能进前 50 名。

下面来看看四道题吧。

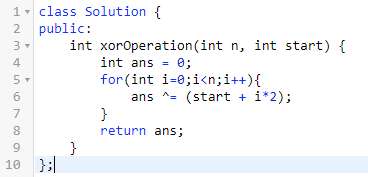
一、数组异或操作

题意：给 n 个数字，每个数字的值是 start + 2*i。
求所有数字的异或值。
数据范围：1000

思路：

由于数据范围比较小，第一个方法是直接暴力即可。
复杂度：O(n)

第二个方式是数位DB，即 DFA 算法。

不过在使用这个算法之前，需要先对数据稍微进行转换。

定义下面三个公式

1、f(i, a) = a + 2 * i
2、F(i, b) = b + i
3、ans(n, a) = ans(n-1) ^ f(n, a) 4、Ans(n, b) = Ans(n-1) ^ F(n, b)

对于 ans(i)的二进制个位，答案是固定的。
如果 start 的二进制个位是 1 且 n 有奇数个时，答案的个位才能是 1。

此时答案转化为ans(n, a)= Ans(n, a/2) << 1 | (start & 1 & n)

这样，一个间隔连续区间数字的异或，就转化为了连续区间数字的异或。

而对于区间问题，可以转化为前缀问题，即定义下面函数。

P(n) = P(n-1) ^ n
Ans(n, b) = P(n+b) ^ P(b-1)

而对于一个连续数字的取模问题，答案是固定的，所以我们可以通过 DFA 来计算。

假设 n 的可以表示为2^k + j。
则P(n)可以分为下面三部分的异或。

1、非高位数字 P(2^k)
2、高位数字的地位 P(j)
3、高位数字的最高位 j-1 个 2^k，判断奇偶性

则P(n) = P(2^k) ^ P(j) ^ ((j&1)<<k)

对于P(2^k)的答案固定为2^k，k=1除外。 P(2^k)与(j&1)<<k结合，可以确定j的奇偶性决定了高位是否有1。

因此我们能在log(n)的复杂度内计算出答案来。

第三个方法是在方法二的基础上进一步研究，即找规律。
复杂度：O(1)

对于 P(n) = P(2^k) ^ P(j) ^ ((j&1)<<k) 我们全部展开，会发现答案由最后两位决定。

后两位分四种情况。

1、n%4=00, P(n) = n
2、n%4=01，P(n) = 1
3、n%4=10，P(n) = n+1
4、n%4=11, P(n) = 0

上面的四种情况使用归纳法即可证明。

二、保证文件名唯一

题意：有 n 个文件名，现在要创建对应的文件。
如果创建文件的时候文件已存在，则需要加上(k)后缀名，其中k是最小的正整数。
输出：实际创建的文件名列表。

思路：

方法一：按照题意暴力模拟即可，复杂度O(n^2)。

方法二、预处理。
复杂度：O(n log(n))

可以发现，我们暴力的逻辑是来查找最小的正数的。
那如果预处理好数据，建好索引，就可以O(log(n)) 找到最小正数。

假设我们已经有每个前缀对应的整数了，即如下的索引。

preName => 0
preName => 1
preName => 2
preName => 5
preName => 7

现在再次写入 preName 的时候，我们的目标是快速计算出最小的正整数 3。

假设我们有一个带计数的 map, 我们就可以通过二分查找来快速计算出最小未出现的整数了。

例如我们把索引转化为这样的数据

preName => 0
preName => 1,1
preName => 2,2
preName => 5,3
preName => 7,4

首先搜素区间是[1, 5)，计算出中间值3。
在计数上二分查找，可以快速找到 5,3 这个数据。
判断发现索引 5 是第三个，说明 5 前面只有两个数据，最优答案在前面。

此时搜素区间是[1,3) 计算出中间值 2，此时发现最优答案在 2 后面。
所以搜素区间变成[3,3)，找到答案。

关于计数上的二分查找，可以使用线段树来实现。
这样这道题就使用 n log(n)完美解决了。

三、避免洪水泛滥

题意：有很多湖泊，第 i 天可能会下雨把第 rains[i] 个湖泊装满水。
如果第 i 天没下雨，即使旱天，我们可以随机选一个湖泊把水倒掉。

要求：如果一个湖泊下雨的时候已经装满水了，则会发生洪水。
问我们是否有策略防止发生洪水，如果可以，输出其中一个答案。

思路：二分查找题。
复杂度：O(n log(n))

如果某一天没下雨，使用一个数据结构记录下这个天数。
如果某一天下雨了，湖泊没水，装满水即可。
如果某一天下雨的时候，湖泊是满的，我们就需要在之前找一个旱天，能否把这个湖泊的水倒掉。

注意事项：找的旱天必须是在这个湖泊下雨之后的，下雨之前的不行。

所以这里需要找到大于上次下雨之后的第一个旱天，使用lower_bound即可。

四、最小生成树的关键边和伪关键边

思路：给一个无向图，求最小生成树的关键边和伪关键边。
关键边定义：去掉树上的这个边，图中就不能得到之前的最小生成树。
伪关键边：去掉树上的这个边，图中还可以构造出最小生成树。

思路：次小生成树算法。

步骤：

1、随便构造一个最小生成树。
2、剩余的边一次尝试加入最小生成树。
3、加上当前加入的是边 v，形成的环上看是否存在与当前边相等权重的边。
4、如果存在，则当前边是伪边，那些相等的边也都是伪边。
5、树上未被证伪的边则是关键边。

可以发现，对于关键边没发一个一个计算，只能找到一个集合，然后来证伪。

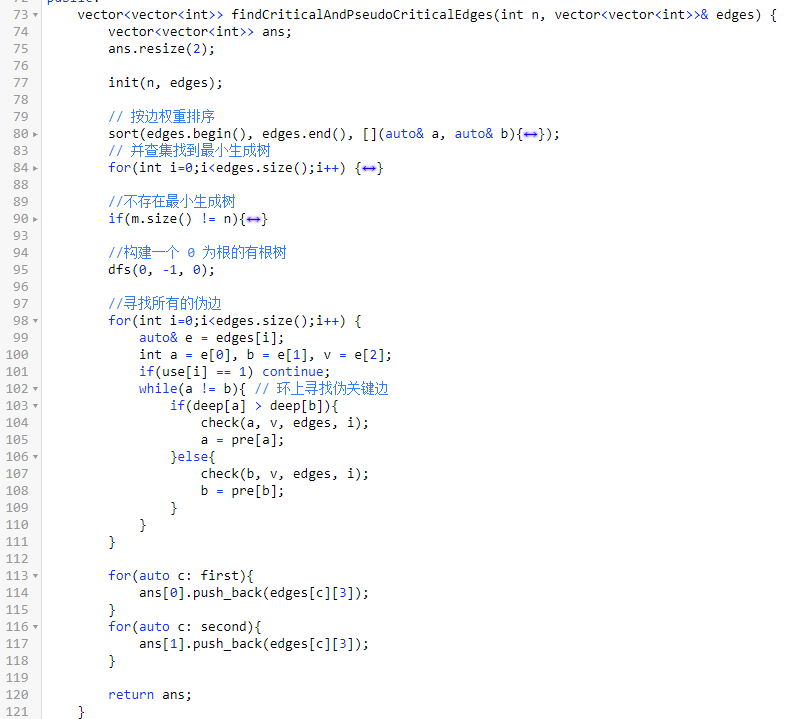
PS1：四五年没写最小生成树了。
我使用并查集来找到书，然后使用 dfs 转化为有根树。
如果使用 prime 算法的话，直接就是有根树了吧。

五、最后

这次比赛的题整个看来还不错，如果第二题没浪费半个小时的话，四道题应该都可以过。
但是没有如果，最终只过了三道题。

遇到树的题，我也就会最小生成树了，再难我也不会了。

思考题：对于这四道题还有其他解法吗？

《完》

-EOF-

本文公众号：天空的代码世界
个人微信号：tiankonguse
公众号ID：tiankonguse-code