leetcode 第 231 场算法比赛
作者: | 更新日期:
这次难度有点大。
本文首发于公众号:天空的代码世界,微信号:tiankonguse
零、背景
这次比赛难度有点大。
前两道题几分钟就通过了。
第三题好久没做图论题了,手生了,最后敲出来了又忘记取模了。
第四题想到枚举DP,但是看错数据范围了,认为枚举内存会爆掉。
果然面试题都变得这么难了。
如果你没有做比赛,第四题不需要看了,文字比较抽象,你可能看不懂。
一、5697. 检查二进制字符串字段
题意:给一个 01 二进制,问是否只有一个连续 1。
思路:这道题有点小坑,一个 1 也算连续 1 的。
所以起始值假设为 0,然后只需要判断 0 到 1 转化的次数即可。
bool checkOnesSegment(string s) {
int num = 0;
char pre = '0';
for(auto c: s){
if(c != pre){
if(c == '1'){
num++;
}
pre = c;
}
}
return num == 1;
}
二、5698. 构成特定和需要添加的最少元素
题意:给一个数组,问数组最少追加多少个绝对值不大于 limit 的数字,可以使数组之和等于目标值 goal。
思路:求和、取模即可。
int minElements(vector<int>& nums, int limit, int goal) {
ll sum = accumulate(nums.begin(), nums.end(), 0LL);
ll dis = goal - sum;
if(dis < 0){
dis = -dis;
}
return (dis + limit - 1)/ limit;
}
5699. 从第一个节点出发到最后一个节点的受限路径数
题意:给一个加权无向连通图,求从节点 1 到节点 n 的路径个数。
假设路径为 [1,a,b,n],要求 a 到 n 的最短距离 大于 b 到 n 的最短距离。
思路:简单分析后,发现这道题很简单,而且一定存在答案。
第一步:构造出一个无向图。
第二步:计算每个节点到 n 的最短距离(单源最短路算法,bfs)。
第三步:根据每个点的最短距离,计算出一个有向拓扑图。
第四步:计算出节点 1 到 节点 n 的路径个数(bfs)。
对于第二步,计算单源最短路,使用经典的 Dijkstra 即可。
Dijkstra 算法的核心思想是,将节点分为三个集合,一个是已经确定最优最短路径的节点,一个是临时最短路答案,一个是未计算到的点。
-)起初状态,起点在临时集合,其他点都在未计算集合。
-)每次迭代的时候,以贪心的方法,从临时集合里找到路径最小的点,此时可以确定,这个点的路径是最优的。
-)然后,将这个最优点加入到最优集合,并扫描这个点的所有边,更新相邻掉的临时最短路径(如果在未计算集合,则加入到临时集合)。
-)这样不断迭代,最终起点可到达的点都会在最优集合里面。
当时,考虑到是是稀疏图,点的个数是2 * 10^4,默认的复杂度是O(n^2),会超时。
所以贪心找下个最小路径的点时,需要使用优先队列来优化。
对于 BFS 找最值,优先队列面临一个问题:怎么修改已经在队列里的值。
这个恰好在上次比赛《leetcode 第 230 场算法比赛》的第四题分享了。
简单来说,就是标记一下,遇到重复点时,能够识别出其他的是无效的。
单源最短路的代码如下:
void BfsVal(){
disVals.resize(n+1, INF);
min_queue<pair<ll, int>> que;
que.push({0, n});
unordered_set<int> s;
while(!que.empty()){
auto node = que.top(); que.pop();
int u = node.second;
if(s.count(u))continue;
disVals[u] = node.first; // 找到 u 的最优单
s.insert(u);
//printf("u=%d v=%lld\n", u, disVals[u]);
for(auto&p : m[u]){
int v = p.first;
if(s.count(v)) continue;
ll newVal = disVals[u] + p.second;
if(newVal < disVals[v]){
que.push({newVal, v}); // 有更优答案
}
}
}
}
求出了单源最短路,就可以遍历所有边,判断是否符合最短路的大小关系,不满足就删除。
从而可以得到一个所有节点指向节点 n 的有向无环图。
当然,也可以逆向思维,得到一个节点 n 出发的一个有向树。
最后就是从节点 n 出发,按照拓扑图,逆向的达到父节点的路径个数。
原理大概入下图,从后向前,每个出度为 0 的节点的路径个数就是所有儿子路径个数之和。
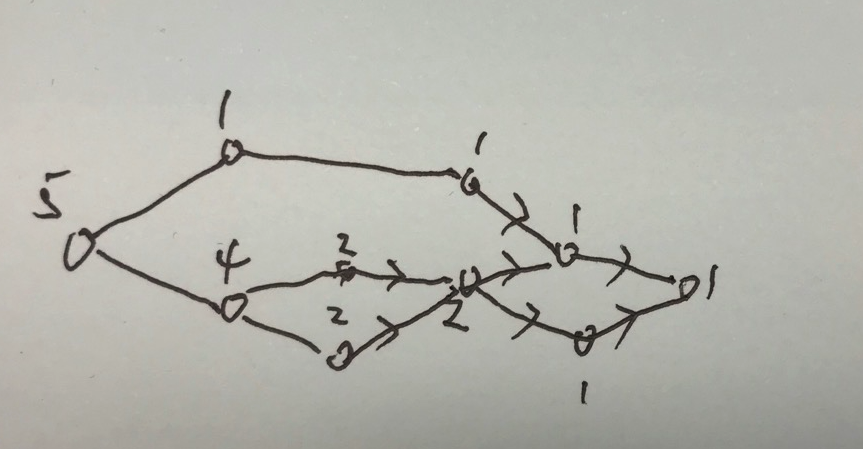
当然,由于已经有每个节点的最短路了,我们也可以直接使用这个最短路的值从小到大来一次计算节点的路径数(排序也可以)。
void BfsAns(){
min_queue<pair<ll, int>> que;
for(int i=1;i<=n;i++){
que.push({disVals[i], i});
}
ans.resize(n+1, 0);
ans[n] = 1;
while(!que.empty()){
auto node = que.top(); que.pop();
int u = node.second;
for(auto&p : m[u]){
int v = p.first;
ans[u] = (ans[u] + ans[v]) % mod;
}
}
}
四、5700. 使所有区间的异或结果为零
题意:给一个数组和一个整数 k,问是否可以修改数组若干位置的值,使得任意长度为 k 的连续子数组,所有数字异或得 0。
思路:首先可以推导出一个性质。
根据 XOR([1,k]) = 0 且 XOR([2,k+1]) = 0,可以得到最终 [1] = [1+k]。
推而广之,[i] = [i+k]。
所以我们需要先对数组按 k 进行分组,得到 k 组数字。
对于每组数字,我们可以讲数字修改为 [0,maxVal] 之间的任意值。
如果可以想到这里,我们就可以写出枚举的动态规划方程了。
遍历每一分组,枚举将值修改为任意值。
复杂度:O(k*2^10*2^10)
vector<int> dp(kMaxCol, kMaxVal);
vector<int> tmpDp(kMaxCol, n);
dp[0] = 0;
for(auto& col: grid){
int sumVal = accumulate(col.begin(), col.end(), 0);
tmpDp.clear();
tmpDp.resize(kMaxCol, kMaxVal);
for(int i = 0; i < kMaxCol; i++){ // 当前分组枚举修改为 i
int v = sumVal - col[i];
for(int j = 0; j < kMaxCol; j++){ // 前一个分组修改为 j 时的最优值
tmpDp[i^j] = min(tmpDp[i^j], dp[j] + v); //两个数字结合,可以得到的新值和最优值
}
}
tmpDp.swap(dp);
}
return dp[0];
这个复杂度其实是O(n^3),会超时的。
优化:
对于上面的分组,我们还可以得到两个性质。
性质一:保留一个数字,或者全部修改。
对于一组数字,要么修改为当前组内的某个数字,要么全部修改为其他数字。
性质二:最优解不可能同时修改两组的所有数字。
可以使用反证法证明这个结论。
假设第一组数字个数是 a1+b1,第二组数字个数是 a2+b2,其中 a 代表某个相同数字的个数,b 代表其他数字的个数。
令其他组修改了 c 个数字,则修改两组所有数字的修改数是 a1+b1+a2+b2+c。
而我们很容易构造出一种方案 a1+b1+b2+c 来,而且修改数比上面的更优。
具体修改是,第二组数字不用全部修改,只需要把b2个数字都修改为 a2代表的数字即可。
性质三:答案肯定存在两种情况内。
-)所有分组,都可以保留一个内部数字,即不需要全部修改。
-)有一个分组,所有数字全部修改。
对于第一组情况,可以通过枚举有效集合,动态规划来做。
均摊复杂度:O(n* 2^10)
vector<int> dp(kMaxCol, kMaxVal);
vector<int> tmpDp(kMaxCol, n);
dp[0] = 0;
for(auto& col: grid){
int sumNum = 0;
for(auto&p : col){
sumNum += p.second;
}
tmpDp.clear();
tmpDp.resize(kMaxCol, kMaxVal);
for(auto&p : col){
int i = p.first;
int num = p.second;
int v = sumNum - num;
for(int j = 0; j < kMaxCol; j++){
tmpDp[i^j] = min(tmpDp[i^j], dp[j] + v);
}
}
tmpDp.swap(dp);
}
这个与超时的暴力方法不同之处就是,修改的值,不再是枚举[0, 2^10),而是枚举当前分组的数字。
这样最外层两层循环合起来总共循环O(n)次,所以不会超时。
对于第二组情况,可以贪心来做。
均摊复杂度:O(n)
int minNum = n;
int oneAns = 0;
for(auto& col: grid){
int sumNum = 0, maxNum = 0;
for(auto&p : col){
sumNum += p.second;
maxNum = max(maxNum, p.second);
}
minNum = min(minNum, maxNum);
oneAns += sumNum - maxNum;
}
贪心原理:对于每个分组,保留数量最多的数字,这样可以得到一个修改总数。
此时可能异或后不是 0,需要选一个分组来全部修改。
那选择哪个分组呢?
假设选择了某个分组,修改的此时需要加上这个分组的最大数字个数(前面贪心的时候这些数字没有修改)。
想要总答案最小,显然,选择最大值最小的那个分组最优,因为这样需要增加的数量最少。
综合这两种情况,就可以得到最优值了。
五、最后
这次比赛前两道题是签到题。
第三题是综合性的图论题,涉及最短路、构造有向拓扑图,路径树三个知识点。
第四题则是比较复杂的动态规划,需要结合贪心来优化,避免枚举无效子集才能不超时。
最近校招的季节到了,leetcode 的比赛题难度加大了,感兴趣的可以来做一下。
加油,算法人。
《完》
-EOF-
本文公众号:天空的代码世界
个人微信号:tiankonguse
公众号ID:tiankonguse-code
本文首发于公众号:天空的代码世界,微信号:tiankonguse
如果你想留言,可以在微信里面关注公众号进行留言。
