2021 TPC 腾讯程序设计竞赛（1）

零、背景

2021 年 TPC 腾讯程序设计竞赛 又开始了。

4 月 13 号，周二晚上，参加了 2021 年 TPC 腾讯程序设计竞赛第一季第一场比赛。

PS：下午有会议，开会到 18:30，而比赛是 19:00 开始。
最终吃完饭回到座位时，已经 18:55 了。

我找一个空的电话亭后，Mac 电脑却卡死了。
第一次重启，会自动打开之前的程序，又卡死了。
第二次重启，禁止自动打开之前的程序，电脑才回复正常。

结果开始比赛的时候，外连的鼠标和键盘无响应了。
最后只好使用Mac 自带的键盘与触摸板来操作电脑了。

出师不利呀。

一、美丽序列

题意：给一个序列，当相邻两个数字的乘积不大于0时，称为美丽数列。
问是否可以重排列数列，得到一个美丽数列。

思路：相邻乘积不大于0，自然需要符号互斥。
而 0 属于万能数字，可以去适配任意符号。

所以思路就是优先使用正负符号匹配，剩下的使用 0 去匹配。
如果能够匹配上，就是美丽梳理。

正负符号匹配的规则也很容易想到，谁多谁在第一个。

if (abs(one - two) <= zero + 1) {
  printf("Yes\n");
} else {
  printf("No\n");
}

二、巧克力棒

题意：给 n 个正数字，问是否可以将一个数字 k 拆分为其他两个数字 a 和 b，使得a+b=k。
并且得到的所有数字不重复。

思路：首先，需要理解题意。
题意要求是所有数字不重复。

此时需要分情况讨论。

1）某个数字出现大于等于3次，此时不管怎么拆分，都会有重复，即无答案。
2）多个数字出现两次，拆分一个数字后，肯定还是会有重复，无答案。
3）只有一个数字出现两次时，此时必须拆分出现两次的这个数字。然后判断是否可以拆分。
4）没有数字重复，则枚举所有数字，判断是否可以拆分。

由于正整数的数据范围只有 1000，直接暴力枚举来检查是否可以拆分即可。
默认复杂度：O(n^3)
map优化：O(n^2 log(n))
hash优化：O(n^2)

注意事项：拆分的两个数字也不能相当。

bool check(int val) {
  for (int i = 1; i < val; i++) {
    if (m.count(i) == 0 && m.count(val - i) == 0 && i != val - i) {
      return true;
    }
  }
  return false;
}

三、完全平方数

题意：给两个数 n 和 k，问是否可以构造出长度为 n 的序列，使得序列中存在 k 个二元组，且二元组之和是完全平方数。
完全平方数定义：其平方根也是整数。
二元组：无序，即 n 个整数可以有C(n,2)个二元组。

思路：显然可以判断，当 k 大于 C(n,2)的时候，没有答案。

那问题是，k 不大于的时候，是否肯定可以构造出答案。

这时候只能枚举较小的 n 和 k，看答案都是怎么构造出来的。

-）k = 0，n 至少是 1，所有数字使用 1 即可。
-）k = 1，n 至少是 2，使用 2 * 2，剩下的数字使用 1 即可。
-）k = 2，n 至少是 3，使用 2 + 7 + 9 即可。
-）k = 3，n 至少是 3，使用 3 * 2 即可。
-）k = 4，n 至少是 4，使用 2 * 2 + 7 + 9 即可。
-）k = 5，n 至少是 4，使用 2 * 2 + 2 * 7 即可。
-）k = 6，n 至少是 4，使用 2 * 4 即可。
-）k = 7，n 至少是 5，使用 3 * 2 + 7 + 9即可。
-）k = 8，n 至少是 5，无解？

我手动模拟到 k = 8 的时候，发现构造不出答案来了。

我的推导原理如下图，关键靠 2 这个数字自身快速增加完全平方数。

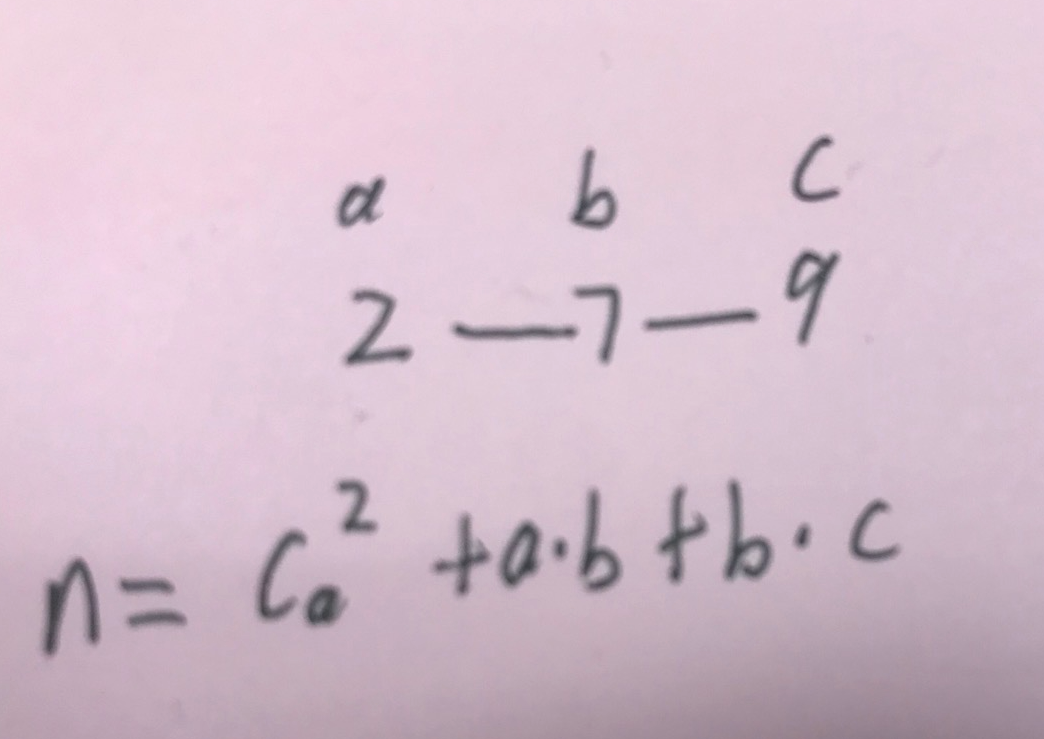
赛后，有人说需要找到两个像 2 这样的数字才行，比如 2 7 98。

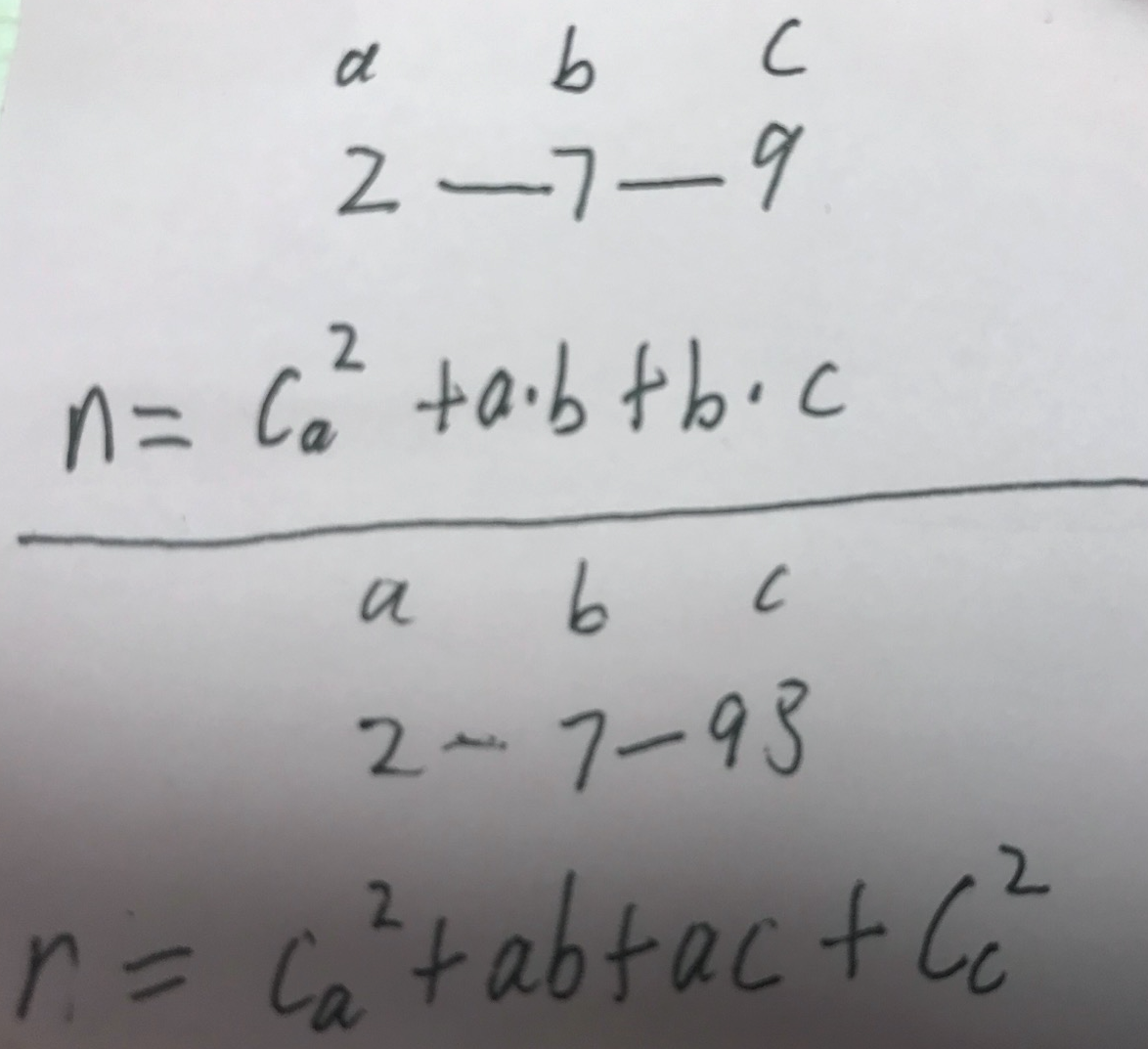
我听到这句话瞬间知道怎么做了。
比赛的时候有想过这个，当时我画出很多种组合，尝试列出所有方程，一个个去验证那个是答案。

这个想法没问题，就是我没这个耐心，因为后面还有两道题，下一道题过的人更多。

四、蚂蚁

题意：在横坐标轴上给 n 个蚂蚁的坐标。
为了报团取暖，蚂蚁每秒左右移动一个单位。
问最少过多少秒，每个蚂蚁方圆 d 单位内至少有一个蚂蚁。

思路：比赛的时候，有两个地方理解错了。

第一，我以为最终所有蚂蚁可以构成一个连续区间，即从左右到右，相邻蚂蚁的距离不大于 d。
赛后又读了下题，发现蚂蚁两两结合也是可以的，即最终蚂蚁分成了若干个连续区间，每个区间内蚂蚁报团取暖。

第二，我以为移动过程中，一旦距离在 d 范围内了，就不能再分开了。
赛后发现，这里只是要最终结果，不关心中间过程。

这两点确定了，就很容易想到二分做这道题，即判断指定时间能够满足答案。

那给了一个最大时间，怎么判断是否满足答案呢？

对于每个蚂蚁，枚举这个蚂蚁是左边界或不是左边界时可以向右到达的最远距离。

如果是左边界，最远距离就是 x + mid。
如果不是左边界，则判断这只蚂蚁能否和上一个蚂蚁报团取暖，可以了求出最远距离 min(pre + d, x + mid)。

枚举过程中，一旦遇到无法报团取暖，就代表当前时间太小，继续二分即可。

当然，和同事讨论这道题，说可以把上面的过程转化为动态规划。

我隐隐约约感觉确实可以，但是思维不够强大，心中还没想清楚。
周末后，纸上再画画，看能不能使用动态规划做。

五、棋盘上的数字

题意：给一个棋盘，有一些位置上有障碍物，其他位置都是数字 1。
现在对整个棋盘进行上下左右移动操作。

当向一个方向移动时，所有非障碍物位置都需要朝对应的方向移动一下。
数字移动出去后，如果没有数字移动过来，则对应的位置为数字 0.
如果数字前面是障碍物无法移动，则不进行移动。
如果某些数字移动到下个位置，下个位置不能继续移动，则那个位置的两个数字合并求和。

每次移动后，求所有合并数字的和。

思路：首先需要理解这道题，多读几遍边可以理解，发现就是也够大的模拟题。

每次移动复杂度：O(n^2)
有 q 次移动，总复杂度 O(n^2 * q)。
暴力模拟会超时。

看下数据范围，会发现障碍物是突破口，因为障碍物只有 n 个。

所以可以反向来做，每次移动的时候，相当于障碍物逆向移动。
对于四周，可以加一圈障碍物。

这样每次移动的时候，只需要计算障碍物周边的数字，复杂度O(n)。
综合复杂度O(n*q)

六、最后

这次比赛的题很好。

第一题构造题、第二题构造题，第三题构造题，第四题二分或者动态规划，第五题模拟题。

这么简单的题，我却只做出两道题。
下次比赛争取能做出三道题吧。

加油，算法人。

《完》

-EOF-

本文公众号：天空的代码世界
个人微信号：tiankonguse
公众号ID：tiankonguse-code