leetcode 第 245 场算法比赛

零、背景

正常的打比赛，第一题统计题、第二题二分、 第三题签到题、第四题动态规划。

其中最后一题有简单暴力的做法，也有正确但比较复杂的方法。

一、重新分配字符使所有字符串都相等

题意：给 n 个字符串，可以任意的挑选一个字符串，将其中的一个字符插入到另外一个字符串的任意位置。
问最终是否可以使得这 n 个字符串相等。

分析：既然可以对字符任意移动到任意位置，统计每个字符的个数是否可以整除 n 即可。

二、可移除字符的最大数目

题意：给两个字符串 s 和 p，p 是 s 的子序列。
现在给一个删除 s 的下标数组，问从前到后依次执行删除操作，最多可以删除多少个，依旧可以保证 p 是 s 的子序列。

分析：字符串长度是 10^5，删除数组也是10^5。
判断一个字符串是否是另外一个字符串的子序列复杂度是O(n)。
那暴力判断的复杂度就是O(n^2)

由于删除前缀只存在是子序列或者不是子序列，且一旦不是子序列后，之后必然都不是子序列。
这里就可以使用二分搜索来寻找最大值了。
复杂度：O(n log(n))

对于一个固定的删除前缀，也不需要真实操作原字符串。
只需要对前缀建立一个 hash 映射，快速判断是否跳过当前下标即可。

这里只分享下 check 函数。

bool checkOK(int mid){ // [0, mid)
    if(mid == 0) {
        return true;
    }
    h.clear();
    for(int i=0;i<mid;i++){
        h.insert(removable[i]);
    }
    
    int si = 0, sn = s.size();
    int pi = 0, pn = p.size();
    
    while(pi < pn && si < sn){
        if(h.count(si)){
            si++;
            continue;
        }
        
        if(s[si] != p[pi]){
            si++;
            continue;
        }
        
        si++, pi++;
    }
    return pi == pn;
}

三、合并若干三元组以形成目标三元组

题意：给一个三元组数组，问是否可以选择一些三元组，各自的位置取max，得到目标三元组。

思路：对所有不大于目标的三元组都取 max 即可。

四、最佳运动员的比拼回合

题意：给 n 个运动员有自己的编号。
每一轮有 n/2 回个，分别是第一个与最后一个，第二个与倒数第二个，依次递推。
如果 n 是奇数，则中间的那个人自动晋级。
这样每进行一轮，人数减半，剩余的人按编号站队，进行下一轮比赛，最后肯定可以得到冠军。

现在给你两个超级天才的位置，其他人都打不过这两个超级天才。
假设其他运动员的战斗力可以随意分配，问这两个天才最快需要几轮可以撞见对方，还需要求出最慢需要几轮。

分析：最快与最慢是相反的，只要回计算最快的，相同的方法就可以求最慢的。
所以这里我们只求最快的方法。

状态定义：dp[n][a][b]
状态含义：n 个人，一个位置在 a 一个位置在 b 的最优值。
由于编号的顺序每次都是升序，所以可以假设 a 永远小于 b。

状态转移分析：假设一轮比赛后，人数减半。
由于运动员依旧是按编号排序的，那相对位置不变。
编号可以重新映射为连续区间，答案依旧不变。

所以可以得到状态转移方程：

dp(n, a, b) = min(dp(n/2, ai, bi))  

其中 ai 与 bi 是剩余人中的相对位置，即重新映射的连续编号。

方法一：暴力枚举

两个天才的位置确定后，其他运动员之间谁都可能赢，所以每一轮共有 2^(n/2)中情况。

那我们可以枚举这些情况，求出最优值。
复杂度分析：2^14 * 2^7 * 2^4 * 2^2 * 2^1
复杂度：2^28

少做优化，这个方法就可以水过去。
看不少人都是这样水过去的。

方法二：优化

分析一下方法一的状态，发现很多状态都是重复计算。

比如有 2n 个人，转化为了 2 个人，两个天才顶多有 C(n/2, 2) 中位置。
人数固定了，位置固定了，答案也是固定的。
所以枚举的 2^n/2 中情况，有效的子状态只有 C(n/2, 2)个。

所以我们只需要枚举有效的子状态即可。

先只考虑偶数，根据两个天才的相对位置，可以分五种情况来讨论。

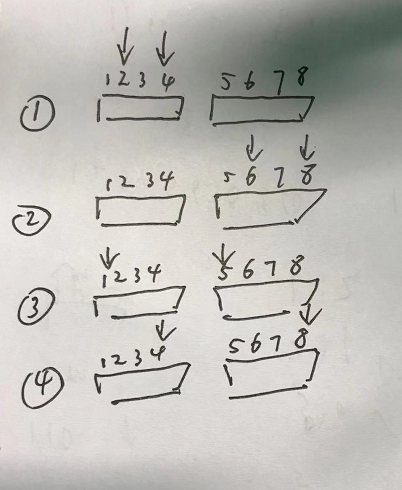
0、两个天才在相同位置（直接得到答案） 1、两个天才都在左区间。
2、两个天才都在右区间。
3、两个天才在不同区间，第一个天才靠前一些。
4、两个天才在不同区间，第二个天才靠前一些。

根据两个天才的相对位置，可以把区间分为三部分：两人左边、两人之间、两人右边。
分别枚举这三部分，就可以计算出子状态两个天才的相对位置，递归取最优值即可。

这里以第二种情况两个天才都在左区间为例来理解。

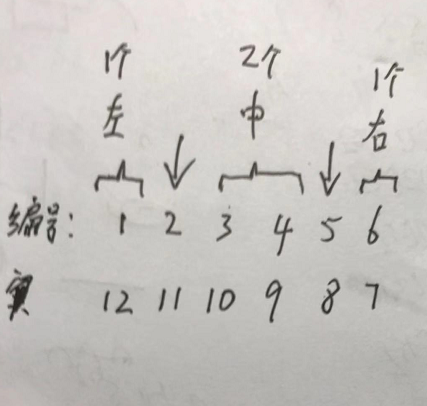
左部：第一个天才昨天有一对选手。
中间：两个天才中间有两对选手。
右部：第二个天才右边有一对选手。

对于左部，图中的上半部可以赢得个数可以是 0 个，也可以是 1 个。
对于中间，图中的上半部可以赢得个数可以是 0 个，也可以是 1 个，还可以是 2 个。
对于右部，图中的上半部可以赢得个数可以是 0 个，也可以是 1 个，不过不管几个，都不影响子状态。

假设枚举之后，第一个天才前面的人数是 左部的人数，第二个天才前面的人数是左部 加 中间的人数。

也就是说，对于情况二，我们只需要枚举左部和中间，即可得到所有的有效状态。

当然，对于其他情况，稍微复杂一些，这里就不展开讲了。
大家纸上画画应该就可以理解，都是一个道理。

代码： https://github.com/tiankonguse/leetcode-solutions/blob/master/contest/2/245/D.cpp

五、最后

这次比赛第二题就来一个二分，刚开始看到时有点不可思议。
然而看到第三题时，两分钟就过了，发现这题的顺序非常不合理。
到第四题，我本想暴力计算，后来想还是使用标准方法做吧，结果题意理解错了。

本来是第一个人与最后一个人对打的，我代码敲成第一个人与n/2+1个人对打。
后来测试样例没过，又花了好多时间来调整所有情况的左部、中间、右部的最大值。

总的来说，最后一题确实有韩都，你是怎么做这道题的呢？

加油，算法人。

《完》

-EOF-

本文公众号：天空的代码世界
个人微信号：tiankonguse
公众号ID：tiankonguse-code