atcoder abc 第 242 场算法比赛

零、背景

这周六正常参加了 atcode 的 abc 比赛，除了最后一题扩展题，其他题现在都会做了。

A - T-shirt

题意：参赛人员有机会发文化衫。
前 A 名保证发一件文化衫。
第 A+1 名到第 B 名会等概率抽奖的方式发 C 个文化衫。
现在你得了第 X 名，问获得文化衫的概率是多少。

思路：

如果是前 A 名，概率是 100%。
如果是滴 B 名之后，概率是 0%。
如果是抽奖区间，则概率是 C/(B-A)。

B - Minimize Ordering

题意：给一个字符串，对字符重新调整，求字典序最小的字符串。

思路：对字符串的字符从小到大排序即可。

C - 1111gal password

题意：求构造 N 位由 1 ~ 9 组成的正数，对于一个整数，相邻数字的差值不应该大于1。
问可以构造多少个满足要求的数字。

思路：典型的数位 DP。

转移方程如下：

f(n, x) = f(n-1, x-1) + f(n-1, x) + f(n-1, x+1)

D - ABC Transform

题意：给一个由 ABC 三个字母组成的字符串。
接下来不断对字符串进行替换，替换规则如下

A → BC
B → CA
C → AB

这意味着，替换一轮，字符串长度就翻倍。
问替换 T 轮后，第 K 个字符是多少。

数据范围：

T <= 10^18
K <= 10^18

思路：

由于替换一轮，字符串长度翻倍。
所以可以确定，第 T 轮的第 K 个字符，是由第 T-1 轮的 K/2 个字符转换得到。

知道了上一轮从哪个字母转化得到，再根据奇偶性，就可以知道当前轮的答案。

有了上面的结论，循环倒推，就可以求出答案。

虽然 K 很大，但是每次除 2，这样不超过 64 次就可以变为第一个字符。
第一个字符的答案是固定的，模三即可求出来。

E - (∀x∀)

题意：给一个长度为 N 的字符串 S，问满足长度为 N 且字典序不大于 S 的回文串个数。

思路：也算数位 DP 题型。

状态转移方程如下：

f(x, y) = a * 26 ^ b + f(x+1, y-1)
a 为小于 str[x] 的字母个数
b = (y - x) / 2

这里以 DCBAABCD 字符串来举例理解方程。

第一个字符，值是 D，小于的字母有 A~C， 之后的子串可以是任意值组成的回文串。
具体来说，每个字母分别为前缀的回文字符串个数 3^26 个。
而以 D 为前缀的回文字符串，需要根据第二位判断。

第二个字符，值是 C，小于的字母有 A~B，之后的字符串又可以是任意值组成的回文串。
具体来说，每个字母分别为前缀的回文字符串都是 2^26 个。 而以 DC 为前缀的回文字符串，需要根据第三位判断。

之后的依次递推。

F - Black and White Rooks

题意：给一个 N*M 的棋盘，其中有 B 个黑棋子，W 个白棋子。
现在需要把所有棋子摆放在棋盘上，要求每行每列不能同时摆放黑白棋。
问有多少种摆放方案。

思路：比赛的时候看错题意了，看懂后发现也不难。

由于黑棋与白棋不能相遇，所以可以枚举黑棋有 xb 行 yb 列，白棋有 xw行 yw 列，剩余的行和列都是空。

定义状态方程 F(x, y, k) 代表 x 行 y 列的矩阵，填充 k 个棋子，每行每列至少一个的方案数。

则这道题的答案就是：

C(n, xb) * C(m, yb) // 黑棋的矩阵个数
* F(xb, yb, B) // 一个矩阵的方案数
* C(n-xb, xw) * C(m-yb, yw)  // 白棋的矩阵个数
* F(xw, yw, W) // 一个矩阵的方案数

当然，上面的状态转移方程有四层循环。
其中内部两层循环可以进行优化。

1 <= xw <= n-xb
1 <= yw <= m-yb
sum(C(n-xb, xw) * C(m-yb, yw)  * F(xw, yw, W))
= C((n-xb) * (m-yb), W)
= f((n-xb), (m-yb), W)

f(N, M, w)的几何意义是在 N 行 M 列里面，任意摆放 W 个棋子的方案数。

这个公式合并的思想，有点类似于排列组合 A(n, m) = C(n, m) * m!

而对于 F(xb, yb, B)，计算起来稍微复杂点，无法直接计算。
需要先求出 f(xb, yb, B)，然后前去多计算的。

F 函数是每行每列至少一个，可以理解为填充满的矩阵。
f 函数是任意摆放，没有限制，可以理解为填充满的矩阵加若干空行空列。
所以 f 与 F 相比， f 是由 xb * yb 个 F 子矩阵组成的。

这样就可以得到两个公式的等价关系

F(xb, yb, B) = f(xb, yb, B) - 不满足的情况
不满足的情况 = F(x, y, B), 1 <= x <=xb & 1 <= y <= yb

完整的代码如下，看起来简洁多了。

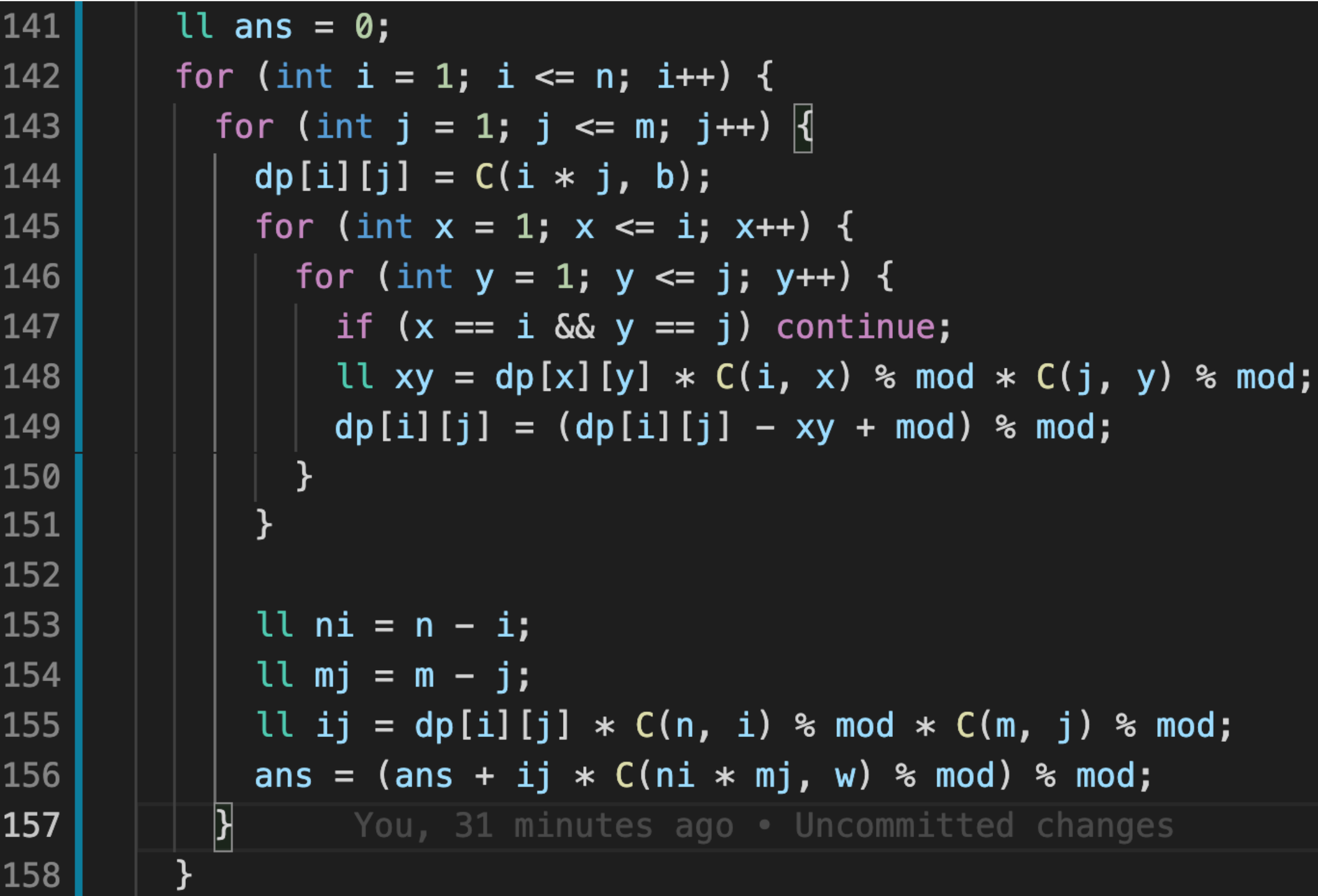
G - Range Pairing Query

题意：有一排有颜色的球，编号是 1 到 n。
有若干询问，问指定区间内相同颜色能够两两匹配的个数。

思路：询问的含义是先统计区间内所有求的个数，分别除二，再求和。

如果暴力做这道题，每次询问的复杂度是 O(N)
Q 个询问的复杂度就是 O(Q N)， 必然会超时。

这种区间询问的题型，是莫队算法的模板题。

莫队算法是一个离线算法，即记录下所有的区间查询。

莫队算法要求一个区间可以由相邻区间变换得到答案。

f(l, r) 
= f(l - 1, r) - F(l - 1)
= f(l + 1, r) + F(l)
= f(l, r - 1) + F(r)
= f(l, r + 1) - F(r + 1)

满足这个性质后，关键思路是分块。
一般按照查询区间的左边界划分为 sqrt(N) 个子块。
每个子块内的区间查询单独计算答案。

子块内，按右边界进行排序。

子块内的所有区间查询的右边界是不断变大的。
所以，一个子块内，右边界累计最多执行 O(N) 次转移。
所有子块合起来，右边界的复杂度就是 O(N sqrt(N))

子块内所有区间查询的左边界是不确定的。
所以，一次查询最多转移 O(sqrt(N)) 次。
所有查询合起来，复杂度就是 O(Q sqrt(N))

综合，复杂度依旧是 O(N sqrt(N)) 的量级。

八、最后

这次比赛题目挺好的。

比赛期间，我做出了前五题。
第六题看错题了，不看错的话，能不能做出来不知道。
第七题分块与莫队算法，学到新知识了。

最后的扩展题是概率期望题，面对概率题我从来都不会做，啥时候去研究下。

加油，算法人。

《完》

-EOF-

本文公众号：天空的代码世界
个人微信号：tiankonguse
公众号ID：tiankonguse-code