leetcode 第 338 场算法比赛

零、背景

这次比赛听说最后一题很难。
由于我家里有事，没参加这次比赛。
周日回深圳的时候就很晚了，周一晚上发高烧，周二也有点低烧，还是有必要补上题解。

一、K 件物品的最大和

题意：三个数值（-1、0、1）分别给若干个，问选择 k 个数字的最大值。

思路：优先取 1，接着取 0，最后取 -1。

二、质数减法运算

题意：给一个数组，可以对任意位置的值减去任意素数，问是否可以使得数组变为严格递增数组。

思路：贪心：优先把当前数字减的尽量小，但大于上一个数字。

具体实现：先筛出素数表，然后遍历数组，按照贪心规则计算即可。

暴力寻找素数，复杂度：O(n^2)
二分查找素数，复杂度: O(n log(n))

三、使数组元素全部相等的最少操作次数

题意：给一个数组，每次操作可以对一个元素加一或减一，问最少需要多少次操作，可以使得所有数字值相等。

思路：离线加离散化扫描计算即可。

先对数组值和查询值进行离散化，数据量 10^5。

先假设目标值都等于 0，答案就是数组和。
之后依次枚举离散化的值，并计算对应的答案。

计算转移公式：

ll dis = now - pre; // 上一个到当前值的距离
sum = sum - rightNum * dis + leftNum * dis
leftNum += counts[now];
rightNum -= counts[now];

四、收集树中金币

题意：给一个无向树，书中某些节点有金币。现在求一个子树，子树能覆盖所有金币。
覆盖定义：子树的每个顶点可以覆盖到距离为 2 以内的金币。
求节点数最小的子树。

思路：典型的树状 DP 问题，一个 DFS 搞定。

第一步：输入的边转为图。
第二步：递归，求出根为 0 时，各个节点的金币深度以及各个子树的最优答案。
第三步：DP 转移，将根节点从父节点转移到子节点，求出子节点为根的答案。

DP 转移分为的时候，需要把父节点的反向金币深度 和父节点的反向子树最优答案传下来。

void Dfs(const int now, const int pre = -1,
    const int preDep = 0, const int preAns = 0);

有了这个入参，子树为根的答案就可以直接计算出来。

childAns = max(1, coinAns0[now]) + preAns;

如下图，根转移到子树时，转移公式稍微有点复杂。

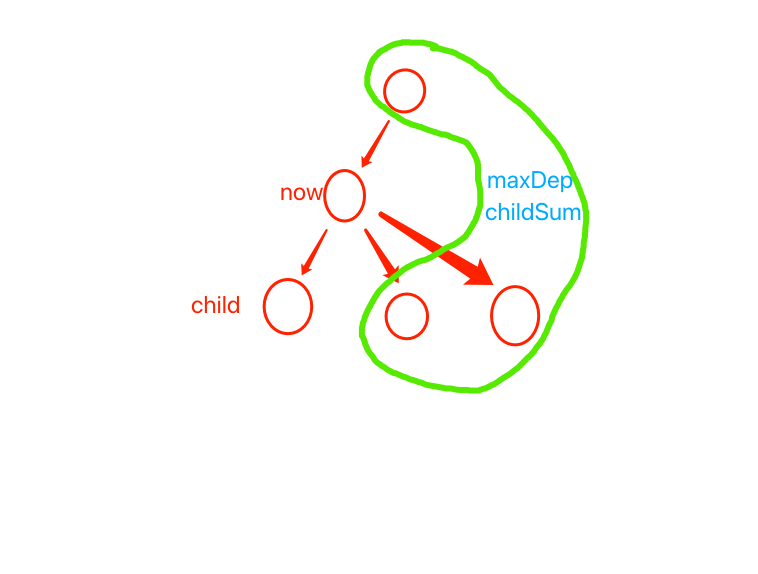
假设当前我们需要转移到 child 节点，就需要计算出 child 的 preDep 和 preAns。
而这个依赖与 now 节点的父节点子树 以及非 child 儿子节点，如上绿线圈起来的部分内容。

父节点的 preDep 和 preAns 函数参数中有，所以我们需要计算出非 child 儿子节点中的最大 dep 和累计答案。

暴力计算的话，可能会超时（根有 1 万个儿子）。
一般需要预处理出所有儿子的深度统计以及累计答案和，具体计算 child 的时候，再减去当前的 child 信息即可。

// 递归求子树的答案
Stat m;
int childSum = preAns;
for (auto v : g[now]) {
    if (v == pre) continue;

    m.Add(coinDeps[v]);
    childSum += coinAns0[v];
}


for (auto v : g[now]) {
    if (v == pre) continue;

    m.Del(coinDeps[v]);
    childSum -= coinAns0[v];

    int childMaxDep = preDep;
    if (m.Size() > 0) {
        childMaxDep = max(childMaxDep, m.QueryMax());
    }

    ...


    m.Add(coinDeps[v]);
    childSum += coinAns0[v];
}

当前根的其他儿子统计信息都得到了，就可以根据最大深度来判断了。
这里统计信息我使用 map 实现的。

大概分三种情况:
1、最大深度大于等于 2,此时根节点必须选择。
2、最大深度为0，此时根据当前根节点是否有金币判断。
3、最大深度为 1，则深度加一。

// 金币距离大于等于 2，必须选择当前根
if (childMaxDep == 0) {  // 长度为 0 或 1
    if (coins[now]) {
        childDep = 1;
    } else {
        childDep = 0;
    }
} else if (childMaxDep == 1) {
    childDep = childMaxDep + 1;
} else {
    childDep = 3;
    childAns = childSum + 1;
}

DfsAns(v, now, childDep, childAns);

五、最后

这次比赛最后一题有点难度，以往的树状DP都是很容易就状态转移，这次由于有两层的限制，转移稍微复杂一些。

思考题：2 层限制修改成 k 层，该如何做呢？

《完》

-EOF-

本文公众号：天空的代码世界
个人微信号：tiankonguse
公众号ID：tiankonguse-code