leetcode 第 339 场算法比赛
作者: | 更新日期:
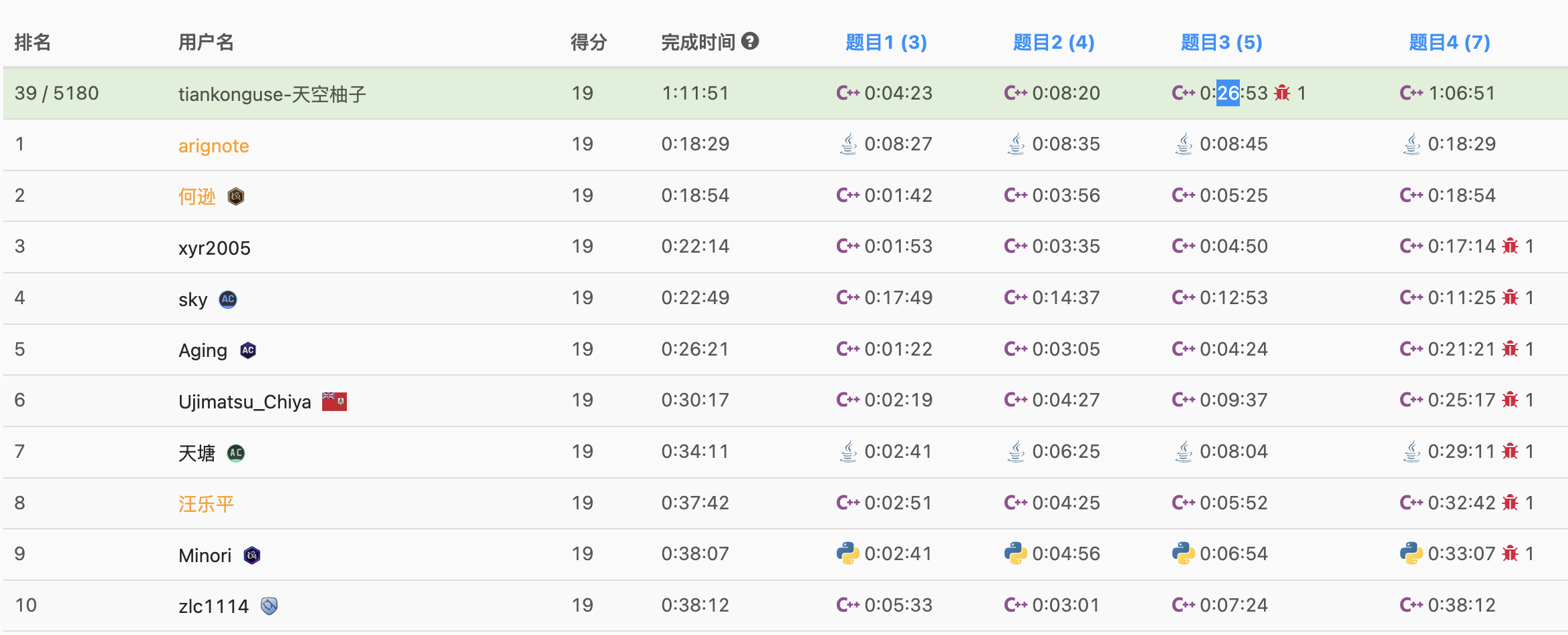
本以为做的太慢了,竟然 38 名。
本文首发于公众号:天空的代码世界,微信号:tiankonguse
零、背景
这次比赛感冒还没好,头昏沉沉的,另外我看错题了,浪费了不少时间,本以为要排名四五百名了。
一看榜单,排名 38(赛后39名),开玩笑,大佬今天都去参加其他活动了吗?
比赛源代码地址:
https://github.com/tiankonguse/leetcode-solutions/tree/master/contest/3/339
一、最长平衡子字符串
题意:给一个 01 字符串,求一个最长的子串,使得子串前一半都是 0 后一半都是 1。
方法1:动态规划动态统计法。
维护一个状态,代表当前在统计 0 还是 1。
如果在统计 0,遇到 0, 0 的计数加1。
如果在统计 0,遇到 1,状态改变为 1,更新答案。
如果在统计 1,遇到 1,1 的计数加 1,更新答案。
如果在统计 1,遇到 0,统计重置,状态改变为 0。
方案2:暴力循环。
数据范围只有 50,枚举起始位置,找符合要求的最长前缀。
二、转换二维数组
题意:给一个数组,要求划分为若干个子数组,使得每个子数组中元素不同。
思路:统计元素出现最多的个数,就是子数组的个数。
每个元素出现几次,就打散到几个子数组中即可。
三、老鼠和奶酪
题意: n 个盒子,盒子里有红球和篮球。
每个盒子只能取一个球,每个球有自己的得分。
问恰好取 k 个红球时,最大得分是多少?
思路:显然,求全取了分最高。
所以恰好取 k 个红色,则可以取 n-k 个篮球。
起初看错题了,每个球得分最大 1000, 看错为球的个数是 1000。
就敲了一个两层循环的动态规划,浪费二十分钟。
TLE 后,就推导怎么贪心来做这道题。
对比两个盒子的两种选择,可以发现, 红球与篮球差值越大,选择红球会更优。
故按红球与篮球的差值排序,最大的 k 个差值取红球,剩余的取篮球即可。
四、最少翻转操作数
题意:给一个数组,只有一个位置是 1,其他位置都是 0。
现在我们可以不断的操作选择一个长度为 k 的子数组,来反转这个子数组,使得 1 的位置发生变化。
不过有个限制,输入中明确要求,某些位置 1 不能反转到达。
问无限次操作后,哪些位置会有 1,以及变为 1 的最少操作次数。
思路:简单的 BFS 广度优先搜索即可。
分析可以发现,可以发现两个规律。
1)奇偶性规律。
当 K 为偶数时,反转后位置的奇偶性发生反转。
当 K 为奇数时,反转后位置的奇偶性不变。
2)反转范围规律
假设反转数轴无限长,则反转可以到达 K 个位置。
分别是从 p - k + 1 到 p + k - 1,步长为 2。
由于数组是有限的,我们需要对左右边界进行修正,得到合法的边界。
有了上面的两个规律,我们就可以 BFS 来做这道题了。
做之前,先思考一个问题:告诉你一个位置 P,以及可以到达的范围 [L, R]+2,该如何快速找到这个范围的答案呢?
直接遍历范围 [L,R] 显然可能会超时,例如范围内只剩一个有效数字,依旧遍历一遍,性价比太低。
答案是直接在有效数字上遍历即可。
所以我们需要维护一个分奇偶性的有效数字集合,通过二分查找快速找到左边界,然后遍历求出所有答案。
使用 cpp STL 的 set 这个数据结构,轻松实现上面的功能。
auto it = s.lower_bound(L);
while (it != s.end() && *it <= R) {
int v = *it;
ans[v] = ans[p] + 1;
que.push(v);
s.erase(it++);
}
五、最后
这次比赛很奇怪,第三题我浪费了几十分钟,竟然还能进 39 名。
你做出几道题呢?
《完》
-EOF-
本文公众号:天空的代码世界
个人微信号:tiankonguse
公众号ID:tiankonguse-code
本文首发于公众号:天空的代码世界,微信号:tiankonguse
如果你想留言,可以在微信里面关注公众号进行留言。
