leetcode 第 360 场算法比赛

零、背景

这次比赛最后一题一开始解法想错了，比赛结束后才通过，遗憾。

这次比赛四道题的代码：https://github.com/tiankonguse/leetcode-solutions/blob/master/contest/3/360

一、距离原点最远的点

题意：一个物体起始位置在数轴原点，给一个左右移动字符串，问最后的位置最远可以到达哪里？

移动规则：L 代表左, R 代表右, _代表可左可右。

思路：维护一个当前时刻可以到达的坐标集合，求出下个时刻的坐标集合。
集合大小：不超过移动次数。
复杂度：O(n^2)

二、找出美丽数组的最小和

题意：求构造一个长度为 n 的数组，数组中不存在二元组的和等于 k。求符合要求的最小数组和。

与上次比赛的题目一模一样，可以参考上次比赛的题解《leetcode 第 359 场算法比赛》。

算法1：循环计算。
复杂度：O(n)

算法2：数学计算。
复杂度：O(1)

三、使子序列的和等于目标的最少操作次数

题意：给一个数组和一个目标，数组中的值都为 2 的幂。
现在可以随机选择数组中的一个数字一拆为2个，大小相等。
问最少拆分几次，可以在数组中选出若干数字，和为目标。

思路：枚举目标每一位，求解即可。

第一步：预处理数组，统计每个幂数出现的次数。
第二步：从小到大找处理每个二进制位。
第三步：如果二进制位是1，看是否有对于的幂数，有了减一，没有也减一（后面会处理借位）。
第四步：当前二进制位剩余的幂数合并传递给高位。如果是正数，向下取值进正位，如果是负数，也向下取值进负位,代表需要拆分数字。

注意事项：数组之和小于目标时，是没答案的，否则肯定有答案。

对于借位，也可以直接向后循环寻找第一个非0的高位，实时计算借位。

四、在传球游戏中最大化函数值

思路：给一个数组，值为数组中的某个下标，代表这个位置可以把球传给值对于下标的位置。
现在问如何选择起始下标传球，才能使得传 k 次路径的下标和最大。

思路：图论题。

枚举所有可能，发现这是一个有向有环非联通图，对于每个联通分支，有且只有一个环。

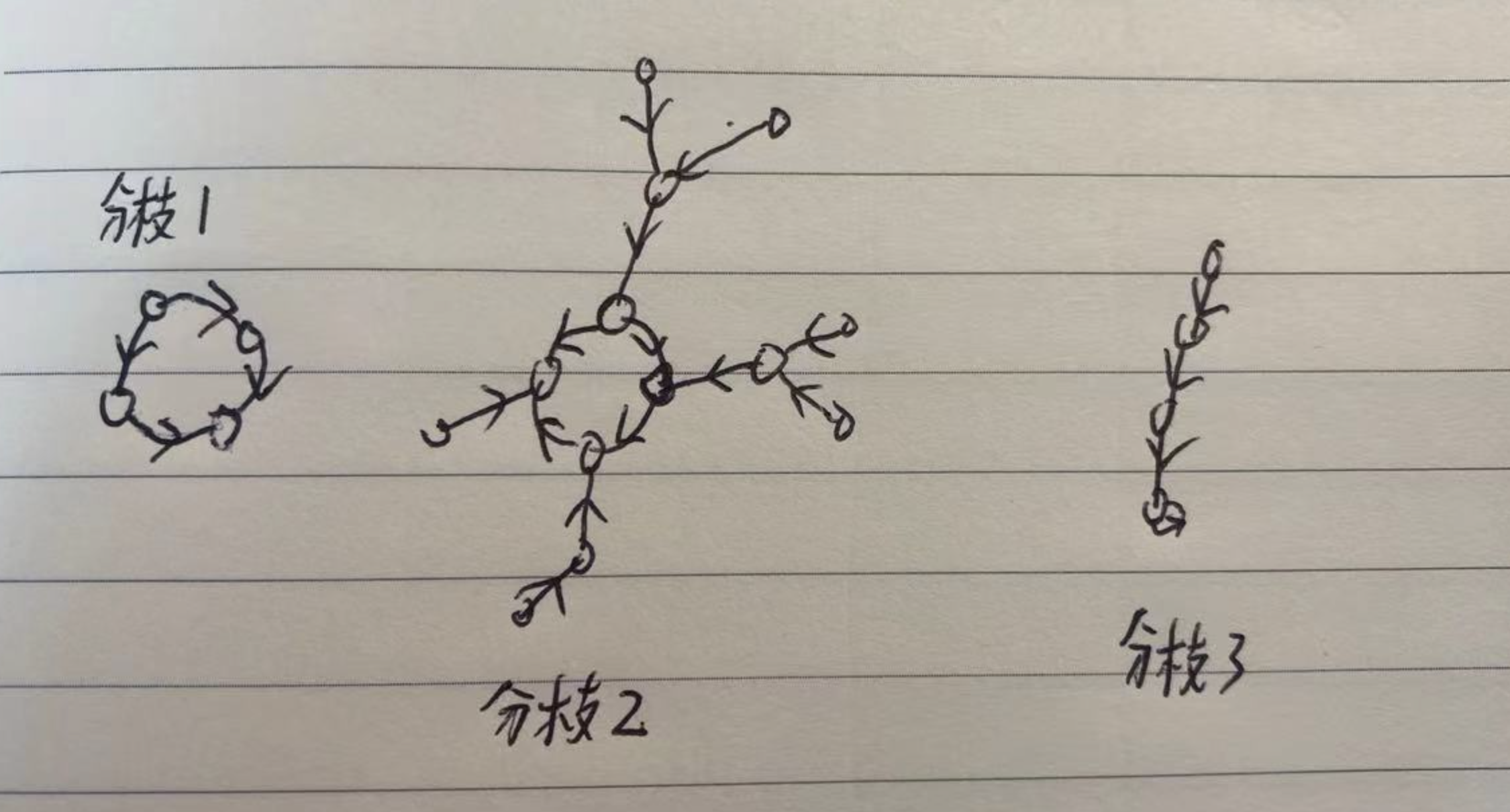
最复杂的图大概长下面的样子

第一种联通分支是一个环。
第二种联通分支最复杂，环的每个节点都有一个反向的有根树。
第三种联通分支是是环只有一个顶点，变成了一条链。

当然，第一种和第三种都是第二种的特殊情况，所以我们只需要考虑第二种情况如何处理即可。

很显然，如果起点在环上，转圈走 k 步即可。
如果起点不在环上，就是在某个反向有根树上，先走若干步到达根节点，即环上，之后按在环上处理即可。

所以我们需要预处理输入数组，构造一个数据结构，找到所有的环，以及环外的反向有根树。
这样就可以做这道题了。
复杂度：O(n*k)

不做优化，显然会超时。
所以需要预处理，进行快速计算。

对于环，我们需要预处理出环的前缀和，以及每个点在前缀的位置，就可以快速计算走 k 步的答案。

对于环外的反向有根树，起初很容易想到可以预处理出每个顶点到根节点的步数，从而可以快速走到环上，从而快速计算出答案。
但是如果 k 步无法到达环上又该如何处理呢？

对于这个有多种方案。
一种是通过 RMQ 倍增算法离线预处理。
一种是维护根到节点的前缀和数组，通过前缀相减即可得到区间和。

我是通过维护前缀和来做这道题的。
对于一个反向有根树，从根节点开始递归，即可计算出整个树上所有节点的答案。

代码比较复杂，大家具体可以参考源代码，代码敲完一下就通过了。
https://github.com/tiankonguse/leetcode-solutions/blob/master/contest/3/360/D.cpp

注意事项：k 是走 k 步，计算前缀和时，需要加一。

五、最后

这次比赛第三题敲错一个地方，浪费了几十分钟。

第四题一开始没想那么复杂，认为只有简单环，敲了半个小时，第一个样例没通过。
调试十几分钟，发现 k 需要加一。

再之后发现还需要考虑环节点上的反向有根树。
于是重新看题意，重新敲，时间就不够了。

这几道题你都是怎么做的呢？

《完》

-EOF-

本文公众号：天空的代码世界
个人微信号：tiankonguse
公众号ID：tiankonguse-code