leetcode 第 411 场算法比赛

零、背景

这次比赛依旧没参加，最后一题我想错方向了，最后看了一眼题解，才知道怎么做

A: 暴力枚举。
B: 简单动态规划。
C: 数位DP。
D: 滑动窗口+二分+前缀和。

排名：无
代码地址： https://github.com/tiankonguse/leetcode-solutions/tree/master/contest/4/411

一、统计满足 K 约束的子字符串数量 I

题意：给一个二进制字符串，问存在多少个子串，0和1的个数都不同时超过 k 个。

思路：数据量只有 50 个，枚举所有子串，统计 01 的个数，判断是否满足要求。

复杂度：O(n^3)

优化：固定起始位置的子串，下个子串可以复用上个子串的统计信息。
复杂度：O(n^2)

二、超级饮料的最大强化能量

题意：有两种有能量值的饮料，每次只能喝一种饮料。
另外，如果从一种饮料切换到另一种饮料，需要等待一个时刻。
问如何选择，最终喝的累计能量值最大。

思路：简单动态规划。

状态定义：dp(i, t)
含义：i 时刻喝 t 饮料时，能得到的最大能力。

状态转移: dp(i, t) = max(dp(i-1,t), dp(i-2, T)) + V[i][t];
含义：要么上个时刻喝相同的饮料，要么上个时刻等待，上上个时刻喝不同的饮料。

复杂度：O(n)

三、找出最大的 N 位 K 回文数

题意：求构造一个最大的长度为 N 的数字，该数字可以整除 K。

思路：由于 K 只有 9个数字，很容易想到去找规律。

例如几个数字很容易找到规律:

1: 9.......9
2: 89.....98
3: 9.......9
4: 889...988
5: 59.....95
6: 无规律
7: 无规律
8: 8889.9888
9: 9999.9999

6 再深入分析，发现其实还是有规律的，分为奇偶性。
偶数长度为 89.989.98
奇数长度为 89.9779.98

而对于 7，也是有规律的，不过需要区分的情况更多了。

另外，如果 N 较小时，上面的规律也不满足，需要特殊处理。
所以走枚举这条路风险很大，很容易遗漏某种情况。

其实，这道题是经典的数位 DP 题型。

状态定义：dp(i, m)
含义：前 i-1 个位置填充数据之后，前 i-1 个位置 与 后 i-1 个位置取模 k 后剩余为 m 时， 下个位置最大的存在答案的值。

状态转移方程如下：

dp(i, m) = -1 默认不存在答案
dp(i, m) = max(v if dp(i+1, M)>=0);

接下来看几个如何得到 m。

最开始，没有前缀和后缀，所以 m 等于 0。
假设第 i 位填充 v，取模满足分配率，可以推导出

r = i
l = n - 1 - i
M = (v * 10^r + v * 10^l + m) % k

枚举 v 的时候，从大到小枚举即可。
复杂度：O(n * k^2)

四、统计满足 K 约束的子字符串数量 II

题意：给一个二进制字符串，有多个询问，问一个区间内存在多少个子串，0和1的个数都不同时超过 k 个。

思路：6种算法。

算法1：枚举询问，枚举子串，统计01个数，判断答案。
复杂度：O(n^4)

算法2: 算法1基础上，相同前缀的子串，复用统计信息。
复杂度：O(n^3)

算法3: 反向思维。
题意要求两个都不超过 K，等价与所有子串 减去 两个都超过 k 的子串。
对于起始位置固定的所有前缀字符串，一旦找到第一个都超过 k 的子串，之后的子串也都满足要求。

预先统计所有前缀 [0,i] 的 0 与 1 个数 count[0/1][i]。

假设询问的是 [l,r]， 枚举每个位置 i 为起始位置，其中第一个满足要求的 0与1 的个数预期为 count[0/1][i-1] + k + 1。
这个可以通过二分查找 count[0/1] 找到，不妨设为 c， 则答案为 max(r-c, 0)。
复杂度：O(n^2 log(n))

算法4：反向思维 + 索引优化。
反向思维算法中，通过二分查找count[0/1]指定值的下标。
值与下标的关系可以预处理储存在数组中，这样就可以O(1)找到下标了。
复杂度：O(n^2)

一种错误的前缀和优化算法，导致走进死胡同。

反向思维基本逻辑是遍历每个询问区间，枚举区间内每个位置，一把计算出这个位置为起始位置的子字符串的答案。
枚举每个位置是 O(n) 的复杂度，必然会超时。

很容易想到如果有某个算法可以求出前缀区间 f(p) 的答案，则可以通过两个前缀求差得到区间的答案 f(r)-f(l-1)。

但是又一想，上面的前缀减法不对。
还存在部分子串穿过 l 左右边界的，这部分子串不在 f(l-1) 里面。

所以还需要定义一个状态：f1(p) 含义：p 左边至少有一个字符的所有满足要求的答案。

但是再一想，新的状态又多计算了。
例如对于子串 [l-1, r+1] 满足 f1(l) 的定义，但是不应该计算在内。

所以还需要减去所有覆盖 [l-1,r+1]的子串。

这样推导下去，发现没有尽头了。
就这样我想了一天，没想出解法。

算法5：坐标系法

第二天看了题解，发现应该分析O(n^2)算法的特征，找出规律，然后再降低复杂度。

反向思维基本逻辑是遍历每个询问区间，枚举区间内每个位置，一把计算出这个位置为起始位置的子字符串的答案。
如果我们预处理出计算整个字符串每个位置为起始位置的答案，则可以画出一条曲线。

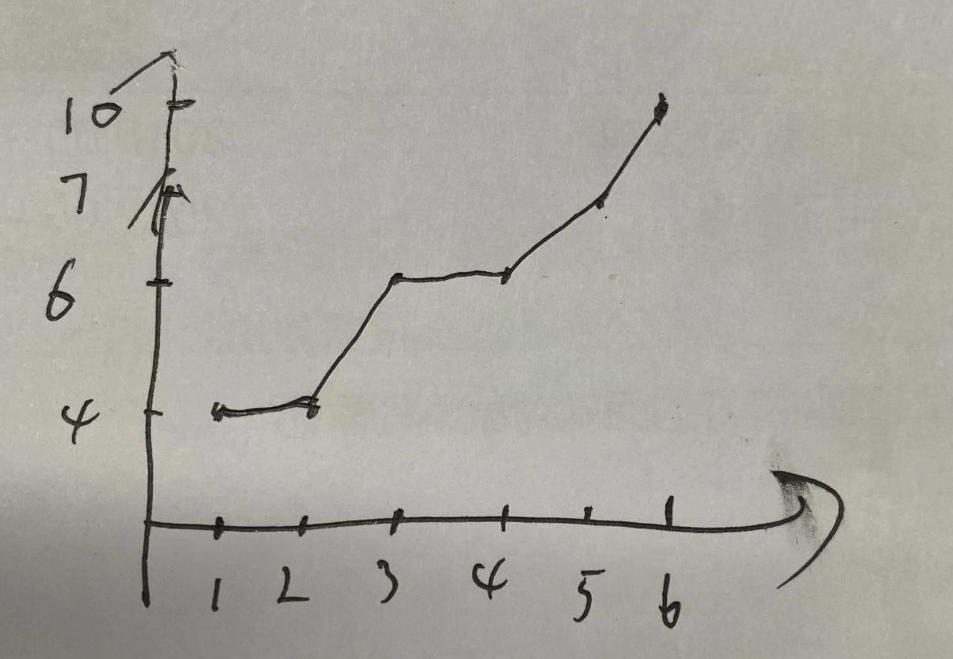
假设要求区间 [2,6]的答案，可以发现，[2,4]为起始位置的所有答案子串都不超过6，所以都是答案。
而对于[5,6]为起始位置的答案大于6，需要进行截断。

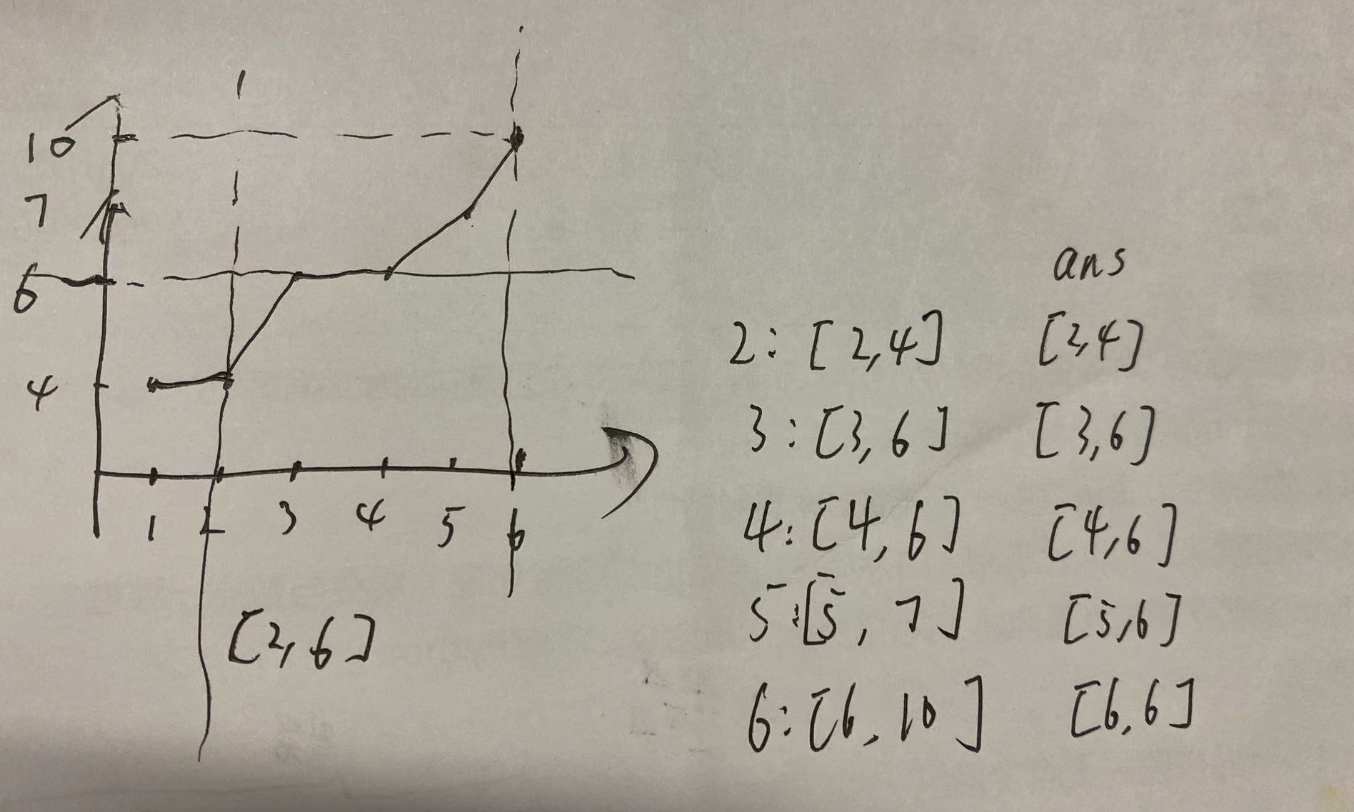
在图上展示出来，就是求坐标系中单杠阴影部分的面积。
而单杠阴影的面积等于整个阴影部分的面积 减去 下方双杠梯形的面积。

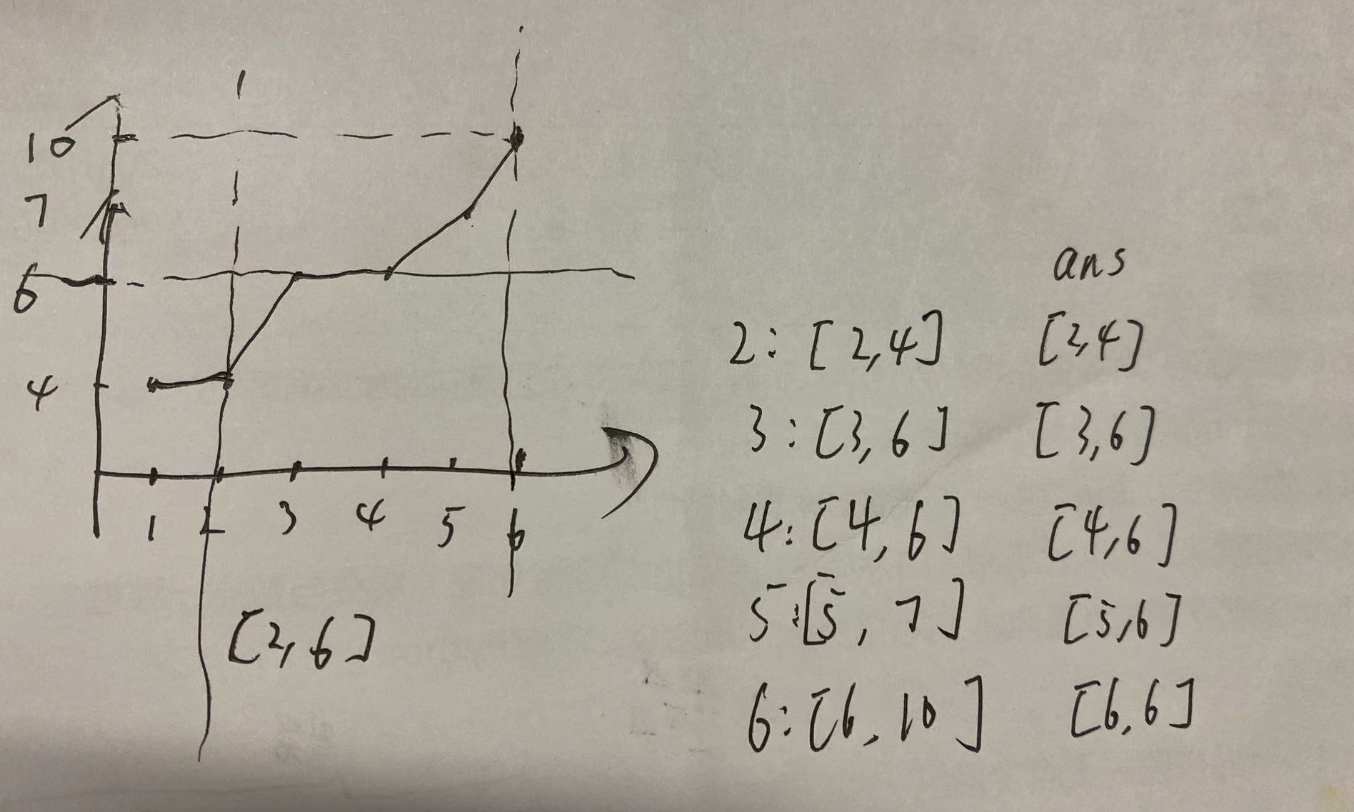
整个阴影部分的面积分为两部分。
其中，[2,4]的答案可以通过前缀和求差得到。
而 [5,6] 的答案，则是长方形的面积，直接可以计算得到。

现在的问题是，如何找到这个边界，即左半部使用前缀和计算，右半部使用长方形计算。
可以发现，曲线是单点递增的，所以可以二分查找。

就这样，就可以做出这道题了。 复杂度: O(n log(n))

算法6: 索引优化

坐标系法通过求面积，计算出了答案。
其中找分界线时，使用了二分查找。
其实这个二分查找也可以通过预先建立反查索引，通过可以做到O(n)找到目标。

复杂度：O(n)

五、最后

这次比赛最后一题最终有 6 个算法，复杂度从 O(n^4) 一步步优化到 O(n)。

而且，在去掉 O(log(n)) 的优化中，还发现如果二分查找，都可以通过建立索引的方法，来做到O(1)查找。

《完》

-EOF-

本文公众号：天空的代码世界
个人微信号：tiankonguse
公众号ID：tiankonguse-code