leetcode 第 414 场算法比赛

零、背景

这次比赛第三题想复杂了，浪费不少时间，结果第四题时间不够了

A: 简单计算。
B: 二分。
C: 贪心。
D: 博弈+状压。

排名：200+
代码地址： https://github.com/tiankonguse/leetcode-solutions/tree/master/contest/4/414

一、将日期转换为二进制表示

题意：给一个日期，要求把年月日转化为没有前导零的二进制。

思路：提取出年月日数字，转化为二进制字符串，拼接起来。

二、范围内整数的最大得分

题意：给一个数组区间，区间大小固定为d，每个区间内选择一个数字，所有数字之间的最小间距称为得分。
问如何选择区间的数字，使得得分最大。

思路：区间大小固定，可以对区间排序，使得区间为递增序列。
显然，最终选择的数字是单调非递减序列，且第一个数字选择区间的最小值，最后一个数字选择区间的最大值。

最小值中求最大，显然是需要二分的。
二分最小值，遍历区间，相邻区间取满足要求的最小值，判断是否都可以找到一个数字。

注意事项：二分的最大值为区间的最大值，即maxVal + d。

三、到达数组末尾的最大得分

题意：给一个数组，告诉你数组移动的规则，求从第一个位置移动到最后一个位置的最大得分。
规则：位置i移动到位置j，得分为 (j - i) * nums[i]。

思路：分析三个数字的关系，可以找到一个规律。
递增是都选择，递减时直接忽略中间的。

上面的其实就是求一个严格单调递增序列，按公式计算即时答案。

其实这个规律存在一个几何面积的性质，选择的相邻两点是一个矩阵面积。

相邻三个点递增时，选择中间的点如左图，不选择如右图，选择中间的点后面积更大。

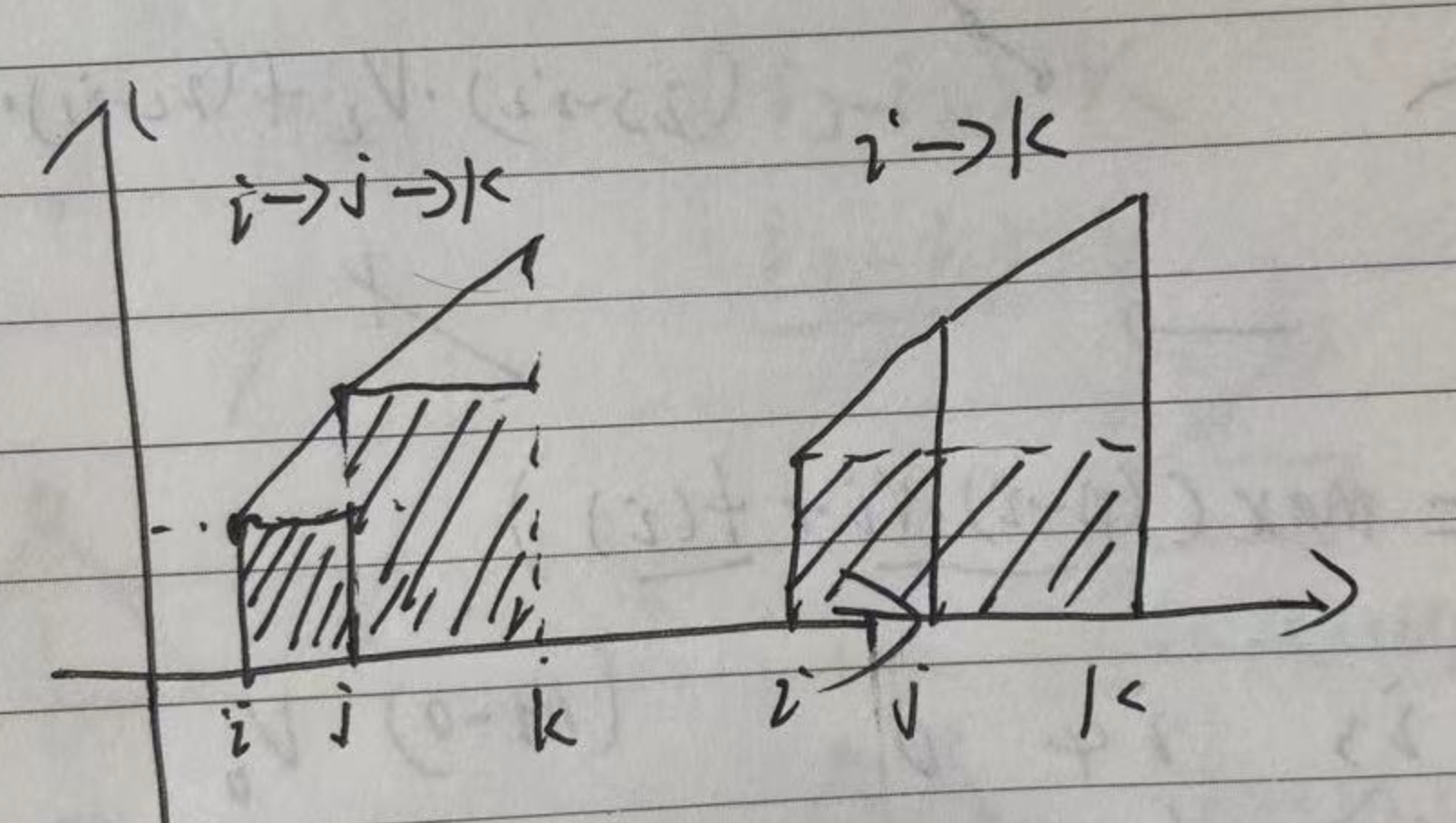
相邻三个点递减时，选择中间的点如左图，不选择如右图，不选择中间的点面积更大。

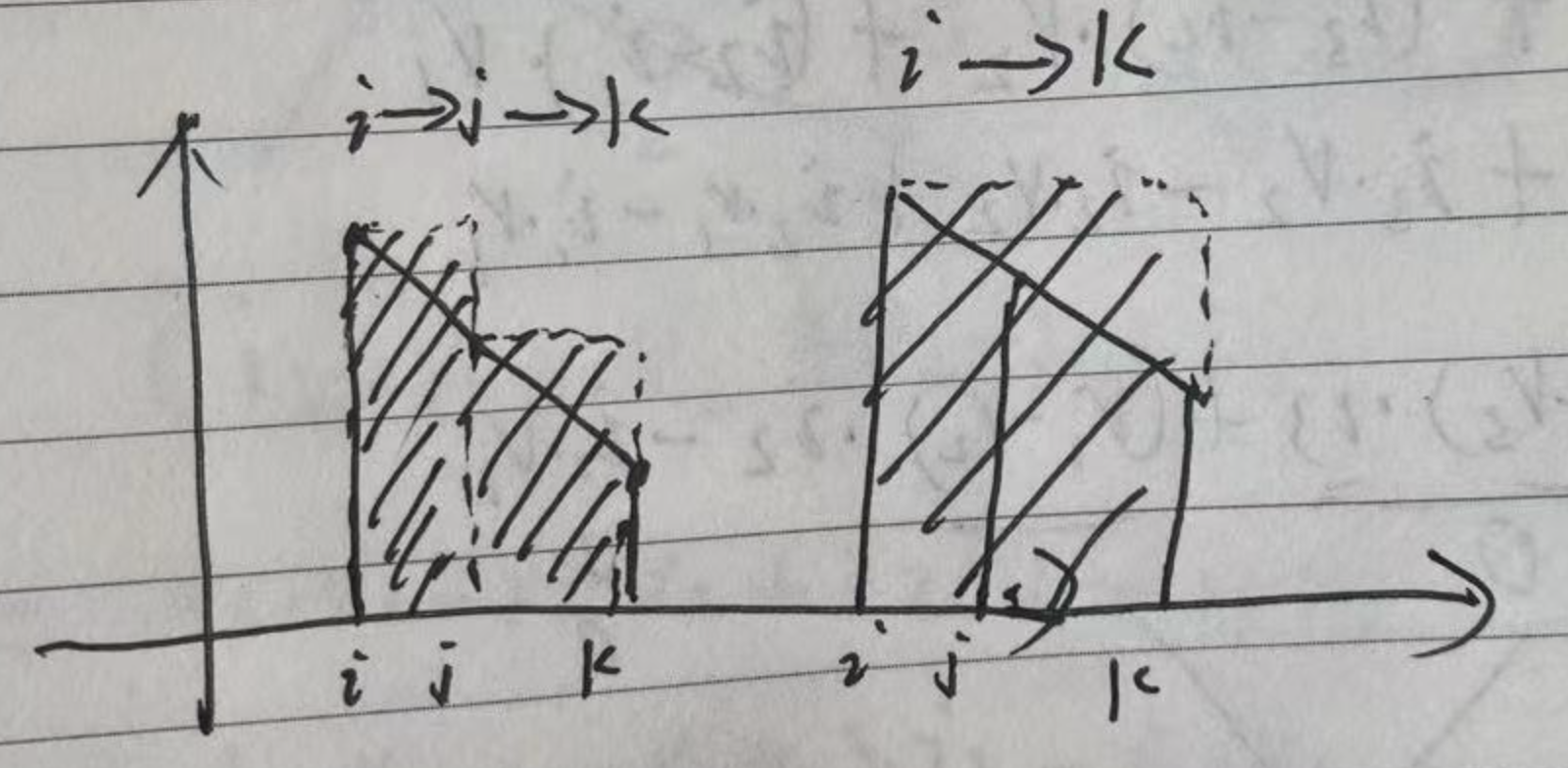
四、吃掉所有兵需要的最多移动次数

题意：给一个50*50的棋盘，以及一个马和若干兵棋子。
Alice 和 Bob 轮流使用马随意最优策略吃掉一个兵棋子，问 Alice 先走时，最大的移动次数。
确定兵棋子位置后，移动步骤固定，为从一个位置到另一个位置的最小移动步数。
Alice 策略：选择最优的兵，使得总移动次数最大。
Bob 策略：选择最优的兵，使得总移动次数最小。

思路：博弈+状压。

状态定义：dp[role][pos][mask]
含义: 角色为role，马的位置为 pos，兵的个数为mask时，role的最优答案。
只有15个兵，马的位置有16中情况，2中策略，故状态总个数为2 * 16 * 1<<15。

状态转移方程：
合并子状态时，Alice 取最大值，Bob 取最小值。

role = Alice
  dp[role][pos][mask] = max(Dis(pos, i) + dp[~role][i][mask^i])

role = Bob
  dp[role][pos][mask] = min(Dis(pos, i) + dp[~role][i][mask^i])

Dis 函数为从棋盘一个位置移动到另一个位置的最小移动步数，可以预处理计算得到。

注意事项：预处理 Dis 时必须使用50*50的棋牌进行计算。
不能通过坐标系横移的方法进行转换，因为边界不满足横移条件。

五、最后

这次比赛代码量比较大，比赛期间失误多次。

第二题二分时，一开始写的是相邻区间至少要有一个区间是二分值，导致自己构造的用例未通过，调试半天。
调试通过后，提交代码后，WA一次，原来最大值忘记加上 d 区间。

第三题一开始只考虑了递减的情况，得到的规律是找到最大值即可。
代码写完了，样例未通过，发现递增时不能忽略。

第四题计算任意两个位置的最小步数时，考虑的是计算原点到所有位置的最小步数，然后通过平移转换为任意两点的答案。
提交后WA一次，随后比赛结束了。
赛后修改为任意两点的最小步数，通过这道题了。

《完》

-EOF-

本文公众号：天空的代码世界
个人微信号：tiankonguse
公众号ID：tiankonguse-code