leetcode 第 418 场算法比赛

零、背景

这次比赛我有事没参加，最后看了下题目，发现最后一题比较难，但不知为啥第三题过得人比较少。

A: 枚举。
B: 图论搜索。
C: 图论找规律。
D: 枚举计算，前缀和。

排名：无
代码地址： https://github.com/tiankonguse/leetcode-solutions/tree/master/contest/4/418

一、连接二进制表示可形成的最大数值

题意：给几个数字，问转化为二进制后连接起来，可以得到的最大数字。

思路：枚举数字的所有排列组合，计算出二进制连接后的数字，求最大值。
复杂度：O(n! * n log(n))

二、移除可疑的方法

题意：给一个有向图，有一个节点是异常节点，异常节点可以到达的节点也是异常节点。
只有当一组节点没有被这组之外的任何节点调用时，这组节点才能被移除。
求最终没有被移除的节点列表。

思路：题目比较难理解。

异常节点可以通过 BFS 搜索得到。

根据题目定义，正常节点是不能删除的。
另外，不能删除的节点的所有子孙节点是不能被删除的。
最后，不能删除的节点的所有祖先也是不能删除的。

所以，我们需要维护两个队列，一个是子孙搜索队列，一个是祖先搜索队列。
最终计算出哪些节点不可以被删除。

优化：可以证明，只要存在一个正常节点可以到达任何一个异常节点，则所有异常节点都无法删除。
证明：有向图即求子孙，又求祖先，等价于无向图求联通分支。

故，只需要判断是否存在正常节点到异常节点的边，存在答案就是所有节点，否则就是所有正常节点。

三、构造符合图结构的二维矩阵

题意：给一个无向图，求图映射到矩阵里，使得图的顶点就是矩阵的坐标，边代表矩阵相邻节点。

思路：找规律。

分析矩阵的特征，可以发现图中顶点的度数存在规律。

规律1：1*N 的矩阵，两个顶点度数为1，其他顶点度数为 2。
规律2：M*N 的矩阵，4个顶点度数为2，边的顶点度数为3，中间顶点度数为 4。

针对规律1，可以直接找到一个顶点，边搜索边映射到矩阵。

针对规律2，需要先根据边度数为3的特征，找到一条边，之后，通过已找到的边就可以唯一确定相邻边。

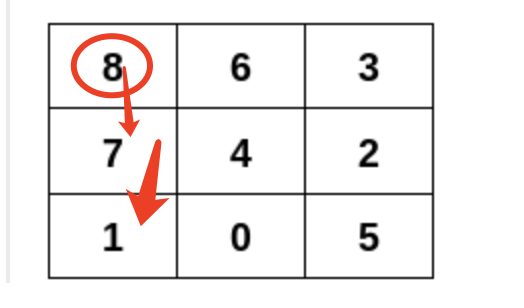
如下图，假设第一条边即第一列[8,7,1]已经找到并标记。
搜索顶点 8,只剩下顶点 6 未标记，所以顶点 6 需要放在顶点 8 的右边。
同理，顶点 4 需要放在顶点 7 的右边，顶点 0 需要放在顶点 1 的右边。
这样第二列的顶点就全部获取到。
按照同样的方法，循环获取矩阵所有列的顶点即可。

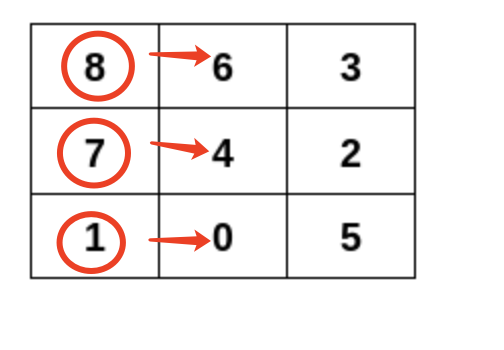
怎么获取第一列呢？
找到一个顶点后，随便选择一个相邻顶点，不断的搜索度数为 3 的顶点，直到搜到到度数为 2 的顶点结束。

不过需要对2*N 的矩阵做特殊处理，因为矩阵为 2*N的矩阵，搜索时，可以搜索到 2个度数为 3 的顶点。
特殊处理也很简单，随便找一个顶点，判断相邻的两个顶点是否存在度数为 2 的情况，存在了，就是 2*N的矩阵。

四、查询排序后的最大公约数

题意：给n个数字，两两组合求最大公约数，所有公约数排序，求第k个公约数。

思路：数学计算。

有 10^5个询问，每个询问必须在 log(n)的复杂度内计算出答案。
这就要求需要预先计算好答案。

逆向思考，n个数字最大值值为5*10^5，最大公约数也分布在 [1,5*10^5]内。
如果预先计算出每个最大公约数的组合个数，则可以通过前缀和，来快速找到第k个公约数的值。

map<ll, ll> sums; // 储存右边界
ll pre = 0;
for (int v = 1; v <= maxVal; v++) {
  if (gcdNums[v] == 0) continue;
  pre += gcdNums[v];
  sums[pre] = v;
}

for (auto q : queries) {
  ans.push_back(sums.lower_bound(q+1)->second);
}

怎么求出每个公约数的组合个数呢？
假设预处理出每个数字对应的约数，然后统计每个约数是几个数字的约数。
不妨设为 p 个，则可以推导出，这个约数的组合个数为 C(p,2)个。

vector<ll> gcdNums(maxVal + 1, 0);
for (ll v = 1; v <= maxVal; v++) {
    gcdNums[v] = factors[v] * (factors[v] - 1) / 2;
}

两个数字除了有最大公约数，还有很多其他公约数。
所以，上面的公式多计算了很多组合。
具体来说，除了最大公约数组合，其他公约数的组合都是无效的，都需要减去。

怎么求其他公约数呢？
枚举判断即可。

for (ll v = maxVal; v > 1; v--) {
  if (gcdNums[v] == 0) continue;
  // 有若干个数字，gcd() = v, 需要减去非最大公约数
  const ll sq = sqrt(v);
  for (ll a = 1; a <= sq; a++) {
    if (v % a != 0) continue;
    gcdNums[a] -= gcdNums[v];
    const ll b = v / a;
    if (a != b && b != v) {
      gcdNums[b] -= gcdNums[v];
    }
  }
}

复杂度：O(n sqrt(n))

五、最后

这次比赛所有题其实都挺有难度的。

第一题需要枚举所有排列。
第二题如果没发现规律，则需要维护子孙和祖先队列，或者维护一个无向图。
第三题先分析矩阵，会发现不难，我几分钟就想到过滤了。
第四题我感觉挺难的，我想了很多方法，比如二分、容斥，最后发现那些方法都行不通后，才一步步推导出行的通的方法。

总的来看，后三道题都挺有意思的，两个图论是找过滤，数学题则是思维题，想不到就很难通过了。

《完》

-EOF-

本文公众号：天空的代码世界
个人微信号：tiankonguse
公众号ID：tiankonguse-code