leetcode 第 427 场算法比赛

零、背景

这次比赛求坐标系最大矩阵，需要离散化+线段树+二分查找，相当复杂。

A: 模拟
B: 枚举
C: 分段最大子数组和
D: 离散化线段树+二分

排名： 200+
代码地址： https://github.com/tiankonguse/leetcode-solutions/tree/master/contest/4/427

一、转换数组

题意：给一个循环数组，求构造一个映射数组。
映射规则：如果元数组值是正数v，则取右边第v个位置的值，否则取左边第v个位置的值。

思路：按题意模拟即可。

优化：可以直接相加取模即可。

注意事项：负数可能是n的很多倍，取模后再加n，再取模即可。

for (int i = 0; i < n; i++) {
  ans[i] = nums[((i + nums[i]) % n + n) % n];
}

二、用点构造面积最大的矩形 I

题意：坐标系给n个点，求挑选4个点组成与坐标轴平行的面积最大的矩阵，且矩阵的内部和边界上没有其他点。

思路：枚举。

枚举 4 个点，再判断其他点是否在矩阵内或边界上。
复杂度：O(n^5)

优化：所有坐标优先 x轴其次y轴排序。

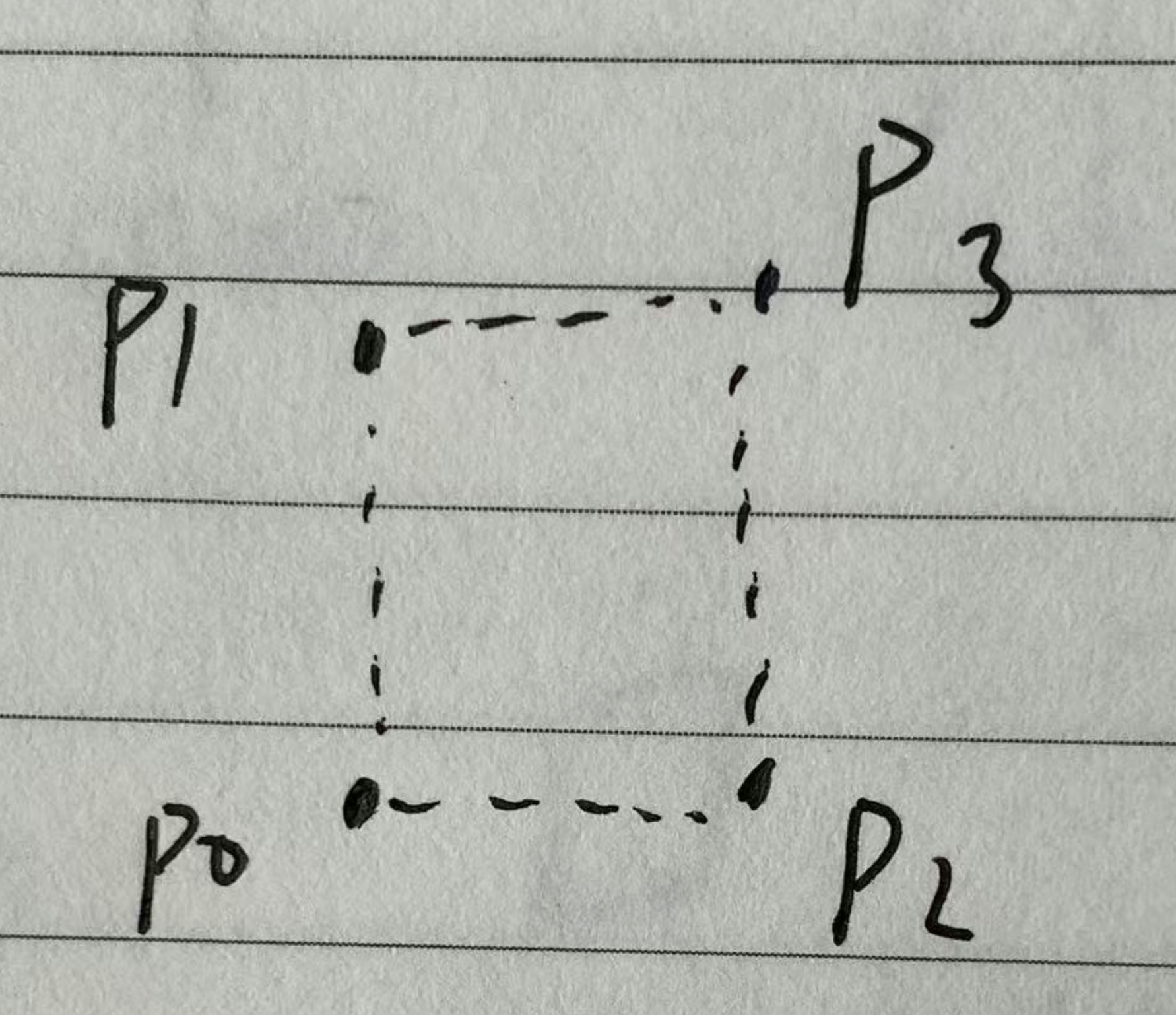
边界1：枚举第一个点后，下个点肯定是第二个点，且 x 轴相同。
边界2：第三个点肯定在 x 轴右边，且 y 轴与第一个点相等。
边界3：在找到第三个点之前，中间的点的 y 轴都不能在中间。
边界4：找到第三个点后，第四个点肯定是下个点，判断是否可以组成矩阵。

复杂度：O(n^2)

进一步优化见第四题。

三、长度可被 K 整除的子数组的最大元素和

题意：给一个个数组，问所有长度可以整除 k 的子数组的最大数组和。

思路：分段。

可以先划分出所有长度为 k 的子数组，相邻的长度为 k 的子数组之和就是长度为 2k 的子数组。

显然，可以根据起始位置，将长度为 k 的没有交集的子数组进行分组。
每组内连续的子数组可以组成 k 倍长度的子数组。
分组个数为 K，每组内线段个数为 n/k。

对于这样每个分组，我们需要找到一个连续的多个分段，使得分段和最大。
这个是典型的最大子数组和。
复杂度：O(K * n/K) = O(n)

for (int i = 1; i <= k; i++) {
  ll pre = 0;
  for (int j = i; j <= n; j += k) {
    int l = j;
    int r = j + k - 1;
    if (r <= n) {
      ll now = preSum[r] - preSum[l - 1];
      pre += now;
      Update(pre);
      if (pre < 0) {
        pre = 0;
      }
    }
  }
}

四、用点构造面积最大的矩形 II

题意：坐标系给n个点，求挑选4个点组成与坐标轴平行的面积最大的矩阵，且矩阵的内部和边界上没有其他点。

思路：与第二题一摸一样，数据范围变大了。
第二题已经优化到O(n)，这里需要继续优化。

先回头看下第二题的优化。

优化：所有坐标优先 x轴其次y轴排序。
边界1：枚举第一个点后，下个点肯定是第二个点，且 x 轴相同。
边界2：第三个点肯定在 x 轴右边，且 y 轴与第一个点相等。
边界3：在找到第三个点之前，中间的点的 y 轴都不能在中间。
边界4：找到第三个点后，第四个点肯定是下个点，判断是否可以组成矩阵。

复杂度分析：
寻找第二个点：第一个点的下一个就是第二个点，复杂度O(1)。
寻找第三个点：需要跳过边界外的点，寻找边界内x轴最小的时最小的y，复杂度O(n)
寻找第四个点：第三个点的下一个点就是第四个点，复杂度O(1)

可以发现，关键在于确定前两个点后，无法快速找到第三个点，所以只能一个个枚举判断，导致复杂度较低。

p0 对应 X 轴右边的所有点如果都储存在线段树里，则查询区间[P0_y, P1_y]的最小坐标就是第三个点。

问题：X 轴的点枚举完了，如何从线段树中删除 X 轴的点。
方法：所有点按 X 轴分组，即每个 X轴对应一个数组，相同 X 轴的点放在数组里。

问题：Y 轴相同时，线段树里只能储存 X 轴最小的那个点。
方法：删除一个点后，把相同 Y 轴的右边的第一个点加入进来。

问题：删除一个点时，怎么找到相同 Y 轴右边的第一个点。
方法：所有点按 Y 轴分组，分组内按 X 轴排序，即可二分查找得到。

小技巧：所有点按 X 轴与 Y 轴分组后，第一个点找第二个点，以及第三个点找第四个点，都可以二分查找得分。

离散化代码：

vector<ll> yh = {yCoord.begin(), yCoord.end()};
sort(yh.begin(), yh.end());
yh.erase(unique(yh.begin(), yh.end()), yh.end());

const int yn = yh.size();
unordered_map<ll, ll> YH;
for (int i = 0; i < yn; i++) {
  YH[yh[i]] = i;
}

分组代码：

vector<vector<ll>> Yarray(yn);
for (int i = 0; i < n; i++) {
  auto [x, y] = points[i];
  Yarray[YH[y]].push_back(XH[x]);
}
for (int i = 0; i < yn; i++) {
  sort(Yarray[i].begin(), Yarray[i].end());
}

删除 X 轴的所有点代码

if (X0 != preX) {
  // 处理到新的第 X 列，X 列的所有 Y 肯定在线段树里， 更新线段树
  for (ll XY : Xarray[X0]) {
    auto it = upper_bound(Yarray[XY].begin(), Yarray[XY].end(), X0);
    Point p = {INT_MAX, INT_MAX};
    if (it != Yarray[XY].end()) {
      p = {*it, XY}; // Y 轴下个点
    }
    segTree.Update(XY + 1, p);
  }
  preX = X0;
}

查找三个点，计算答案：

// 查找 X1
auto it1 = upper_bound(Xarray[X0].begin(), Xarray[X0].end(), Y0);
if (it1 == Xarray[X0].end()) {
  continue;  // 同一列没有下一个
}
const auto [X1, Y1] = Point{X0, *it1};

// 根据大小顺序关系，区间最小值肯定是右下角坐标
auto [X2, Y2] = segTree.QueryMin(Y0 + 1, Y1 + 1);
if (X2 == INT_MAX || Y2 != Y0) {
  continue;  // 右边没有点了
}

auto it3 = upper_bound(Xarray[X2].begin(), Xarray[X2].end(), Y2);
if (it3 == Xarray[X2].end() || *it3 != Y1) {
  continue;  // 同一列没有下一个
}
const auto [X3, Y3] = Point{X2, *it3};

ans = max(ans, (xh[X3] - xh[X1]) * (yh[Y1] - yh[Y0]));

五、最后

这次比赛第四题其实不难吗，但是离散化 + 线段树 + 各种二分，代码量很是很大的，相当于一个大的模拟题了。

《完》

-EOF-

本文公众号：天空的代码世界
个人微信号： tiankonguse
公众号ID： tiankonguse-code