leetcode 第 432 场算法比赛，翻车了

背景

这次比赛第三题没想明白，直接做第四题，结果使用滑动窗口实现，是个大模拟，比赛结束才敲出来。

A: 模拟
B: 动态规划
C: 二分+DFS
D: 滑动窗口、线段树、ST表、二分

排名：200以后
代码地址： https://github.com/tiankonguse/leetcode-solutions/tree/master/contest

一、跳过交替单元格的之字形遍历

题意：给一个矩阵，从上到下扫描，奇数行从左到右，偶数行从右到左，问路径上奇数位置值组成的数组。

思路：按题意模拟即可。

二、机器人可以获得的最大金币数

题意：给一个矩阵，只能向右走与向下走，问从左上角到右下角，最大路径和。
魔法：有两次机会忽略路径上某个点的值。

思路：动态规划。

状态定义：f(x,y,k) 使用 k 次魔法到达 (x,y) 的最大路径和。
状态转移：

// 不使用魔法
dp[i][j][k] = max(dp[i][j][k], dp[i - 1][j][k] + v);
dp[i][j][k] = max(dp[i][j][k], dp[i][j - 1][k] + v);

// 使用魔法
dp[i][j][k] = max(dp[i][j][k], dp[i - 1][j][k - 1]);
dp[i][j][k] = max(dp[i][j][k], dp[i][j - 1][k - 1]);

三、图的最大边权的最小值

题意：给一个有向图，问删除一些边后，是否可以组成下面条件的图。

条件1：所有其他节点都可以到达节点 0 。
条件2：图中剩余边的 最大 边权值尽可能小。
条件3：每个节点都 至多 有 threshold 条出去的边。

求满足条件时，最大边权的 最小值 为多少。

思路：题目的有向边是反向的，有很大的干扰性。

第一步是反向建图，则条件变为：

条件1：节点 0 可以到达所有顶点 。
条件2：图中剩余边的 最大 边权值尽可能小。
条件3：每个节点都 至多 有 threshold 条进去的边。

接下来分析一下三个条件。

条件1要求是联通图，最优解肯定是一个树。
条件3要求至多有 threshold 个入度边，树都有1 个入度边，所以都满足要求。
条件2 要求边尽可能小，方法很多。

比赛时，条件3没想清楚，于是放弃这道题了。

方法1：二分答案，判断小于等于二分值的边是否联通。
复杂度：O(n log(n))

方法2：并查集。
边数从小到大合并，当合并到一个联通时，最后一条边就是答案。

方法3：搜索

错误的贪心：有人会贪心储存入度的边权，当有更小的边权时，重新搜索，这样存在反例。
例如根到其他节点的边权都很大，其他节点互相连接，边权很小，贪心时其他节点的边权就都会被更新，从而得到错误的答案。

正确的搜索应该是未搜索节点才能更新边权，搜索过后，不能更新边权。

四、统计 K 次操作以内得到非递减子数组的数目

题意：给一个数组，问存在多少个子数组，通过最小修改 k 次使得子数组是非递减的。
修改：每次选择一个元素加1。

思路1： 滑动窗口，枚举左边界大模拟

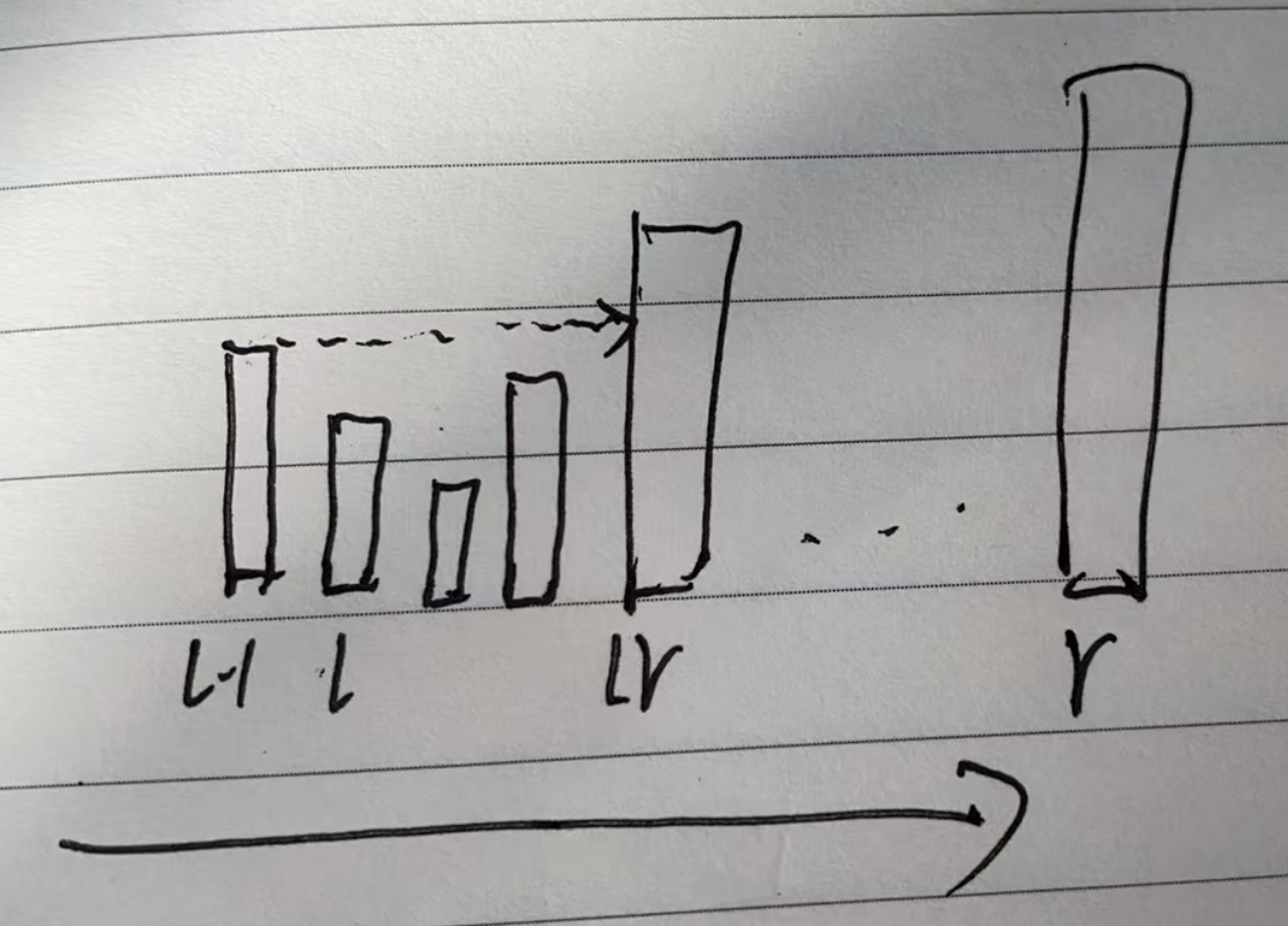
假设前一个位置已经计算出最多修改 k 次时的最大区间 [l-1, r]。
当前位置分为两种情况：

情况1：nums[l] >= nums[l-1]
此时可以完美复用上一个区间的答案，因为 k 次修改只能使区间 [l,r] 满足要求，再多一个就无法满足了。

情况2：nums[l] < nums[l-1]
假设大于等于 l-1 的位置为 lr，则显然， [l, lr-1] 区间内的元素值都小于 nums[l-1]。
进一步可以确定，在 l-1为边界时，``[l, lr-1] 的值都向上补齐到了 nums[l-1]`。

左边界降低为 nums[l]后，区间[l, lr-1] 的元素需要重新计算。
故在边界 l-1 进行的修改，在l 都需要补偿回来，补偿值为 nums[l-1]*(lr-l) - sum[l,lr-1]。

之后，需要计算区间 [l, lr-1] 做到非递减的最小操作数。
正常思路是循环遍历，复杂度是 O(n)。
如果我们预处理出每个位置右边第一个大于等于的位置，显然，区间内的都需要补充对齐，故可以通过区间和求差快速补齐。
可以证明，整个滑动窗口期间，每个位置只进行一次这样的计算，故累计复杂度为O(n)。

特殊情况：l-1的值可能很大，此时区间[l,r]的值可能都比较小。
此时，区间需要修正为 [l, min(lr-1, r)]，计算完之后，r 需要继续向右循环探测。
最优解时二分向右探测，但其实可以直接不断加1探测，累计复杂度依旧是 O(n)

思路2：逆向滑动窗口，枚举左边界

参考代码：第四名 Hack_Others 我比赛的时候之所以把滑动窗口写的很复杂，是因为是正向处理的。
如果我们来逆向处理，就会发现不存在各种特殊边界，只需要出栈与入栈即可。
复杂度：O(n)

思路3：正向滑动窗口，枚举右边界
参考代码：第三名 TsReaper
与逆向滑动窗口，枚举左边界类似，从右到左了，枚举左边界，从左到右了，枚举右边界，都会简单很多。

思路4：二分套二分
参考代码：第一名 小咩肖恩
从大到小枚举左边界，二分右边界需要的修改是否不大于K。
左右边界确定后,如何求修改数呢？

需要动态维护一个单调栈。
单调栈相邻元素满足下个元素是当前元素右边第一个大于等于的元素。

如下图，维护一个单调栈以及单调栈的后缀和。
则可以再次二分后缀和，找到完整的区间，与最后部分区间，从而计算出总修改数。

复杂度：O(n log(n) log(n))

思路5：ST 表。

参考代码：第二名，红与黑
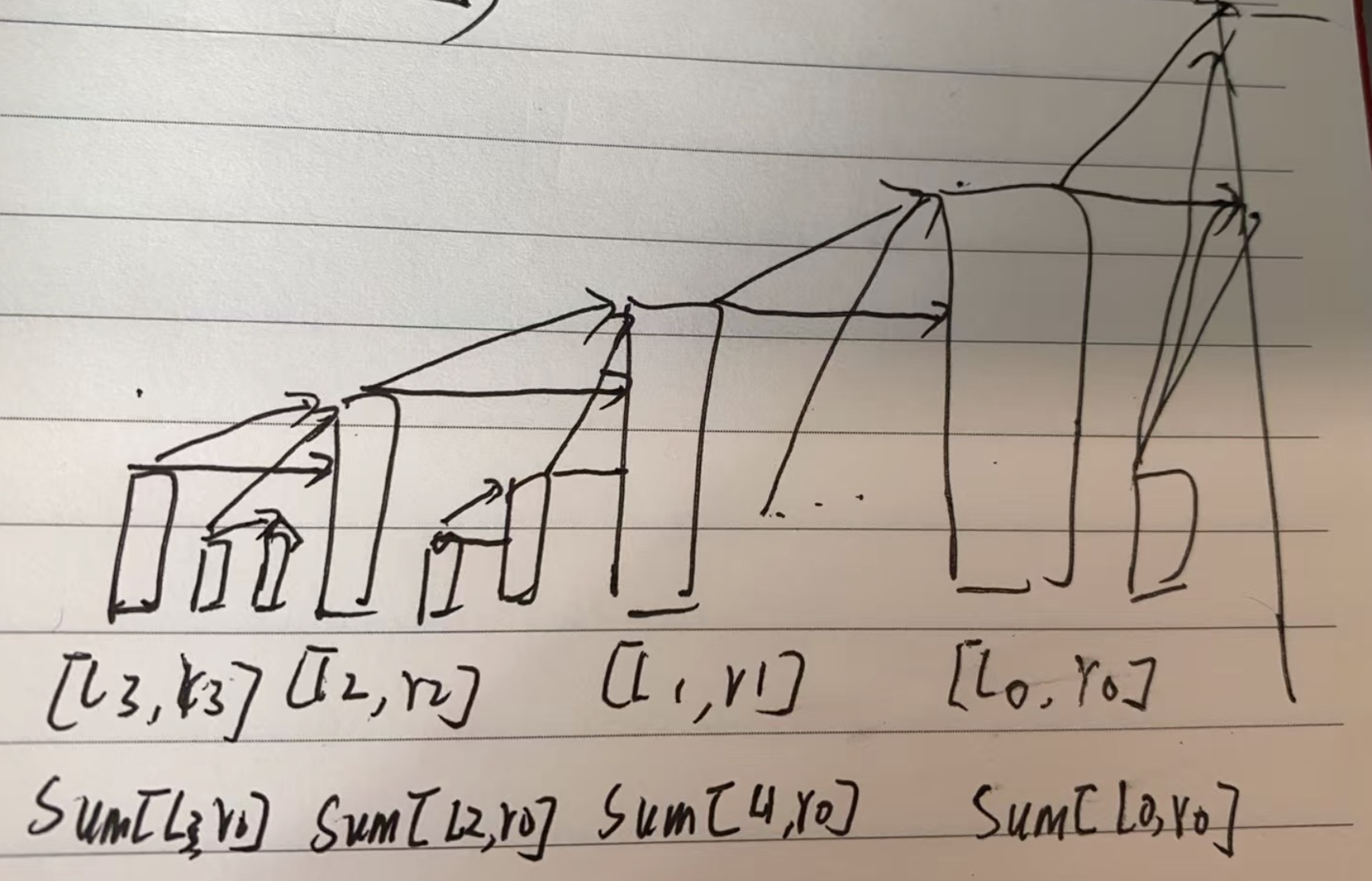
还是计算出每个元素右边第一个不大于的位置，可以画出关系图，是不是很像树状数组。
其实这个关系，从后到前看，就是一个有根树。
有根树求区间，可以使用 ST 表来快速确定边界的。

五、最后

这次比赛第三题卡主了，直接跳过没做。
第四题做复杂了，变成一个很大的模拟题，代码量很大。

第三题的经验是，读题还是需要认真，逐个条件与要求去转换，避免遗漏。
第四题的经验是，当发现代码量很大时，要及时停止，去思考是否方向错了，否则就是很大的模拟题。

《完》

-EOF-

本文公众号：天空的代码世界
个人微信号： tiankonguse
公众号ID： tiankonguse-code