leetcode 第 436 场算法比赛

背景

我多年来一直在坚持参加 leetcode 周赛，并发布题解。
现在整理了一个leetcode 周赛题解大全。
地址为：https://mp.weixin.qq.com/s/64TblIROBAfZNim89kylHw

春节后一周我请了几天假，周日还在路上，所以没有参加比赛。
现在趁着周末，把比赛补一下。

A: 模拟
B: 筛法
C: DP
D: 二分

排名：未参加比赛
代码地址： https://github.com/tiankonguse/leetcode-solutions/tree/master/contest

一、按对角线进行矩阵排序

题意：给一个矩阵，按斜线排序，左下部分降序，右上部分升序。

思路：按题意扫描所有斜线，按要求升序或降序排序，然后按扫描规则填充回矩阵。

二、将元素分配给有约束条件的组

题意：给两个数组 A 和 B，问对于 A 的每个元素，求 B 中第一个可以整除的下标，如果不存在返回 -1。
数组大小：10^5
值范围：10^5

思路：筛法。

对 B 数组求筛法，计算出 10^5 范围内所有值的答案，然后填充 A 数组的答案即可。
小技巧：只需要对 A 数组最大值范围内的数据进行筛法即可。

vector<int> G(maxVal + 1, N);
int en = elements.size();
for (int i = 0; i < en; i++) {
  int v = elements[i];
  if(v > maxVal) continue;
  if (G[v] != N) continue;
  for (int j = v; j <= maxVal; j += v) {
    G[j] = min(G[j], i);
  }
}

三、统计可以被最后一个数位整除的子字符串数目

题意：给一个数字字符串，问所有子串中，有多少子串可以整除子串的个位数字。

思路：枚举+DP

数字只有10个，0 不可能有答案，枚举1到9。
此时问题转化为了：有多少子串个位为 x 且取模 x 后为 0。

我们可以通过 DP 计算出取模 x 为所有值的个数。

状态定义：nums[i][k] 以第i个位置为个位的所有子串取模 x 值为 k 的个数。
状态转移方程如下：

// v 第 i+1 位的值
nums[i+1][v % p]++; 
nums[i+1][(k * 10 + v) % p] += nums[i+1][k];

四、最大化游戏分数的最小值

题意：给一个一维坐标轴各位置的单位分数，起始在坐标-1，可以左移与右移，进入某个坐标，坐标就加上单位分数。
问最多移动 m 次，问如何移动，才能使得所有坐标里的最小值最大。

思路：最小值最大，二分。

具体来说，是二分答案，判断满足答案至少需要移动多少次。

ll l = 0, r = V * m;  // 只有2个，来回跑，最大值为 V*(m+1)/2
while (l < r) {       // [l, r)
  ll mid = (l + r) / 2;
  if (Check(mid)) {
    l = mid + 1;
  } else {
    r = mid;
  }
}
return r - 1;

最小值确定后，可以计算出坐标轴每个点最少到达的次数。

for (int i = 0; i < n; i++) {
  ll v = points[i];
  nums[i] = (minVal + v - 1) / v;  // 至少需要到达多少次，才能不小于最小值
  sum += nums[i];
  if (sum > m) return false;
}

另外分析移动路线，可以发现多个节点的来回移动与两个节点间来回移动是等价的。

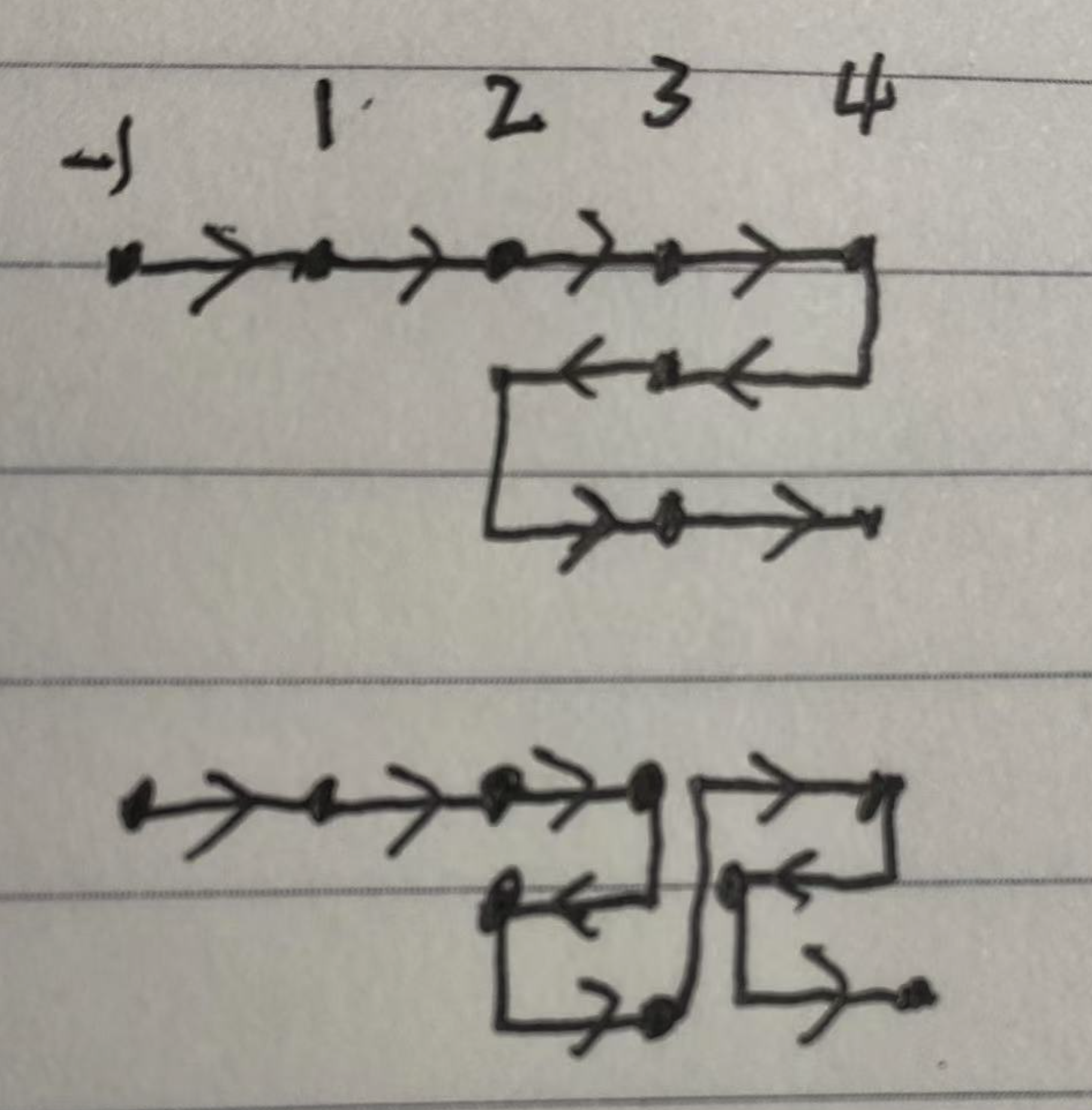
如果结束位置在最后一个节点，当前节点到达 a 次，则下个节点至少需要为 a 次才能来回移动，如果不够，就需要额外补充至 a 次。
来回移动后，记录下个节点占用的次数，从而可以计算出剩余的次数。

// 优先贪心计算，在 n-1 结束，需要多少次操作
for (int i = 0; i < n; i++) {
  if (i + 1 < n) {  // 不是最后一个, 前面与下一个来回移动
    ll now = adds[i] + nums[i];
    ll left = now - uses[i];
    if (left > nums[i + 1]) {
      adds[i + 1] += left - nums[i + 1];
      addNum += left - nums[i + 1];
    }
    uses[i + 1] += left - 1;  // 来回移动
  } else {                   
     // 最后一位
  }
}

对于最后一位，如果有剩余的，需要与前一位来回移动。

if (i + 1 < n) {
  // 不是最后一个, 前面与下一个来回移动
} else {                    // 最后一位
  ll now = adds[i] + nums[i];
  ll left = now - uses[i];
  if (left > 1) {  // 与左边的来回移动
    adds[i - 1] += left - 1;
    addNum += left - 1;
  }
}

结束位置并没有要求一定要在最后，所以对于额外增加的次数，可以反悔贪心。

for (int i = n - 1; i > 0; i--) {
  if (adds[i] > 0) {
    adds[i]--;
    addNum--;
  } else {
    break;
  }
}

最后判断个数是否大于 m。

return sum + addNum <= m;

五、最后

这个比赛最后一题二分后的构造挺不好想的，需要先贪心构造到最后的答案，然后返回贪心，构造出正确的答案。

《完》

-EOF-

本文公众号：天空的代码世界
个人微信号： tiankonguse
公众号ID： tiankonguse-code

本文首发于公众号：天空的代码世界，微信号：tiankonguse
如果你想留言，可以在微信里面关注公众号进行留言。