leetcode 第 438 场算法比赛

背景

2025 年 leetcode 比赛越来越难了。
第三题竟然是非质数的乘法逆元，第一次遇到，触发我的知识盲区了。

我的猜测是：leetcode 原先是面向公司招聘的，如今行业不景气，leetcode 从招聘上的收入越来越少了。
所以 leetcode 打算转型，面向中学的算法比赛，以后依靠会员来提高收入，由此提高了算法难度。

A: 模拟
B: 堆或排序
C: 组合数学与乘法逆元
D: 二分贪心

排名：200+
代码地址： https://github.com/tiankonguse/leetcode-solutions/tree/master/contest

一、判断操作后字符串中的数字是否相等 I

题意：给一个整数数组，每次相邻整数相加由此得到新的长度减一的数组，不断重复操作，直到数组长度为二，问此时剩余的两个元素的个位是否相等。

思路：模拟

按题意不断模拟操作，每次数组长度减一，减到剩余两个元素时，判断个位是否相等即可。

二、提取至多 K 个元素的最大总和

题意：给一个矩阵，每一行有个可以选择数字的数量限制，现在共需要选择 k 个数组，问怎么选择才能使得选择的数字和最大。

思路：堆或排序

方法1：排序+堆

对每一行从大到小排序，然后把这一行数量限制之内的数字加入大小最多为K的小顶堆中。
小顶堆数量超过 K 时，就把最小元素删除。
最后堆中的元素求和即可。

复杂度：O(n * m * (log(m) + log(k))))

方法2：排序。

矩阵转化为一维数组，元素值是 {val, rowIndex}，之后逆序排序。
从大到小加入元素，并统计每一行已经加入的个数，到达限制时这一行就不再加入。
复杂度：O(n*m*log(n*m))

三、判断操作后字符串中的数字是否相等 II

题意：给一个整数数组，每次相邻整数相加由此得到新的长度减一的数组，不断重复操作，直到数组长度为二，问此时剩余的两个元素的个位是否相等。

思路：组合数学与乘法逆元

由于下一行的元素是上一行相邻两个数组的和，很容易发现，最终的答案是原始数组各元素乘以系数后的和。
第一个数字对应的元素区间是 [0, n-2]，第二个数字对应的元素区间是 [1,n-1]。
各系数对应组合数 C(n-2, i)。
所以问题转化为了 sum(ai * C(n-2, i)) % 10

在计算这个公式之前，需要先了解几个基础知识。

1）乘法逆元
如果 gcd(a,b)=1 且 x/a 可以整除，则x/a%p 等价与 x * a^-1 % p。
其中 a^-1 是 a 关于 p 的逆元。

这道题 p 为 0，不满足情况，所以我们需要做一下因式分解，使得除法满足乘法逆元。
推导公示如下

有了上面的公式，我们就可以预处理出所有剔除掉2和5的阶乘与阶乘逆元，然后套公式即可。

阶乘的预处理伪代码如下：

A[0] = 1;
for (int i = 1; i <= n; i++) {
  ll x = i;
  int x2 = 0, x5 = 0;
  while (x % 2 == 0) {
    x2++;
    x /= 2;
  }
  while (x % 5 == 0) {
    x5++;
    x /= 5;
  }
  A[i] = (A[i - 1] * x) % mod;
  A2[i] = A2[i - 1] + x2;
  A5[i] = A5[i - 1] + x5;
}

阶乘逆元的伪代码如下：

阶乘逆元也可以递推计算， 由于 n! = n * (n-1)!， 因此可以推导出 inv(n-1）= n * inv(n)。
利用这个推导公式，我们就可以从后到前推导出所有阶乘逆元。

RA.resize(n + 1);
RA[n] = inv(A[n], mod);
for (int i = n; i > 0; i--) {
  ll x = i;
  int x2 = 0, x5 = 0;
  while (x % 2 == 0) {
    x2++;
    x /= 2;
  }
  while (x % 5 == 0) {
    x5++;
    x /= 5;
  }
  RA[i - 1] = RA[i] * x % mod;
}

四、正方形上的点之间的最大距离

题意：给一个正方形，问正方形边长上选择 k 个点，任意两点之间最短距离的最大值是多少。

思路：最小的最大，二分。

二分后，问题转化为了是否存在 k 个点，使得任意两点的距离都不小于 mid。

ll l = 1, r = side + 1;
while (l < r) {
  ll mid = (l + r) / 2;
  if (checkAll(mid)) {
    l = mid + 1;
  } else {
    r = mid;
  }
}
return r - 1;

由于点都在正方向上，很容易发现同一个边上的点可以二分查找。
相邻边上的点，也可以二分查找。
而对面边上的点，就不满足二分了。

另外，由于某条边上可能没点，我们需要判断下个点属于哪种情况，这样做的话，就需要写 4*4=16 中 if/else 与二分查找，代码非常复杂。

还好，题目说 k 至少为 4。
如果 k 大于 4 时，根据容斥原理，最短距离不会超过边长。
可以证明，k 等于 4 时，最短距离也不会超过边长。

有了这个结论，边对面的点就一定满足要求了。

我们可以把四条边的坐标顺时针转化为一维坐标，之后可以枚举起始位置，然后去贪心二分查找 k 个点。

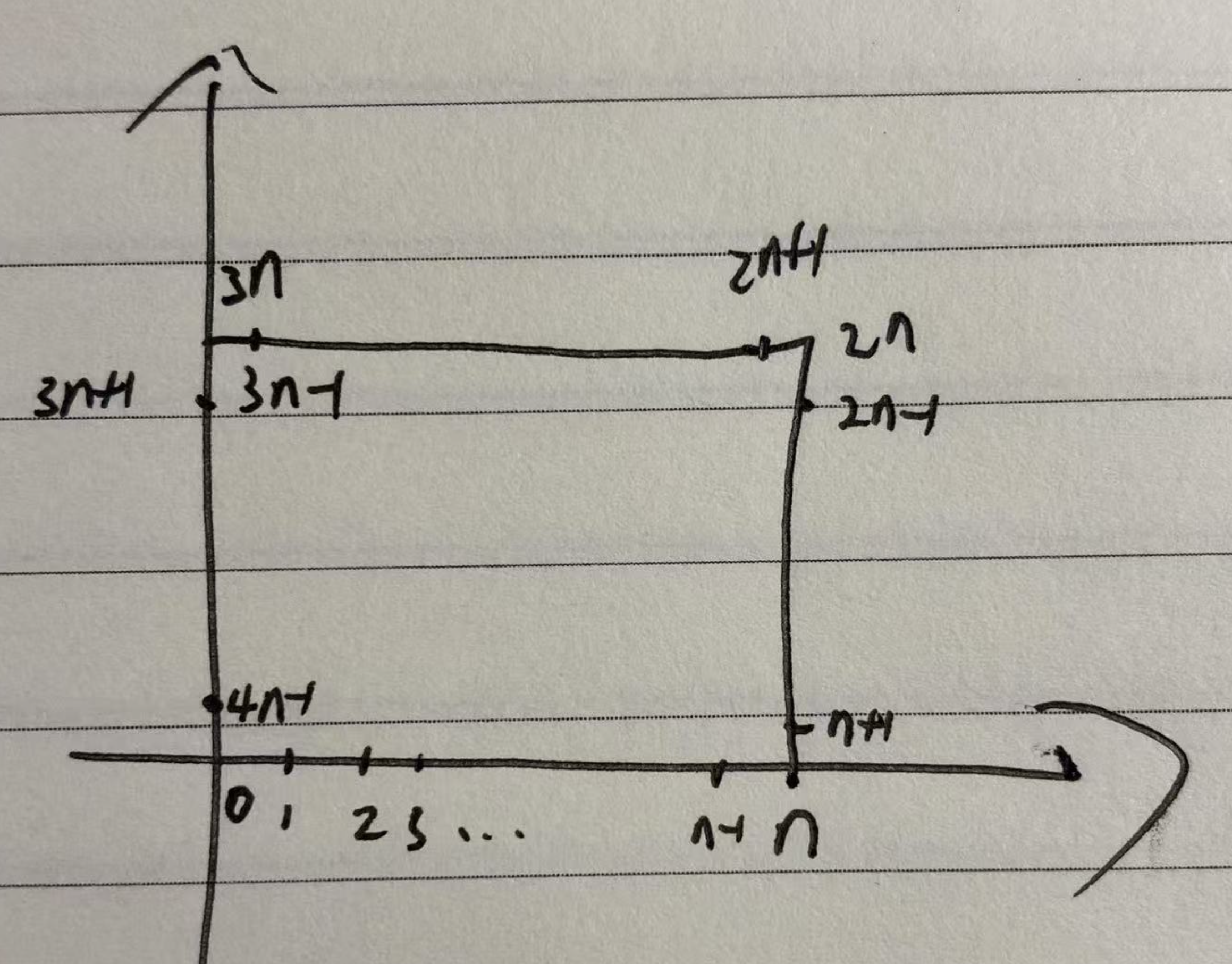
如果枚举的位置在后面了，就需要转回到前面，为了避免处理环，我们可以把整个一维数组再复制一遍。

等着，假设枚举的是第一个点，如果找到最后一个点，最后一个点与第一个点可能不满足答案。
所以我们找到 k 个点后，需要判断最后一个点与第一个点是否满足条件即可。

auto checkOne = [n, side, k, &rows](const int p, const ll mid) -> bool {
  int num = 1;
  const ll firstVal = rows[p];
  ll preVal = firstVal;
  int offset = p;
  while (num < k) {
    auto it = lower_bound(rows.begin() + offset + 1, rows.end(), preVal + mid);
    if (it == rows.end()) return false;
    offset = it - rows.begin();
    if (p + n <= offset) return false; // 剪枝，转了一圈了，没答案
    preVal = *it;
    num++;
  }
  if (firstVal + 4 * side - preVal < mid) { //首位判断
    return false;
  }
  return true;
};

另外，枚举的时候，也有两个剪枝策略。

1）假设有答案，则答案肯定会尽量平均的分布在四个边上，所以我们只需要枚举一个边即可。
2）四条边要分k分，想要间隔最大，就要分配的尽量平均，间隔上限是周长分k分。

// 优化前 172ms
auto checkAll = [side, k, n, &rows, &checkOne](const ll mid) -> bool {
  // 优化1 容器原理， 4*side 的位置，分成 k 分，间隔至少为 (4*side - k) / (k - 1)
  if (1 + mid * (k - 1) > 4 * side) return false;  // 142ms
  // 第一个点肯定在第一个边上
  const ll firstVal = rows[0];
  for (int i = 0; i < n; i++) {
    if (rows[i] - firstVal > side) return false;  // 剪枝，只需要枚举一个边，63ms
    if (checkOne(i, mid)) {
      return true;
    }
  }
  return false;
};

优化前复杂度：O(log(S) * n * k * log(n))
优化后复杂度：O(log(S) * n * log(n))

可以发现，优化后，把 k 优化没了，所以 k 即使很大，我们这个算法也不会超时。

大家可以思考下，如果 k 是 2 或者 3 时，有什么简单的方法来做呢？

五、最后

这次比赛第三题非常难，之前没做过，我是不会做。
第四题不好想，我推导出答案不超过边长，所以最终没做出来。

第一次只做出两道题，过年后真的变菜了。

《完》

-EOF-

本文公众号：天空的代码世界
个人微信号： tiankonguse
公众号ID： tiankonguse-code