leetcode 第 449 场算法比赛

零、背景

这次比赛最后一题的边界一直没还清楚，最后差一秒才通过。

A: 统计
B: 前缀和
C: 贪心
D: 前缀和+二分

排名：200+
代码地址： https://github.com/tiankonguse/leetcode-solutions/tree/master/contest

一、不同字符数量最多为 K 时的最少删除数

题意：给一个字符串，问最少删除多少个字符，才能使得剩余的不同字符个数最多为 K。

思路：统计。

保留的 K 个不同字符，一个都不能删除，其余的都需要删除。
显然，需要优先删除出现次数较少的字符。

算法：统计字符的频次，排序，保留频次最高的 K 个字符，其余字符都需要删除。

二、等和矩阵分割 I

题意：给一个矩阵，问是否可以水平或垂直拆分为两个矩阵，使得两个矩阵的和相等。

思路：前缀和。

预处理出每一行的前缀和与每一列的前缀和，然后枚举行与列的分割线，判断两个子矩阵和是否相等即可。

for (int i = 0; i < n; ++i) {
  for (int j = 0; j < m; ++j) {
    row[i] += grid[i][j];
    col[j] += grid[i][j];
    sum += grid[i][j];
  }
}
for (int i = 1; i < n; ++i) {
  if (sum % 2 == 0 && row[i - 1] == sum / 2) return true;
  row[i] += row[i - 1];
}
for (int j = 1; j < m; ++j) {
  if (sum % 2 == 0 && col[j - 1] == sum / 2) return true;
  col[j] += col[j - 1];
}

三、图中边值的最大和

题意：给一个无向图，每个节点最多与其他两个节点相连。
现在需要给图中节点分配权值，边的权值是两个节点权值之积，求所有边的权值之和的最大值。

思路：贪心。

每个节点最多连接两个节点，所以每个联通分支要么是一个环，要么是一个链。

之后就是贪心了。

假设只有一个环，则参考样例2，先填最大值，左右一次填写数字。

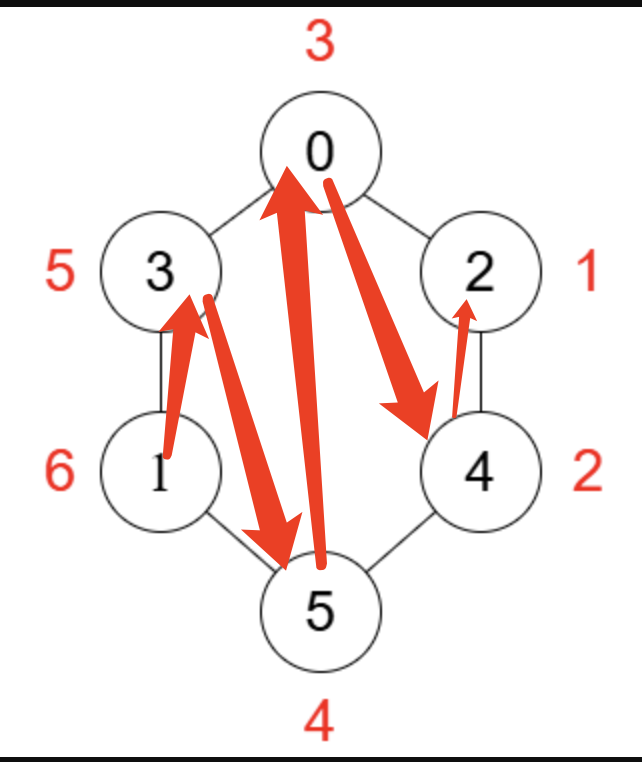
假设只有一个链，与环类似，参考样例1，在中间填最大值，然后最优依次填写数字。

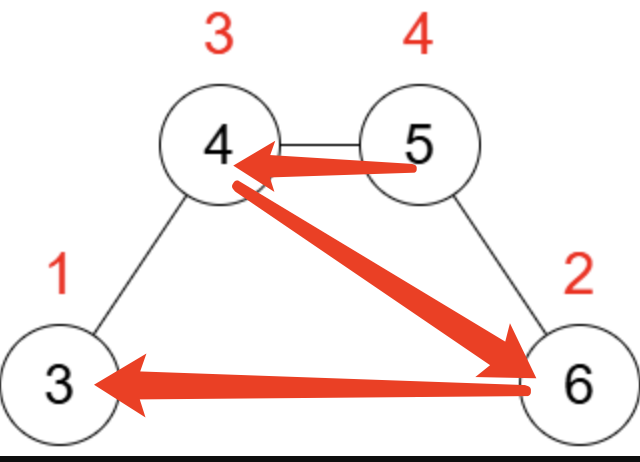
假设有一个环和一个链，参考样例1，可以猜测优先选择环，答案更优。

假设有多个环，可以猜测，先选择节点更多的环答案更优。

假设有多个链，可以猜测，先选择节点更多的链答案更优。

综合就是，优先选择环，然后选择链。
不断对于环还是链，由于选择多的，再选择少的。

首先使用并查集，计算出所有环和链，以及对应的节点个数。

Dsu dsu;
dsu.Init(n);
unordered_set<int> loop;
for (auto& edge : edges) {
  int u = dsu.Find(edge[0]);
  int v = dsu.Find(edge[1]);
  if (u == v) {
    loop.insert(u);
  } else {
    dsu.Union(u, v);
  }
}
vector<ll> links;
vector<ll> loops;
for (int i = 0; i < n; i++) {
  int f = dsu.Find(i);
  if (i == f) {
    if (loop.count(f)) {
      loops.push_back(dsu.GetScore(f));
    } else {
      links.push_back(dsu.GetScore(f));
    }
  }
}

然后按照上面的结论进行贪心。

sort(links.begin(), links.end(), greater<ll>());
sort(loops.begin(), loops.end(), greater<ll>());
ll ans = 0;
ll index = n;
enum { LINK = 0, LOOP = 1 };
auto Next = [&](int v, int type) {
  ll l = index--;
  ll r = l;
  v--;
  while (v >= 2) {
    ll L = index--;
    ll R = index--;
    ans += l * L;
    ans += r * R;
    l = L;
    r = R;
    v -= 2;
  }
  if (v == 1) {
    ll L = index--;
    ll R = L;
    ans += l * L;
    if (type == LOOP) {
      ans += r * R;
    }
  } else {
    if (type == LOOP) {
      ans += l * r;
    }
  }
};
for (ll v : loops) {  // 长度为 v 的环
  Next(v, LOOP);
}
for (ll v : links) {  // 长度为 v 的链
  Next(v, LINK);
}
return ans;

四、等和矩阵分割 II

题意：与第二题，这里允许最多删除一个坐标，但是修改后两个子矩阵的剩余元素需要是连续的。

思路：前缀和与二分。

不修改的情况与第二题一模一样，可以直接使用第二题的代码。
之后枚举删除所有坐标，判断删除后，是否存在拆分，使得子矩阵和相等，子矩阵还联通。

以行为例，假设删除的是 (x,y)，分割线可能在 x 的上边，也可能在 x 的下边。

如果分割线在 x 的上边，则说明分割线之前的前缀和都不变，直接二分查找即可。

特殊情况：找到后，由于是下半部进行删除，下半部可能不联通。
这里分三种情况讨论：

1）如果行和列都大于2，则删除肯定联调。
2）如果只有一列，删除点只能在两边，不能在中间。
3）如果只有一行，删除点只能在两边，不能在中间。

// 分割线 limit 在 x 之前 [0, x)，即前缀和不需要减去 v，此时 row[limit] == target
if (x - 1 >= 0 && row[x - 1] >= target) {  // 肯定可以查找到
  auto limit = lower_bound(row.begin(), row.end() + x, target) - row.begin();
  if (row[limit] == target) {
    if (m >= 2 && n - limit > 2) return true;                   // 至少两行两列中删除，必然联通
    if (m == 1 && (limit + 1 == x || x + 1 == n)) return true;  // 只有一列，删除的元素在分割线的两侧
    if (n - limit == 2 && (y == 0 || y + 1 == m)) return true;  // 只有一行，删除的元素在分割线的两侧
  }
}

如果分割线在 x 的下边，下标的都需要减去 v，此时需要查找 row[limit] == target - v。

如下代码，查找到目标值后，需要判断是否联通。
判断方法与上面类似，这里不再赘述。

// 分割线 limit 在 x 之后 [x, n)，则需要 row[limit] - v == target
if (x < n - 1 && row[x] - v <= target) {
  auto limit = lower_bound(row.begin() + x, row.end(), target + v) - row.begin();
  if (row[limit] == target + v) {
    if (m >= 2 && limit + 1 >= 2) return true;              // 至少两行两列中删除，必然联通
    if (m == 1 && (x == 0 || x + 1 == limit)) return true;              // 只有一列，删除的元素在分割线的两侧
    if (limit == 0 && (y == 0 || y + 1 == m)) return true;  // 只有一行，删除的元素在分割线的两侧
  }
}

五、最后

这次比赛第三题需要大胆的贪心，第四题边界处理比较麻烦，我没处理好，结束比赛后的一秒才通过。

《完》

-EOF-

本文公众号：天空的代码世界
个人微信号： tiankonguse
公众号 ID： tiankonguse-code

本文首发于公众号：天空的代码世界，微信号：tiankonguse
如果你想留言，可以在微信里面关注公众号进行留言。

leetcode 第 449 场算法比赛 - 贪心模拟