leetcode 第 451 场算法比赛-差点第20名

零、背景

这次比赛后两题都会做，评估代码量后，我觉得最后一题更简单一些。
结果敲完后 leetcode 运行不能看到结果，于是搭建本地编译测试环境，浪费不少时间。

不过提交后，有一组 case 没过，修改后再次提交后就过了，不过已经比赛结束 7 分钟了。
查看榜单，如果最后一题通过的话，排名第 20 名。

A: 数学计算
B: 栈
C: 树形DP+普通DP
D: 枚举DP

排名：200+
代码地址： https://github.com/tiankonguse/leetcode-solutions/tree/master/contest

一、木材运输的最小成本

题意：给一根长度为 n 的木头，一次最多承载长度为 k 的木头，所以需要对木头进行分割，求最小分割代价。
分割代价：一个木头切割为两段，代价为两段木头长度的乘积。

思路：数学计算

假设长度为 n，切割的第一段为 x，则另一段长度为 n-x，代价为 x * (n-x)。
这是一个一元二次方程，开口朝下，所以中心点 n/2 的代价最大，两个解x=0 与 x=n代价最小。

根据曲线可以发现，x 小于中心时，x 越小代价越小，或者 x 大于中心时，x 越大代价越小。
当然，两个是基于中心对称的，所以是等价的。

所以，假设只分割两段，这里直接取 x=k 就是最优值。

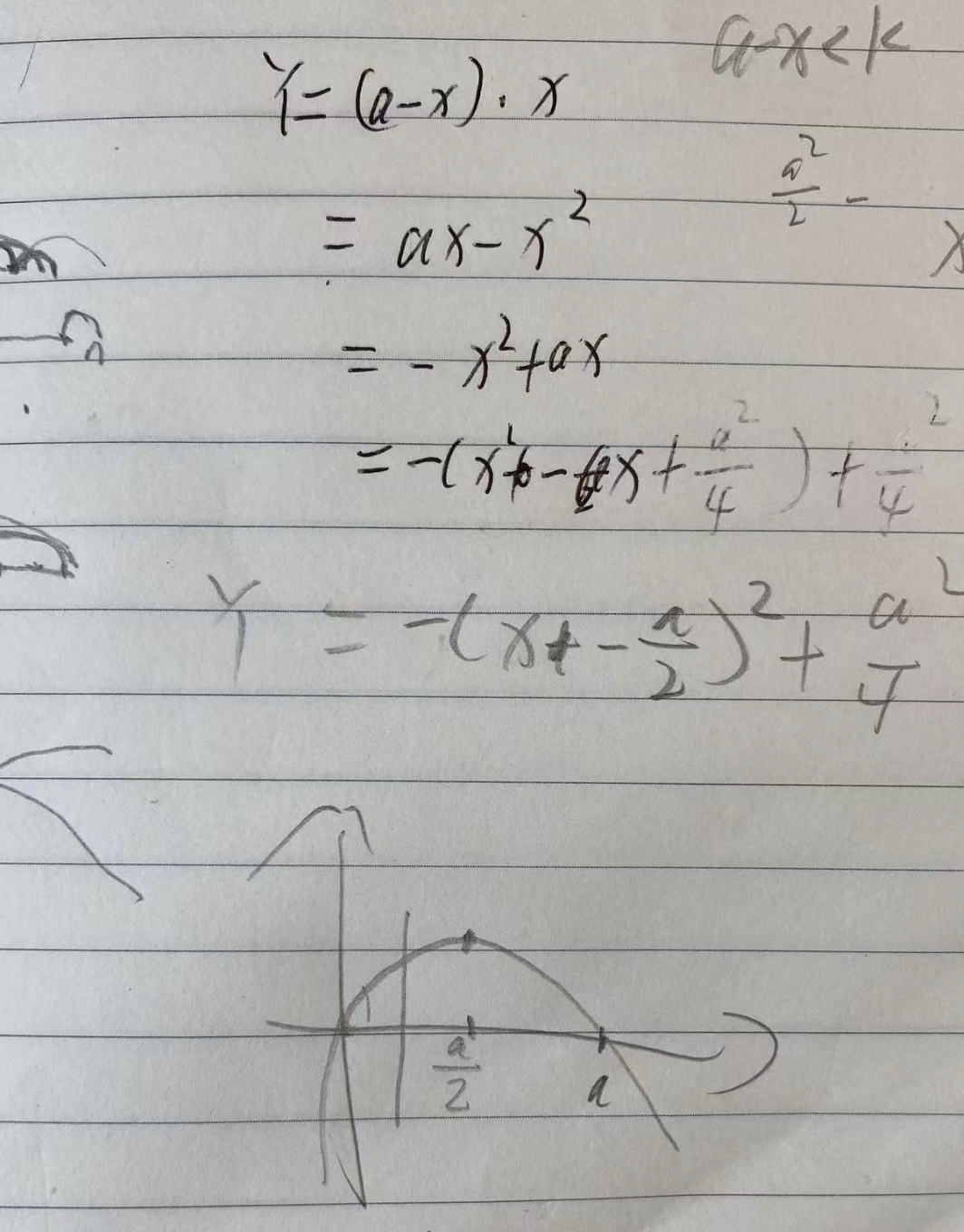
怎么证明最分割两段是最优的呢？
比赛的时候我是直接找一个例子看的。

假设分割两段，最优代价是 k * (n-k)。
假设分割多段，例如三段，第一次分割显然大于 k，不妨设长度为 k+x，第二次按最优分割，即为 k。
则分割三段的最优代价是 (k+x) * (n - (k+x)) + k*x。

相关相减，可以证明，两段是更优的。

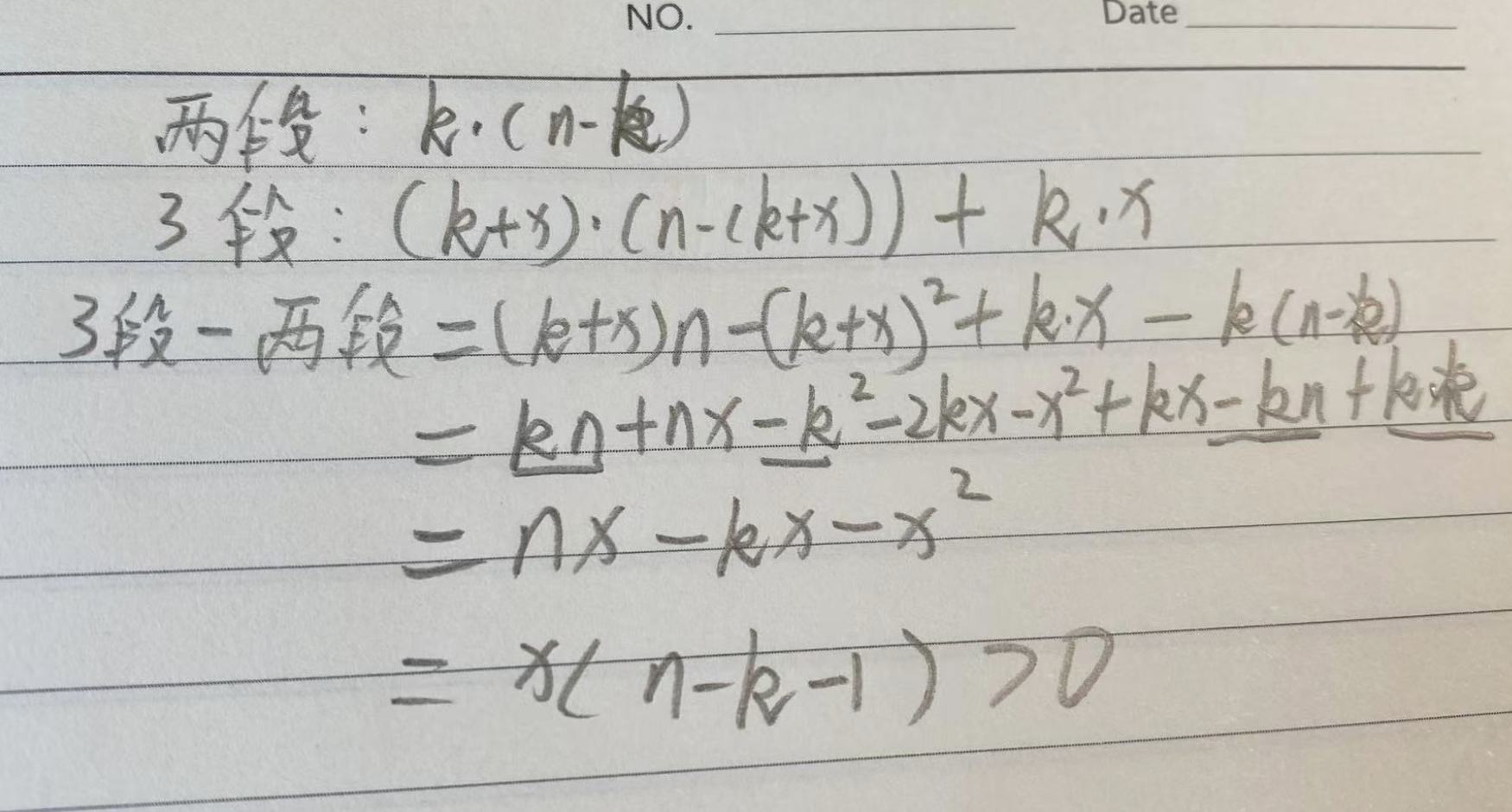
故可以大胆猜测，分割两段是最优的。
故可以下面的贪心公式。

ll C(ll n, ll k) {  //
  if (k >= n) return 0;
  return k * (n - k);
}

二、移除相邻字符

题意：给一个字符串，要求不断地删除最左边的两个连续字符，求最后得到的字符串。
连续字符定义：字母表循环相邻时称为连续。

思路：栈。

维护一个栈，判断两个是否连续即可。

for (auto c : s) {
  if (!ans.empty() && Check(c, ans.back())) {
    ans.pop_back();
  } else {
    ans.push_back(c);
  }
}

三、折扣价交易股票的最大利润

题意：给一个树形组织架构，每个员工最多可以买卖一次股票。
如果父节点有买卖操作，则子节点可以半价买入的股票。
现在告诉你每个员工的初始股票买入价格与卖出价格，以及总的资金，问员工怎么操作才能收益最大化。

思路：树形DP

状态定义：f(u,flag,B) 父节点买股票状态为flag时，子树u 投入资金 B 的最大收益。

状态转移方程： 分为子树根 u 的买入与不买入。

不买入，则枚举所有儿子分配资金 B 的最优答案。
买入时，需要能够买入，然后枚举所有儿子分配剩余资金 B-b 的最优答案。

// 不选择
ret = DfsChild(u, 0, G[u].size(), B);

// 选择
int buy = present[u];
if (preFlag) {
  buy = present[u] / 2;
}
if (buy <= B) {  // 能买才买
  int tmp = future[u] - buy;
  tmp += DfsChild(u, 1, G[u].size(), B - buy);
  ret = max(ret, tmp);
}
return ret;

儿子如何分配资金 B 呢？
使用另外一个动态规划，即枚举每个儿子分配若干资金后，整体的最优答案。

状态定义：F(u, flag, m, B) 父节点 u 买入股票状态为 flag 时，父节点u 的前 m 个儿子共投入资金 B 时的最优答案。

状态转移方程：第 m 个儿子分配资金 b，前面的儿子分配资金 B-b时的最优答案。

ret = 0;
// 最后一个儿子所在子树给多少钱
const int v = G[u][m - 1];
for (int b = 0; b <= B; b++) {
  int tmp = DfsChild(u, preFlag, m - 1, B - b) + Dfs(v, preFlag, b);
  ret = max(ret, tmp);
}
return ret;

预估最坏复杂度：n^2 * B^2
分析：树最多 n-1个边，故枚举最后一个儿子顶多 n-1次，不会是 n^2次。
实际复杂度：n*B^2

四、移除相邻字符后字典序最小的字符串

题意：给一个字符串，问移除任意次的相邻连续两个字符，求使得剩余的字符串的字典序最小。

思路：枚举动态规划。

注意，这道题是求字典序最小的串，不是求删除次数最多的串。

字典序最小，代表第一个字母最小。
故可以先看答案的第一个字母，显然越小越好。

假设第一个字母为 x，则 x 前面的字符串显然需要通过两两连续消除掉。
故问题转化为了判断一个子串是否可以两两消除，这个可以动态规划来做。

假设已经有一个 Solver(l,r) 来判断这个子串是否可以消除掉。
则需要枚举所有字符，，判断前缀字符串是否可以两两消除，可以了，这个字符就是消除前缀后剩余的第一个字符。
显然，需要保留字符最小的那个。
同时，最小的字符可能出现多次，故还需要记录出现的位置。

第一个字符可能出现多个位置，故对于第二个字符，需要在所有这些位置去进行重复的操作，找到第二个位置最小的的字符。

set<int> pre; // 上个字符所有出现的位置列表
pre.insert(0);  
while (!pre.empty()) {
  set<int> now;  // 下一轮位置列表
  char minChar = 'z' + 1;
  for (auto firstPos : pre) {
    if (Solver(firstPos, n - 1)) {
      return ans; // 后缀都可以消除，消除最优
    }
    for (int i = firstPos; i < n; i++) {
      if (!Solver(firstPos, i - 1)) {
        continue;
      }
      char c = s[i];
      if (c < minChar) {  // 更新最小的字符
        minChar = c;
        now.clear();
      }
      if (c == minChar) {  // 记录相同的字符的位置
        now.insert(i + 1);
      }
    }
  }
  ans.push_back(minChar);
  pre.swap(now);  // 下一轮状态
  if (!now.empty() && *pre.rbegin() == n) {
    break; // 选择 minChar 后，剩余的后缀可以消除
  }
}

那怎么快速判断一个子字符串是否可以全部消除呢？

如果一个字符串可以完全消除，只能分为两种情况。

情况1：中间的先消除，最后收尾消除。
情况2：分成两段，分别独立的全部消除，这里需要枚举分割线。

int Solver(int i, int j) {
  if (j < i) return 1;   // 空串
  if (dp[i][j] != -1) {  // 记忆化
    return dp[i][j];
  }
  int len = j - i + 1;
  if (len % 2 == 1) {
    return dp[i][j] = 0;  // 奇数不可能被消除
  }
  if (len == 2) {
    return dp[i][j] = Check(s[i], s[j]);
  }
  // 情况1：首位匹配 + 中间匹配
  if (Check(s[i], s[j]) && Solver(i + 1, j - 1)) {
    return dp[i][j] = 1;
  }
  // 情况2：分割线，左右匹配
  for (int k = i + 1; k < j; k++) {
    if (Solver(i, k) && Solver(k + 1, j)) {
      return dp[i][j] = 1;
    }
  }
  return dp[i][j] = 0;
}

子串判断复杂度：O(n^3)
构造答案复杂度：O(n^3)
综合复杂度：O(n^3)

五、最后

这次比赛后两题算是有难度，不过涉及的算法还是可以想到的。
我比赛期间读完题，都很快想到了解法，但是敲代码速度有点慢，最终比赛期间没有通过，比较可惜。

《完》

-EOF-

本文公众号：天空的代码世界
个人微信号： tiankonguse
公众号 ID： tiankonguse-code