CCF CSP-J 2024 第二轮入门级认证
作者: | 更新日期:
第四题难度飙升
本文首发于公众号:天空的代码世界,微信号:tiankonguse
零、背景
最近打算做一下 CSP-J 与 CSP-S 的比赛题,第一场就做 2024 年的入门级比赛吧。
A: 统计
B: 模拟
C: 找规律贪心
D: 线性DP
代码地址: https://github.com/tiankonguse/leetcode-solutions/tree/master/other/CSP-J/
一、扑克牌
题意:给你一些扑克牌,问至少需要再给你几张牌,才能凑够一副完整的扑克牌。
思路:统计
集合去重,看自己有多少张,与完整扑克牌总数求差即可。
unordered_set<string> H;
char str[4];
void Solver() { //
ll n;
scanf("%lld", &n);
while (n--) {
scanf("%s", str);
H.insert(str);
}
ll ans = 52 - H.size();
printf("%lld\n", ans);
}
二、地图探险
题意:给你一个地图,某些位置有障碍物。现在你在一个起始位置和一个方向,问进行 k 次操作可以到达哪些不同位置。
规则:默认按当前方向向前走一步,如果下一步无法走,则右转。右转算一次操作。
思路:模拟
按题意模拟,记录下经过的坐标,求和。
小技巧:地图可以新增一个特殊字符,来标记是否到达过。
第一次到达后,标记一下,只有第一次到达时答案才加一。
char str[1010][1010];
int dir[4][2] = { {0, 1}, {1, 0}, {0, -1}, {-1, 0}};
ll ans = 0;
void Add(int x, int y) {
if (str[x][y] == '.') {
str[x][y] = 'y';
ans++;
}
}
Add(x, y);
while (k--) {
int X = x + dir[d][0];
int Y = y + dir[d][1];
if (X < 1 || X > n || Y < 1 || Y > m || str[X][Y] == 'x') {
d = (d + 1) % 4;
} else {
x = X;
y = Y;
}
Add(x, y);
}
printf("%lld\n", ans);
三、小木棍
题意:如下图,需要使用 n 个火柴摆出一个正整数,求可以摆出的最小正整数。
如果火柴无法摆出数字,则返回 -1。
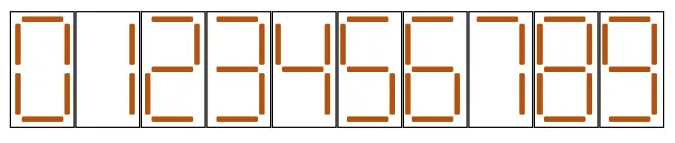
思路:找规律。
分析所有数字需要的火柴数量,然后按数量分类,如下,至少需要 2 根,最多需要 7 根。
2: 1
3: 7
4: 4
5: 2, 3, 5
6: 0, 6, 9
7: 8
第一步是分析什么场景会没有答案。
分析发现,除了 1 根火柴无法摆出数字,其他的都可以摆出来。
例如 2个火柴一组,如果还剩余一根,则最后一个数字使用三根来摆。
第二步是分析怎么摆出最小的数字。
想要正整数最小,位数就需要尽量的小,所以每个位置需要消耗的火柴数量需要尽量的多。
所以答案的位数肯定是 (n+6)/7 位,且低位都是 8。
针对不同的余数,我们做不同的特殊处理。
余数为0:完美,数字全是 8。
余数为1:1无法摆出数字,下一位需要借位,这样就有 8 根火柴来组成最小的两位数字,可以发现是 10。
余数为2:可以摆出 1, 1 是最小数字,后面跟若干个 8。
余数为3:可以摆出 7。
如果下一位借位,是可以摆出 2 为前缀的数字的。
前两位有 10 个火柴,最高位是 2 时占用 5 根,剩余5跟可以摆出 2,即前缀是 22。
此时如果存在下下位,则也借位,则第二位可以摆成 0,得到更小的前缀 200。
故余数为 3 分三种情况:3根火柴摆出 7,10根火柴摆出 22,更多火柴摆出 200 前缀。
余数为4,可以摆出 4。
同样,下一位借位,共 11 根火柴,可以摆出 20。
余数为5,可以摆出 2,已经最小了。
余数为6, 最小的正整数是 6,已经最小了。
总结:10 根火柴以内,需要特殊处理,10 根以后,答案只剩余一种情况,直接拼出答案。
void Dump(ll val, ll b) {
if (val) {
printf("%lld", val);
}
for (ll i = 0; i < b; i++) {
printf("8");
}
printf("\n");
}
ll one[] = {-1, -1, 1, 7, 4, 2, 6, 8, 10, 18, 22, 20};
ll a = n % 7;
ll b = n / 7;
if (n < 11) {
printf("%lld\n", one[n]);
continue;
}
if (a == 0) { // 整除,此时 b 肯定大于0
Dump(0, b);
} else if (a == 1) {
Dump(10, b - 1);
} else if (a == 2) {
Dump(1, b);
} else if (a == 3) {
Dump(200, b - 2);
} else if (a == 4) {
Dump(20, b - 1);
} else if (a == 5) {
Dump(2, b);
} else if (a == 6) {
Dump(6, b);
}
四、接龙
题意:n 个人,每个人有一个长度为 L 的数字序列,大家开始进行接龙。
规则1:连续两个接龙的人不能相同。
规则2:下个人接龙的数字系列的第一个数字,需要与上个人接龙的最后一个数字相同。
规则3:接龙的数字序列为一个连续子串,且长度至少为 2,至多为 K。
规则4:第一轮使用数字1开始接龙。
规则5:Q个询问,每个询问问第 R 轮接龙后的最后一个数字是否是 C。
数据范围:如下图。

思路:线性DP
最笨的方法: 模拟
1)储存上一轮结尾的数字集合,以及这些数字是哪些人接龙的。
2)枚举每个人的每个数字序列的位置,判断是否可以接龙,复杂度O(N*L*N)。
3)可以拉,接下里 K 个数字都是可以到达的位置,进行标记,复杂度 O(K)。
4)聚合标记的位置,得到这一轮结尾的数字集合,以及对应的人。
综合复杂度:O(R*N^2*L*K)
优化0:常数优化。
如果使用二维 vector 或者邻接表储存二维数组,发现及时做了后续的所有优化,还是会超时。
需要使用一位数组表示二维数组,就不会超时了。
复杂度:不变。
int n, k, q;
vector<pair<int, int>> nums(2 * N);
vector<pair<int, int>> ranges(N); // 计算每个人的数字在所有数字里面的范围,[piLeft, piRight)
int maxR;
int maxOffset = 0;
scanf("%d%d%d", &n, &k, &q);
for (int i = 0, offset = 0; i < n; i++) {
int l;
scanf("%d", &l);
for (int j = 0; j < l; j++, offset++) {
int S;
scanf("%d", &S);
maxS = max(maxS, S); // 记录最大的值
nums[offset] = {i, S};
}
ranges[i] = {maxOffset, maxOffset + l};
maxOffset += l;
}
优化1:每个结尾的数字不需要储存所有的接龙人。
规则只是要求接龙的人不同,如果接龙的人大于等于2人,那这个数字肯定所有人都是可以接龙的。
优化后复杂度:O(R*N*L*K)
小技巧:可以使用一维数组,使用一个负数来标记是否是多个人。
vector<int> preFlag(2 * N, -1); // 上一轮接龙时,记录每个值结尾的有哪些人,-1 代表有多个人,否则是人的编号
if (preFlag[S] == -1) {
preFlag[S] = i; // 记录这个值可以结尾
} else {
if (preFlag[S] != i) { // 如果已经有了,说明有多个人接龙到这个值
preFlag[S] = -2; // 标记为多个人
}
}
优化2:接龙后,标记 K 个数字可以优化。
最容易想到的是线段树,区间标记。
为了方便下标选择,也可以使用权值线段树。
当然,这个操作复杂度有一个 log,实际会超时的。
vector<int> preFlag(2 * N, -1); // 上一轮接龙时,记录每个值结尾的有哪些人,-1 代表有多个人,否则是人的编号
fill(preFlag.begin(), preFlag.end(), -1); // 初始化 preFlag
preFlag[1] = -2; // 初始状态,1 号值可以开始接龙
for (int r = 1; r <= maxR; r++) { // 进行 R 轮游戏
for (int offset = 0; offset < maxOffset; offset++) {
auto [pi, S] = nums[offset];
const auto [piLeft, piRight] = ranges[pi]; // [piLeft, piRight)
if (pi == preFlag[S] || preFlag[S] == -1) continue; // 不能接自己的
if (offset + 1 == piRight) continue; // 不能接到最后一个
int left = offset + 1;
int right = min(offset + k - 1, piRight - 1); // 下一个值
Update(r, pi, left, right); // 第 r 轮,第 pi 个人,从 left 到 right 接龙的结束位置
}
Merge(r); // 第 r 轮结束后,合并所有人的接龙结果
}
实际上,区间标记,最经典的方法是标记法,即左加右减法。
这样全部标记后,最后扫描一遍,即可知道哪些标记了。
优化后复杂度:O(R*N*L)
vector<int> preFlag(2 * N, -1); // 上一轮接龙时,记录每个值结尾的有哪些人,-1 代表有多个人,否则是人的编号
// 这里方法很多,例如线段树、权值线段树、树状数组、递减标记法、左加右减标记法
// 这里采用左加右减标记法
vector<int> flags(2 * N, 0);
inline void Update(int r, int pi, int left, int right) { // [left, right]
flags[left]++;
flags[right + 1]--;
}
void Merge(int R) {
int nowVal = 0;
fill(preFlag.begin(), preFlag.end(), -1);
for (int offset = 0; offset < maxOffset; offset++) {
auto [i, S] = nums[offset];
nowVal += flags[offset]; // 累计计算,判断当前位置是否标记
flags[offset] = 0; // 清空标记数组,避免额外 O(N)的时间初始化
if (nowVal > 0) {
if (preFlag[S] == -1) {
preFlag[S] = i; // 记录这个值可以结尾
} else {
if (preFlag[S] != i) { // 如果已经有了,说明有多个人接龙到这个值
preFlag[S] = -2; // 标记为多个人
}
}
}
}
flags[maxOffset] = 0; // 最后一个置空,这个BUG调试了1个小时
}
当然,除了左加右减的标记法,还有递减标记法。
int valFlag[2 * N]; // 上一轮接龙时,记录每个值结尾的有哪些人,-1 代表有多个人,否则是人的编号
// 这里方法很多,例如线段树、权值线段树、树状数组、递减标记法、左加右减标记法
// 这里采用递减标记法
int posflag[2 * N];
inline void Update(int R, int pi, int left, int right) { // [left, right]
int K = right - left + 1;
posflag[left] = max(posflag[left], K); // 代表接下来 posflag[left] 个人都会标记
}
void Merge(int R) {
int nowVal = 0;
memset(valFlag, -1, sizeof(valFlag));
for (int offset = 0; offset < maxOffset; offset++) {
auto [i, S] = nums[offset];
nowVal = max(nowVal - 1, posflag[offset]); // 由于是递减标记,上个递减与这个取最大值
posflag[offset] = 0; // 清空标记数组
if (nowVal > 0) {
if (valFlag[S] == -1) {
valFlag[S] = i; // 记录这个值可以结尾
} else {
if (valFlag[S] != i) { // 如果已经有了,说明有多个人接龙到这个值
valFlag[S] = -2; // 标记为多个人
}
}
}
}
}
五、最后
CSP-J 2024 的入门级比赛,前三题确实挺简单的,最后一题就比较难了。
我一开始想的线段树,后来想的是左加右减标记法,不过总是超时。
最后把二维数组修改为一维数组后,最终才通过这道题。
这里卡常数就没意思了。
不过看其他题解时,学到了递减标记法,还是有收获的。
《完》
-EOF-
本文公众号:天空的代码世界
个人微信号: tiankonguse
公众号 ID: tiankonguse-code
本文首发于公众号:天空的代码世界,微信号:tiankonguse
如果你想留言,可以在微信里面关注公众号进行留言。
