CCF CSP-S 2024 第二轮比赛
作者: | 更新日期:
第四题好难
本文首发于公众号:天空的代码世界,微信号:tiankonguse
零、背景
最近打算做一下 CSP-J 与 CSP-S 的比赛题。
之前已经写了《CSP-J 2024》的四道题的题解,今天来看看 2024 CSP-S 的四道题的题解吧。
A: 快慢指针
B: 区间问题
C: 贪心+动态规划+前缀和
D: 树形DP
代码地址: https://github.com/tiankonguse/leetcode-solutions/tree/master/other/CSP-S/
一、决斗

题意:各一个数组,对于每个位置,可以随意选择另外一个位置,如果对方的值小于当前的值,则对方可以被杀死。
问如何选择,才能使得剩余未被杀死的位置最少。
思路:二分查找 或快慢指针
显然,需要排序,然后需要从最小或者最大的开始处理。
一开始有一个集合,代表所有数字都未被杀死。
假设从最小的开始枚举,则每次只需要判断集合里最小的元素是否可以被杀死即可。
这时候,集合是顺序访问的,所以可以使用数组来储存,枚举的是快指针,尚未杀死的最小值就是慢指针。
int l = 0, r = 1;
while (r < n) {
if (nums[r] > nums[l]) {
l++;
}
r++;
}
printf("%lld\n", r - l);
假设从最大值开始枚举,则每次需要找到小于最大值的最大元素。
这个需要使用二分查找。
multiset<ll> H;
ll ans = n;
for (int i = n - 1; i >= 0; i--) {
ll v = nums[i];
auto it = H.lower_bound(v);
if (it == H.begin()) {
continue; // 没有更小值,无法删除
}
it--;
H.erase(it);
ans--;
}
printf("%lld\n", ans);
二、超速检测

题意:给一段长度为 L 的路,一开始有 n 个车以指定起点以及指定起始速度在从南往北行驶。
另外这些车还有自己的加速度,负数代表减速。
车的速度为0时停止,否则直到开出这段路。
现在路上有 m 个监控,车以超过 V 的速度超过某个监控,则算拍到超速,问哪些车会被抓拍到超速。
另外,最多关闭多少个监控,抓拍到的超速的车辆不会漏。
思路:区间问题。
第一步是计算出每个车的超速路段。
超速路段计算需要解方程。
起始速度 v, 加速度 a,目标速度 V,则需要时间 t=(V-v)/a。
行驶距离是:(v+V)*t/2。
假设计算出来的是浮点数,例如 7.4,再位置 7 不会超速,位置 8才超速。
假设计算出来的的是整数,例如7,则同上,位置 7 不会超速,位置 8才超速。
所以上面的公式直接按整数向下取整加一即可。
for (ll i = 0; i < n; i++) {
ll d, v, a;
scanf("%lld%lld%lld", &d, &v, &a);
if (a > 0) {
if (v > V) { // 起始超速,结束超速
nums0.push_back({d, L});
} else {
ll S = (V + v) * (V - v) / (2 * a) + 1;
if (d + S > L) { //行驶 S 距离超过 V
continue;
}
nums0.push_back({d + S, L});
}
} else if (a < 0) { // 减速
if (v <= V) {
continue; // 起始未超速
}
a = -a;
ll S = (V + v) * (v - V) / (2 * a);
if (S * 2 * a == (V + v) * (v - V)) {
S--;
}
nums0.push_back({d, min(L, d + S)});
} else { // 匀速
if (v <= V) {
continue;
}
nums0.push_back({d, L});
}
}
之后二分查找来判断这个路段是否有摄像头即可判断这个车是否可以被抓拍到。
nums1.reserve(n); // 被拍到的车辆
for (auto [l, r] : nums0) {
auto it = lower_bound(caremas.begin(), caremas.end(), l);
if (it == caremas.end()) {
continue;
}
if (*it > r) {
continue;
}
nums1.push_back({l, r});
}
计算出了每个车超速的路段区间后,问题转化为了选最少得点,覆盖所有区间。
区间覆盖,典型的排序扫描法。
先以右区间排序,相等时左区间排序。
sort(nums1.begin(), nums1.end(), [](auto& a, auto& b) {
if (a.second == b.second) {
return a.first > b.first;
} else {
return a.second < b.second;
}
});
第一个区间的右端点之前,必然有摄像头。
选择右端点之前的最后一个摄像头,其他摄像头都可以关闭。
摄像头选择之后,把连续覆盖的所有区间都删除。
之后重复上面的操作即可。
ll ans = caremas.size();
ll ni = 0;
ll ci = 0;
while (ci < caremas.size() && ni < nums1.size()) {
while (ci + 1 < caremas.size() && caremas[ci + 1] <= nums1[ni].second) {
ci++; // 选择区间内的最后一个摄像头
}
ans--;
while (ni < nums1.size() && caremas[ci] >= nums1[ni].first) {
ni++; // ci 摄像头可以拍到的所有车辆
}
ci++; // 跳过被选择的摄像头
}
三、染色

题意:给一个数组,要求分成两个子序列,得分规则如下:
如果同一个子序列中 S[i] 与前一个元素 S[i-1] 相等,则位置 i 的 S[i] 分,否则不得分。
问如何拆分子序列,才能得分最大。
思路:贪心+动态规划+前缀和
贪心分析:假设 S[i]在第一个子序列中。
如果 S[i]要得分,则前一个元素必须相等,可能是前面所有值相等的元素。
假设选择的不是上一个最近的元素,不妨假设选择的是上上个元素。
令上个相同元素为 S[i-1],上上个元素为 S[i-2]。
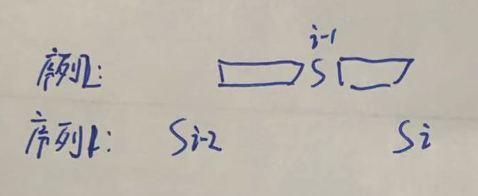
此时,S[i-2]与 S[i]之间的元素都在第二个序列中。
则 S[i-1] 肯定无法得分,因为前后相同元素都在第一个序列中,而且S[i-1]在第二个序列中没有任何价值。
如果把 S[i-1] 从第二个序列中删除,则第二个序列可能得更高分,第一个序列也会的更高分,从而总得分会更高。
由此可以证明,如果 S[i]要得分,必然是相邻的前一个相同元素贡献分时才会最优。
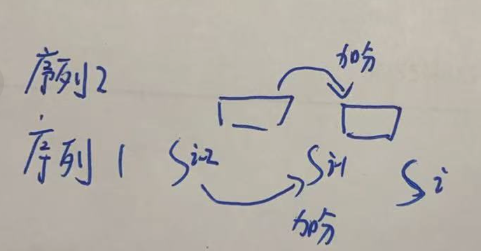
有了上面的贪心结论,就可以动态规划来做这道题了。
状态定义:dp(n,c) 第 n 个元素在第 c 个子序列时,前 n 个元素的最优拆分。
对于第 n 个元素,可以选择得分与不得分。
如果不得分,则与前面的元素没关系,前一个元素可能属于任何一个子序列。
dp(n,c) = max(dp(n-1, 0), dp(n-1, 1));
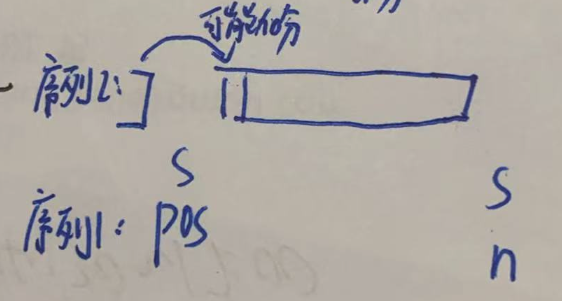
如果得分,假设最近的值相等的位置为 pos,则两个位置之间的其他元素都在另外一个序列,得分是确定下的,可以预处理单独计算。
唯一的不确定是 pos 前一个元素,也可能在自己的子序列里与前面的值一样,从而得分。
故如果存在这样的位置,需要从 pos 前一个位置开始递归。
dp(n,c) = S[n] + Range(pos+1, n-1) + Dfs(1^c, pos+1);
具体代码如下
if (P[pos] != 0) {
int lastPos = P[pos];
ll tmp = A[pos] + Range(lastPos + 1, pos - 1);
if (lastPos + 1 != pos) {
tmp += Dfs(color ^ 1, lastPos + 1);
} else {
tmp += Dfs(color, lastPos);
}
ans = max(ans, tmp);
}
对于连续序列的得分,可以通过预处理前缀和快速计算。
ll Range(int l, int r) {
if (l >= r) return 0;
return B[r] - B[l];
}
四、擂台游戏

题意:2^k个人比赛,每轮淘汰一半人,最后剩余一个人,典型的一个完全二叉树。
胜出的规则抽签决定,抽到谁后,如果这个人的能力值大于比赛轮数,则这个人获胜,否则对手获胜。
现在人数不足 2^k个,只有 n 个人,我们需要补充几个选手,能力值任意,使得选手人数满足2^k。
现在问是否可以通过调整补充选手的能力值,使得指定编号选手获胜。
求所有可能获胜选手的编号之和。
另外,题目有多个提问,即每次假设只有前 x 个选手到达,其他选手需要补充,分别求上面的编号之和。
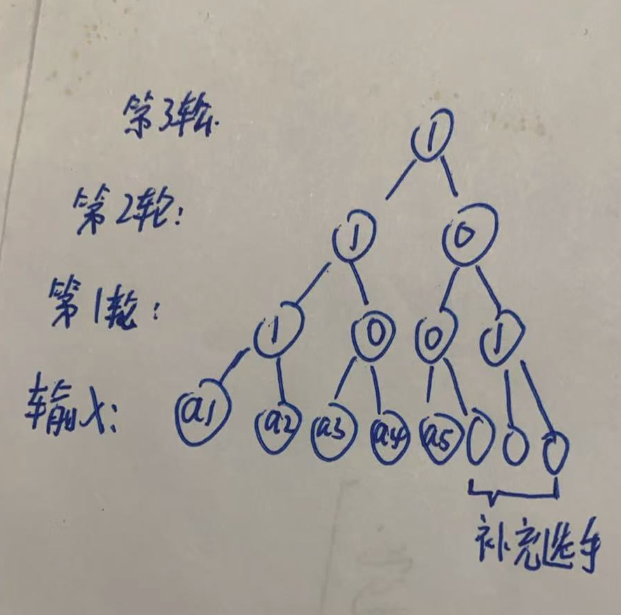
思路:题目很复杂,理解题目就需要消耗不少时间。
理解题目之后,发现这道题并不难。
按题意输出输入 n 个选手的能力值、m 个询问,以及完全二叉树的抽闲结果。
void Input() {
scanf("%d%d", &n, &m);
K = UpPow(n);
dataOffset = 1 << K;
for (int j = dataOffset, i = 1; j < 2 * dataOffset; j++, i++) {
A[j] = {0, i}; // 最底层默认全部设置为0
}
for (int i = 1, j = dataOffset; i <= n; i++, j++) {
scanf("%lld", &AA[i]);
A[j] = {AA[i], i};
}
for (int i = 1; i <= m; i++) {
scanf("%lld", &C[i]);
}
for (int k = K - 1, offset = dataOffset; k >= 0; k--) {
scanf("%s", str);
const int step = 1 << k;
offset -= step;
for (int j = 0; j < step; j++) {
flag[offset + j] = str[j] - '0'; // 将字符转换为数字
}
}
}
然后每组数据,重新初始化计算各个选手的初始能量值。
void Reinit() {
// O(n) 计算输入数据
for (int i = 1, j = dataOffset; i <= n; i++, j++) {
A[j] = {AA[i] ^ X[i % 4], i};
}
// O(n) 计算已确定答案的数据
for (int k = K - 1, offset = dataOffset; k >= 0; k--) {
const int step = 1 << k;
const int R = K - k; // 比赛轮数,是逆序的,从编号 1 开始
offset -= step;
for (int j = 0; j < step; j++) {
const int no = offset + j;
const int v = flag[no];
if (A[no * 2 + v].first >= R) {
A[no] = A[no * 2 + v];
} else {
A[no] = A[no * 2 + (v ^ 1)];
}
}
}
}
主函数大概如下,逐个进行询问,计算答案。
int t;
void Solver() { //
Input();
scanf("%d", &t);
while (t--) {
for (int i = 0; i < 4; i++) {
scanf("%lld", &X[i]);
}
Reinit();
ll ans = 0;
for (int i = 1; i <= m; i++) {
ans ^= Query(C[i]) * i;
}
printf("%lld\n", ans);
}
}
查询的时候,根据查询的队员个数,可以确定一条不确定路径,路径的高度是树高,故每次查询的复杂度是 log(n)。
树父节点与子节点的关系分为八种情况来讨论是否可以获胜。
简单情况1:叶子节点,确定的能力值。
如果父路径中某一轮需要进行抽签判断,则需要大于对应的轮数,这个节点才能获胜。
if (p >= dataOffset && p <= queryOffset) {
if (A[p].first >= minVal) { // 可以获胜整个比赛
sum += A[p].second;
}
return {A[p].first, -1}; // 最小获胜值是 A[p].first,-1 代表没有右区间,只有一个答案
}
简单情况2:叶子节点,补充的能力值。
此时把能力值设置为无穷大,必然获胜,
if (p >= dataOffset && p > queryOffset) {
sum += leftNo; // 空闲节点,可以选择无限大从而获胜
return {0, 0}; // [0,inf] 都是答案,最小值是 0
}
简单情况3:子树全部是确定的能力值。
子树的能力值是固定的,所以子树中哪个能力值胜出也是确定的。
如果父路径中某一轮需要进行抽签判断,则需要大于对应的轮数,这个子树才能获胜。
if (queryOffset >= rightOffset) { // 所有队员都是确定的,答案是确定的
if (A[p].first >= minVal) { // 可以获胜整个比赛
sum += A[p].second;
}
// 最小获胜值是 A[p].first,-1 代表没有右区间,只有一个答案
return {A[p].first, -1};
}
简单情况4:子树全部是补充的能力值。
所有位置都可能获胜,想要谁获胜,对应节点的能力值就设置为无穷大,其他节点设置为无穷小即可。
// 所有队员都是空的,任意位置都可以胜出, 且胜出的能量值可以是所有大于等于0的值
if (queryOffset < leftOffset) {
sum += RangeSum(leftNo, rightNo);
return {0, 0};
}
复杂情况5:左子树都是确定能力值,左子树抽签。
由于左子树的能力值是确定的,所以左子树胜出的能力值也是确定的,所以左子树的抽签结果也是确定的。
抽签赢了,就返回左子树,否则就是输了,返回右子树。
auto [leftMinWinVal, leftRangeWinVal] = Dfs(p * 2, R - 1, max(minVal, R));
if (leftMinWinVal < R) { // 左子树必输
return Dfs(p * 2 + 1, R - 1, minVal);
} else { // 左子树必赢,不需要看右子树了
return {leftMinWinVal, leftRangeWinVal};
}
父路径需要是否需要抽签
在简单情况中,多次提到【如果父路径中某一轮需要进行抽签判断,则需要大于对应的轮数,这个子树才能获胜】。
那怎么知道父路径是否需要抽签判断了?
递归的时候,父节点是知道这个信息的,当一个子树需要抽签判断时,就把对应的轮数带下来。
由于可能父路径有多轮都需要抽签判断,所以需要对轮数取最大值max(minVal, R)。
复杂情况6:左子树都是确定能力值,右子树抽签。
右子树抽签后,怎么才能让左子树是否能够获胜呢?
显然,如果右子树最后胜出的能力值小于当前轮数,则右子树抽签输掉,从而能把主动权交给左子树。
所以,递归的时候,需要返回当前子树能够胜出的最小能力值。
auto [rightMinWinVal, rightRangeWinVal] = Dfs(p * 2 + 1, R - 1, max(minVal, R));
if (rightMinWinVal < R) { // 右子树可以输比赛
auto [leftMinWinVal, leftRangeWinVal] = Dfs(p * 2, R - 1, minVal);
}
返回值的讨论
假设左右子树胜出的最小能力值是R-1,当前轮数是 R,则当前子树胜出的最小能力值就变成 R了。
假设左右子树胜出的最小能力值是 R+a,当前轮数依旧是 R,则当前子树胜出的最小能力值就是 R+a了。
由此,可以发现不仅要保留胜出的最小能力值,还需要保留所有能力值集合,从而能与当前轮数比较后,得到最新的最小能力值。
分析抽签数,可以发现,
子树都是确定能力值时,能力值集合大小为1,就是最终胜出的那个能力值。
如果需要抽签判断,胜出集合不变,输了集合变空。
子树全部是补充能力值时,能力值集合是 [0,inf]。
如果需要抽签判断,肯定可以胜出,能力值集合转化为 [R, inf],随后父路径的不断抽签判断,区间的边界会越开越大。
但是对于当前的复杂情况6:左子树都是确定能力值,右子树抽签
如果右子树都是补充的,最小能力值是 0,故可以把选择权交给左子树。
如下图,如果左子树胜出的能力值小于当前轮数,则当前子树最终胜出的能力值就分两段,一个是单点,一个是区间。
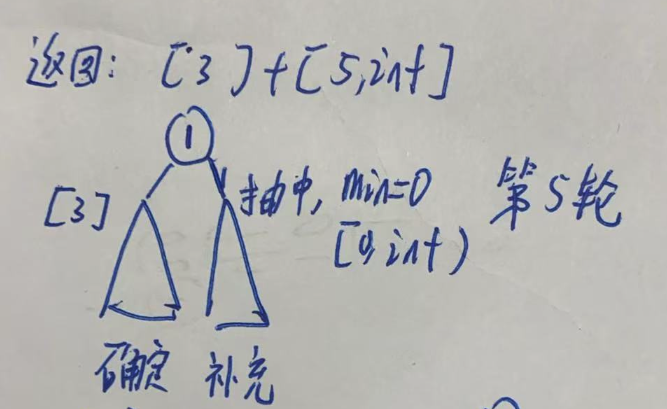
那会不会后面变成多个单点加一个区间呢。
枚举一下,发现不存在这样的情况。
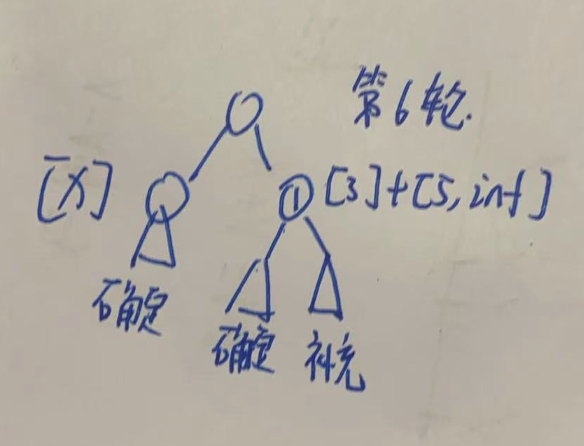
由于当前的左子树已经是全部确定的,所以如果当前子树是父节点的右子树,则父节点的左子树肯定也都是确定的,不妨设胜出的能力值为 x。
如果抽签抽到右子树,则右子树胜出后的能量值是 [6,inf]。
如果主动失败把选择权给左子树,则最终还是一个单点[x]与一个区间 [6,inf],另外如果 x大于6,则还需要更新最小值为 6。
如果抽签抽到左子树,想要胜出,必须大于 6,此时右子树必败,父节点的能力值就是 x。
不是胜出就是失败,此时右子树的能量值保持不变,为一个单点3与一个区间[5,inf]。
当前子树作为父节点的左子树也是一个逻辑,不过涉及到两个区间的并集操作。
因此,每个树需要返回两个值,一个是最小能力值,一个值连续区间。
如果区间不存在,则可以使用特殊标记。
复杂情况6的完整代码如下
auto [rightMinWinVal, rightRangeWinVal] = Dfs(p * 2 + 1, R - 1, max(minVal, R));
if (rightMinWinVal < R) { // 右子树可以输比赛
auto [leftMinWinVal, leftRangeWinVal] = Dfs(p * 2, R - 1, minVal);
MyAssert(leftRangeWinVal == -1);
if (rightRangeWinVal == -1) { // 右子树只有一个能力值,还输掉比赛,答案是左子树
return {leftMinWinVal, leftRangeWinVal};
}
// 右子树可能是 <R-a, R+b> , 此时右子树胜出时的最小值是 R+b
return {min(leftMinWinVal, max(R, rightRangeWinVal)), rightRangeWinVal};
} else {
return {rightMinWinVal, rightRangeWinVal};
}
复杂情况7:右子树全部补充,右子树抽签
// 右子树的所有编号全部是答案,构造答案:对应的编号无限大,其他都是0,则这个编号必然获胜
auto [rightMinWinVal, rightRangeWinVal] = Dfs(p * 2 + 1, R - 1, max(minVal, R));
MyAssert(rightMinWinVal == 0);
MyAssert(rightRangeWinVal == 0);
// 右子树想要获胜,能力值必须大于当前轮数 R,故能力值范围是 [R, INF]
rightRangeWinVal = R;
// 右子树选择小于等于 R 的值,把胜利权利转让给左子树, 此时子树的能力不需要大于当前轮数
auto [leftMinWinVal, leftRangeWinVal] = Dfs(p * 2, R - 1, minVal);
if (leftRangeWinVal != -1) {
rightRangeWinVal = min(rightRangeWinVal, leftRangeWinVal);
}
return {min(leftMinWinVal, R), rightRangeWinVal};
复杂情况8:右子树全部补充,左子树抽签
// 答案由左子树确定,左子树要获胜,需要大于当前轮数,还需要大于后续的比赛轮数 minVal
auto [leftMinWinVal, leftRangeWinVal] = Dfs(p * 2, R - 1, max(minVal, R));
if (leftMinWinVal < R) { // 左子树可以输掉比赛
// 右子树全部是答案, 构造答案:对应的编号无限大,其他都是0,则这个编号必然获胜
auto [rightMinWinVal, rightRangeWinVal] = Dfs(p * 2 + 1, R - 1, max(minVal, R));
MyAssert(rightMinWinVal == 0);
MyAssert(rightRangeWinVal == 0);
return {0, 0};
} else {
return {leftMinWinVal, leftRangeWinVal};
}
通过这些复杂的分情况判断,我们就可以写出时间复杂度为 O(T n log(n)) 的代码了。
但是提交后,发现只能得 84 分。

原因是这道题 T 是 256, n 是 10^5。
没有 log(n) 是 2*10^7刚好能通过。
加一个 log 就是 10^8,必然会超时了。
继续优化的方法能大概想到,即计算出一个编号的答案,从而 O(1)推导计算出下个编号的答案。
不过这个太复杂了,上面的八种情况我周末想了整整一天,最终写了三百多行代码,代码量太大了。
这道题的难度是 NOI/NOI+/CTSC 级别的,我就先做到这里,以后有时间了,再来想怎么优化吧。

五、最后
这次比赛第一题属于签到题。
第二题代码量就变大很大,先解方程计算每辆车的超速路段,然后二分找到被抓拍的车,最后区间处理删除多余的摄像头。
第三题属于景点的动态规划,不过需要能够推导出贪心策略,从而能降低动态转移方程的复杂度。
第四题题目阅读起来就很费劲,大概方向很容易想到,但是树形DP实现起来很复杂,要处理的细节太多了,最后还会超时,只有 84 分,难受。
没想到 CSP-S 最后一题的难度就这么难了,还好处于我刚好能走的难度,但是最后一题有没有完全做出来。
不知道往年的会不会稍微简单点。
《完》
-EOF-
本文公众号:天空的代码世界
个人微信号: tiankonguse
公众号 ID: tiankonguse-code
本文首发于公众号:天空的代码世界,微信号:tiankonguse
如果你想留言,可以在微信里面关注公众号进行留言。
