CCF CSP-S 2023 第二轮比赛

零、背景

最近打算做一下 CSP-J 与 CSP-S 的比赛题。
之前已经写了《CSP-J 2024》、《CSP-S 2024》、《CSP-J 2023》的题解，今天来看看 2023 CSP-S 的题解吧。

A: 枚举
B: 动态规划、next函数、前缀hash、前缀矩阵
C: 模拟
D: 二分套二分+数学公式

代码地址： https://github.com/tiankonguse/leetcode-solutions/tree/master/other/CSP-S/

里面比赛总结如下

比赛	A	B	C	D	题解
CSP-J 2024	扑克牌入门	地图探险普及−	小木棍普及/提高−	接龙提高+/省选−	题解
CSP-S 2024	决斗普及−	超速检测普及+/提高	染色提高+/省选−	擂台游戏 NOI/NOI+/CTSC	题解
CSP-J 2023	小苹果普及−	公路普及−	一元二次方程普及/提高−	旅游巴士普及+/提高	题解
CSP-S 2023	密码锁普及−	消消乐提高+/省选−	结构体提高+/省选−	种树提高+/省选−	题解

一、密码锁（lock）

题意：密码锁有五个拨圈，每个拨圈有 10 个数字，分别是 0 到 9。
假设正确密码是 X，加锁时会使用规则1或者规则2随机转动一次密码锁，从而得到锁车后的密码。
现在告诉你 N 个锁车后的密码（都是使用正确密码按规则得到的），问可能得正确密码有多少个。

规则1：选择一个拨圈转动一个角度
规则2：选择相邻的拨圈转动相同的角度。

思路：枚举

由于锁车后密码不能是自己，所以转动的位置只能是其他 9 个位置。
规则1共有 5*9=45种转动方式。
规则2共有 4*9=36种转动方式。

unordered_map<ll, ll> h;
vector<ll> base = {1, 10, 100, 1000, 10000, 100000};
const int N = 5;
const int M = 9;
ll Flap(const ll num, int i, int j) {
  int v = (num / base[i]) % 10;
  ll V = (v + j) % 10;
  return num - v * base[i] + V * base[i];
}
void SolverOne(const ll num) {
  // 1 个
  for (int i = 0; i < N; i++) {
    for (int j = 1; j <= M; j++) {
      const ll newNum = Flap(num, i, j);
      h[newNum]++;
    }
  }

  // 转动两个
  for (int i = 1; i < N; i++) {
    for (int j = 1; j <= M; j++) {
      const ll newNum = Flap(Flap(num, i - 1, j), i, j);
      h[newNum]++;
    }
  }
}

对于每个锁车后的密码，枚举所有规则的转发，得到疑似的正确密码。
最后统计所有疑似的正确密码，如果都可以有 N 个锁车后密码得到，则就是可能的正确密码。

ll ans = 0;
for (auto [k, v] : h) {
  if (v == n) {
    ans++;
  }
}
printf("%lld\n", ans);

二、消消乐（game）

题意：给一个数组，每次可以消除相邻相同的元素，问所有非空子串中，有多少个子串是可以消除的。

思路：多种解法

一个字符串是否可消除

先看思考，对于一个字符串，什么时候是可以消除的。

显然可以贪心，使用一个栈来保存剩余的未消除的前缀或后缀的字符。
如果到最后栈为空，则可以全部消除，否则不可以全部消除。

暴力解法

枚举子串的结束位置，维护一个待消除的栈，每次栈为空时，就代表当前子串是可消除的。
复杂度：O(n^2)
得分：50分

string sta;
for (int i = 0; i < n; i++) {
  sta.clear();
  for (int j = i; j >= 0; j--) {
    char c = str[j];
    if (!sta.empty() && sta.back() == c) {
      sta.pop_back();
    } else {
      sta.push_back(c);
    }
    if (sta.empty()) {
      ans++;
    }
  }
}

动态规划

状态定义：dp[i] 以位置 i 为结束位置的可消除的子串数量。

枚举每个结束位置的时候，可以发现一个规律：答案的个数其实就是最小可消除子串的个数。

假设枚举的结束位置为 i，枚举到 j 时，栈为空，此时说明 str[j...i] 时可以消除的。
如果前面枚举到 k 时，栈再次为空，说明 str[k...i] 也是可以消除的。
显然可以证明，str[k...j-1]也是可以消除的。

其实，从 j-1往前，有哪些位置是可以消除的，在位置 j-1已经计算过了。

由此，可以推导出状态转移方程：dp[i]=dp[j-1]+1
j-1为 i 前面第一个可消除的位置。

此时可以得 60 分。

string sta;
vector<ll> dp(n + 1, 0);
// dp[0] 也代表一个状态，下标从1开始计算
for (int i = 1; i <= n; i++) {
  sta.clear();
  for (int j = i; j > 0; j--) {
    char c = str[j - 1];
    if (!sta.empty() && sta.back() == c) {
      sta.pop_back();
    } else {
      sta.push_back(c);
    }
    if (sta.empty()) {
      dp[i] = 1 + dp[j - 1];
      ans += dp[i];
      break;
    }
  }
}

next数组思想

前面动态规划超时的原因是第一个循环节需要去枚举，最坏情况导致还是O(n^2)的复杂度。
那能不能不枚举呢？

此时需要分情况讨论。
如果 str[i-1] 与 str[i]相同，显然最小循环节为2，直接计算出答案。
如果不同，需要先找到以 i-1为结尾的最小循环节，这个之前也是计算过的，可以直接到最小循环节的上个位置进行匹配。

这个思想类似于 KMP 的 next 数组，比较过的，就不要比较了，快速跳过。

复杂度分析：表面上看，最坏情况还是O(n^2)。
分析每个位置 next[p]的次数，可以发现最多一次。
因为不匹配时，代表当前位置 i 可消除的范围会覆盖 p, 以后从 i 会直接跳到 p 前面。
最终复杂度：O(n)

vector<ll> dp(n + 1, 0);    //
vector<ll> next(n + 1, 0);  // [next[i], i] 可消除
for (int i = 1; i <= n; i++) {
  int p = i - 1;
  while (p > 0 && str[i - 1] != str[p - 1]) {
    p = next[p] - 1;
  }
  if (p > 0) {
    dp[i] = 1 + dp[p - 1];
    next[i] = p;
    ans += dp[i];
  }
}

前缀HASH

假设位置 i 的前缀子串尽可能的消除后，得到的字符串是 aba。
如果另外一个位置 j 的前缀子串消除后子串也是 aba。
则显然，子串 str[j+1,i] 是可以消除的。

故可以记录消除后的前缀个数，从快速计算出位置 i 为结束位置的可消除的子串数量。

很不幸，由于 hash 冲突，mod1e7 只能得 75 分， mod1e9 只能得 70 分。
两个结合起来才能通过。

unordered_map<ll, ll> h;
stack<char> sta;
ll pre7 = 0;
ll pre9 = 0;
ll ans = 0;
h[0] = 1;
for (int i = 0; i < n; i++) {
  const char c = str[i];
  const ll v = c - 'a' + 1;
  if (!sta.empty() && sta.top() == c) {
    int k = sta.size();
    sta.pop();
    pre7 = ((pre7 - v * qpow(BASE, k, mod1e7)) % mod1e7 + mod1e7) % mod1e7;
    pre9 = ((pre9 - v * qpow(BASE, k, mod1e9)) % mod1e9 + mod1e9) % mod1e9;
  } else {
    sta.push(c);
    int k = sta.size();
    pre7 = (pre7 + v * qpow(BASE, k, mod1e7)) % mod1e7;
    pre9 = (pre9 + v * qpow(BASE, k, mod1e9)) % mod1e9;
  }
  ll pre = pre7 * mod1e9 + pre9;
  ans += h[pre];
  h[pre]++;
}

矩阵运算

如果我们把相邻的相同字符一个看为正矩阵，一个看作逆矩阵，相乘就消除了。
因为，我们可以把奇数位置的字符全部当做正矩阵，偶数位置的字符当做负矩阵，然后进行矩阵运算，从而可以得到一个前缀矩阵。
与前缀HASH类似，相同的前缀矩阵的个数就是答案的个数。

复杂度：矩阵大小为 2，故复杂度为 O(2^3*n)

vector<Matrix> mat(M), rmat(M);
for (int i = 0; i < 26; i++) {
  Matrix& t = mat[i];
  t.Rand(); // 每个字符随机生成一个矩阵，并计算出逆矩阵
  while (!t.IsInv()) t.Rand();
  rmat[i] = t.Inv();
}
ll ans = 0;
Matrix pre(2);
pre.Union();
unordered_map<ll, ll> h;
h[pre.Hash()]++;
for (int i = 0; i < n; i++) {
  const char c = str[i];
  const ll v = c - 'a';
  pre = pre * (i & 1 ? mat[v] : rmat[v]);
  ull tmp = pre.Hash();
  ans += h[tmp];
  h[tmp]++;
}

总结，这道题可以使用next函数、前缀hash、前缀矩阵三种方法来做，其中 next函数最简单。

三、结构体（struct）

题意：给出 C++ 数据结构内存的对齐规则，然后告诉你一个符号求内存地址，以及一个地址求符号。

思路：超级大模拟。

首先需要读懂题，大概关键规则如下：

1）结构体的成员地址需要对齐的，对齐规则是之前成员的最大对齐长度。
2）如果一个成员是一个结构体，则对齐长度为最大的成员对齐长度（注意，不是成员的大小）。
3）对于一个类型，类型大小也需要按最带成员对齐长度进行对齐。

理解了上述三个规则后，就可以封装两个对象了。

成员对象：成员的类型、名字、在所示结构体的偏移量。

class Member {
 public:
  string type;
  string name;
  ll offset;
  Member(const string& type_ = "", const string& name_ = "", ll offset_ = 0)
      : type(type_), name(name_), offset(offset_) {}
};

结构体对象：类型大小、对齐大小、类名、成员列表、成员名字与索引的关系。
另外为了加速地址的查找，还需要储存每个成员的起始位置，用于二分快速定位到地址对应的成员。

struct Type {
 public:
  bool base_type;
  ll type_size;
  ll align_size;
  const std::string type_name;
  vector<Member> childs;
  std::unordered_map<string, ll> childName2Index;
  std::map<ll, ll> offset2Index;  // 储存成员的起始位置
  Type(const string& type_name_ = "", const ll type_size_ = 0,
       const bool base_type_ = false)
      : type_name(type_name_) {
    type_size = type_size_;
    align_size = type_size_;  // 默认对齐大小与类型大小一致
    base_type = base_type_;
  }
};

最后定义全局对象的关系表。

vector<Type> types;
unordered_map<string, ll> typeName2Index;

一开始初始化时，可以把基本类型都计算好，全局变量都当作一个全局结构体的成员。

vector<Type> types;
unordered_map<string, ll> typeName2Index;

Type* GetType(const string& name) {
  auto it = typeName2Index.find(name);
  if (it == typeName2Index.end()) return nullptr;
  return &types[it->second];
}

Type* AddType(const string& name, const ll type_size, const bool base_type) {
  types.push_back(Type(name, type_size, base_type));
  typeName2Index[name] = types.size() - 1;
  return &types.back();
}

const std::string kGlobal = "global";
void Init() {
  AddType("byte", 1, true);
  AddType("short", 2, true);
  AddType("int", 4, true);
  AddType("long", 8, true);
  AddType(kGlobal, 0, false);
}

题目有4个操作。

1）添加类型：添加新类型、依次添加成员并计算类内偏移量，最后计算类大小。
2）定义变量：等价于全局类型里添加成员。
3）名字找地址：查找在全局类型中的偏移量，一层层访问即可。

vector<string> names = ReadNames();
const Type* query_type = GetType(kGlobal);
ll query_offset = 0;
for (auto& name : names) {
  const Member* childMember = query_type->GetMember(name);
  query_offset += childMember->offset;
  query_type = GetType(childMember->type);
}
printf("%lld\n", query_offset);

4）地址找名字：在全局类型中，二分不断找到下个类型，一层层访问，最终找到叶子节点类型。

const Type* query_type = GetType(kGlobal);
string path;
while (true) {  // query_offset 已修正，代表 query_type 的偏移量
  auto it = query_type->offset2Index.upper_bound(query_offset);
  it--;                              //
  const ll childIndex = it->second;  // 如果 offset 很大，则指向最后一个
  const Member& member = query_type->childs[childIndex];
  const ll child_offset = member.offset;
  const std::string& child_name = member.name;
  const Type* child_type = GetType(member.type);
  query_offset -= child_offset;
  if (query_offset >= child_type->type_size) { 
    printf("ERR\n");  // 在空洞
    break;
  }
  path.append(child_name);
  query_type = child_type;
  if (query_type->base_type) {
    printf("%s\n", path.c_str());
    break;
  }
  path.push_back('.');
}

四、种树（tree）

题意：给一个有根树，从根开始，每天可以选一个节点种一棵树，每个节点的树种下之后每天会长一定高度，问最短需要多少天，所有节点的树的高度才能超过满足要求。
种树规则：父节点种树后，子节点才能种树。

思路：二分+数学公式

首先需要注意，树每天生长高度与哪天种的没关系，是从第一天计算的。

很容易想到，二分的做法，分为四个步骤。

1）二分答案。
2）不考虑父节点依赖的限制，计算出每个节点最晚需要在哪天种下
3）考虑父节点依赖限制，计算每个节点最晚需要在哪天种下。
4）拓扑排序，判断是否有答案。

二分答案

二分很经典，固定的写法。

ll l = n, r = 10e9 + 1;
while (l < r) {  // [l,r)
  ll mid = (l + r) / 2;
  if (Check(mid)) {
    r = mid;
  } else {
    l = mid + 1;
  }
}
printf("%lld\n", r);

无限制最晚天数

不考虑父节点限制，可以发现就是一个解方程问题。

方程分为三类：递增、常数、递减。
其中递减又分两种情况：答案在递减内与递减外。

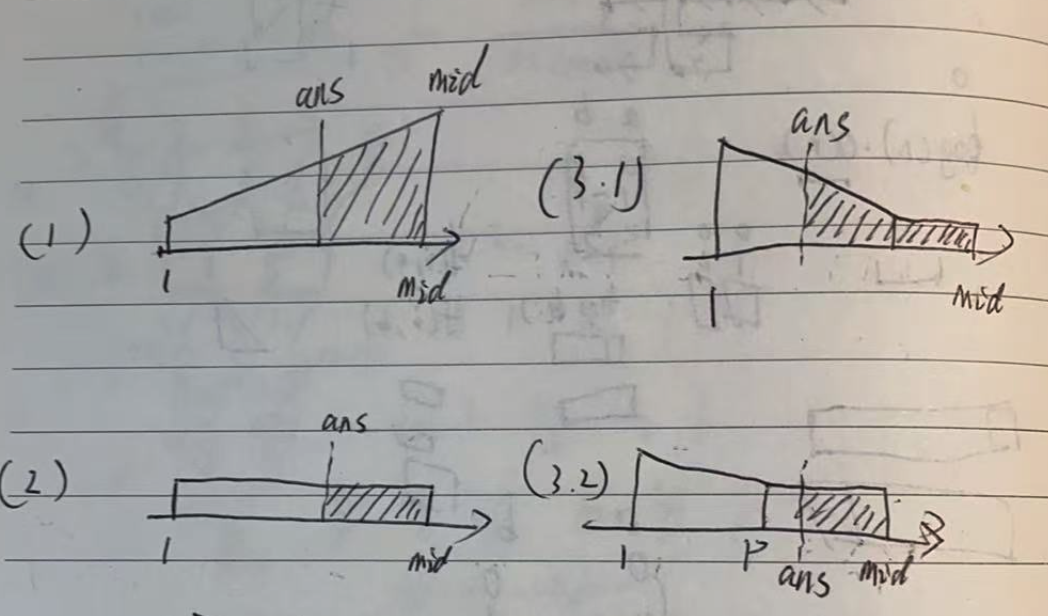
具体怎么解方程稍后再介绍。

// 计算每棵树最晚在哪天种植
for (ll i = 0; i < n; i++) {
  ll fastRet = CalFast(i, maxDay);
  lastDay[i] = fastRet;
  if (lastDay[i] == -1) {
    return false;
  }
}

考虑限制求最晚天数

由于父节点需要比子节点种的天数更早，所以父节点的天数需要小于子节点的天数。
依靠这个限制，可以更新父节点的最晚天数。

// 递归计算出树，修正 lastDay，父亲的 lastDay 需要小于儿子的
for (int i = 0; i < n; i++) {
  if (lastDay[i] < 1) return false;
  int pre = father[i];
  if (pre != -1) {
    lastDay[pre] = min(lastDay[pre], lastDay[i] - 1);
  }
}

拓扑排序判断答案

拓扑排序后，一个节点的最晚天数必须大于等于种树天数，才能满足要求。

sort(lastDay.begin(), lastDay.end());
// 判断答案
for (int i = 1; i <= n; i++) {
  if (lastDay[i - 1] < i) {
    return false;
  }
}
return true;

解方程

回到解方程这里，显然需要分类讨论。

递增时，如果有答案，直接解方程即可。

// (B+X*C + B+Y*C) * (Y - X + 1) / 2 >= A
// (2*B + Y*C + C*X) * (Y + 1 - X) >= 2*A
// (2*B + Y*C) * (Y + 1) - (2*B + Y*C) * X + C * (Y + 1) * X - C * X^2 >= 2*A
// (2*B + Y*C) * (Y + 1) + (C - 2 * B) * X - C * X^2 >= 2*A
// C * X^2 + (2*B - C) * X + 2*A - (2*B + Y*C) * (Y + 1) <= 0
// k = (C - 2 * B) / (2 * C) = 1 / 2 - B / C < 1
int128 AA = C;
int128 BB = 2 * B - C;
int128 CC = 2 * A - (2 * B + Y * C) * (Y + 1);
int128 X = (-BB + mySqrt(BB * BB - 4 * AA * CC)) / (2 * AA);  // 向下取整, X 更小
ret = X;

如果是常数，直接除法向上取整，求出答案。

ll minDay = (A + B - 1) / B;
if (minDay > maxDay) {
  return false;
}
ret = maxDay - minDay + 1;
return true;

如果是递减，需要分三种情况：枚举值在变成1之前、之后1就够了、之后1不够。

C = -C;
const ll oneDayBefor = (B - 1) / C;
if (oneDayBefor >= maxDay) {  // maxDay 在变成 1 之前
  return CheckDownDay(maxDay, A, B, C, ret);
} else {  // 变成 1 之后
  const ll oneDayNum = maxDay - oneDayBefor;
  if (oneDayNum >= A) {  // 使用 1 就够了
    ret = maxDay - A + 1;
    return true;
  } else {  // 1 不够
    return CheckDownDay(maxDay - oneDayNum, A - oneDayNum, B, C, ret);
  }
}

递减的解方程与递增的解方程类似，唯一的区别是，曲线的开口与递增相反，所以向下取整时可能不够，需要特殊判断一次。

int128 AA = C;
int128 BB = -(2 * B + C);
int128 CC = (2 * B - C * Y) * (Y + 1) - 2 * A;
int128 X = (-BB - mySqrt(BB * BB - 4 * AA * CC)) / (2 * AA);
// 如果不是整数解，答案会向下取整，需要减一位
if ((B - X * C + B - Y * C) * (Y - X + 1) / 2 < A) {
  X--;
}
ret = X;
return true;

二分代替解方程

解方程，公式比较复杂，还存在精度问题，容易出错。
其实可以通过二分求面积看是否满足要求，从而可以代替解方程。

五、最后

CSP-S 2023 这场比赛的每道题目不是很难，但是四道题合起来就算比较难了，而且代码量非常大。

第一题暴力枚举，算是签到题。
第二题就会把不少人卡主，动态规划是最简单的，字符串hash会冲突，矩阵运算则一般想不到。
第三题是一个很大的模拟题，考察面向对象封装能力，封装的好了，就不容易出BUG，否则调试到比赛结束。
第四题二分解方程，比赛的时候肯定会使用二分套二分，数据范围比较大，很容易超时。

《完》

-EOF-

本文公众号：天空的代码世界
个人微信号： tiankonguse
公众号 ID： tiankonguse-code

本文首发于公众号：天空的代码世界，微信号：tiankonguse
如果你想留言，可以在微信里面关注公众号进行留言。

比赛	A	B	C	D	题解
CSP-J 2024	扑克牌入门	地图探险普及−	小木棍普及/提高−	接龙提高+/省选−	题解
CSP-S 2024	决斗普及−	超速检测普及+/提高	染色提高+/省选−	擂台游戏 NOI/NOI+/CTSC	题解
CSP-J 2023	小苹果普及−	公路普及−	一元二次方程普及/提高−	旅游巴士普及+/提高	题解
CSP-S 2023	密码锁普及−	消消乐提高+/省选−	结构体提高+/省选−	种树提高+/省选−	题解