CCF CSP-S 2022 编程算法比赛

零、背景

最近我计划研究 CSP-J 与 CSP-S 的比赛题目，之前已经完成了 5 场比赛的题解，今天将分享 2022 年 CSP-S 第二轮比赛的详细题解。

A: BFS预处理+枚举优化
B: 区间极值查询(线段树/ST表)
C: 图上操作(惰性标记/哈希校验)
D: LCA+矩阵快速幂优化

代码地址： https://github.com/tiankonguse/leetcode-solutions/tree/master/other/CSP-S/

比赛题目分类与题解
CSP-J 2024 题解 A:扑克牌入门 B: 地图探险普及− C: 小木棍普及/提高− D: 接龙提高+/省选−
CSP-S 2024 题解 A:决斗普及− B: 超速检测普及+/提高 C: 染色提高+/省选− D: 擂台游戏 NOI/NOI+/CTSC
CSP-J 2023 题解 A:小苹果普及− B: 公路普及− C: 一元二次方程普及/提高− D: 旅游巴士普及+/提高
CSP-S 2023 题解 A:密码锁普及− B: 消消乐提高+/省选− C: 结构体提高+/省选− D: 种树提高+/省选−
CSP-J 2022 题解 A:乘方入门 B: 解密普及− C: 逻辑表达式普及+/提高 D: 上升点列普及/提高−
CSP-S 2022 题解 A:假期计划提高+/省选− B: 策略游戏普及+/提高 C: 星战省选/NOI− D: 数据传输省选/NOI−

一、假期计划

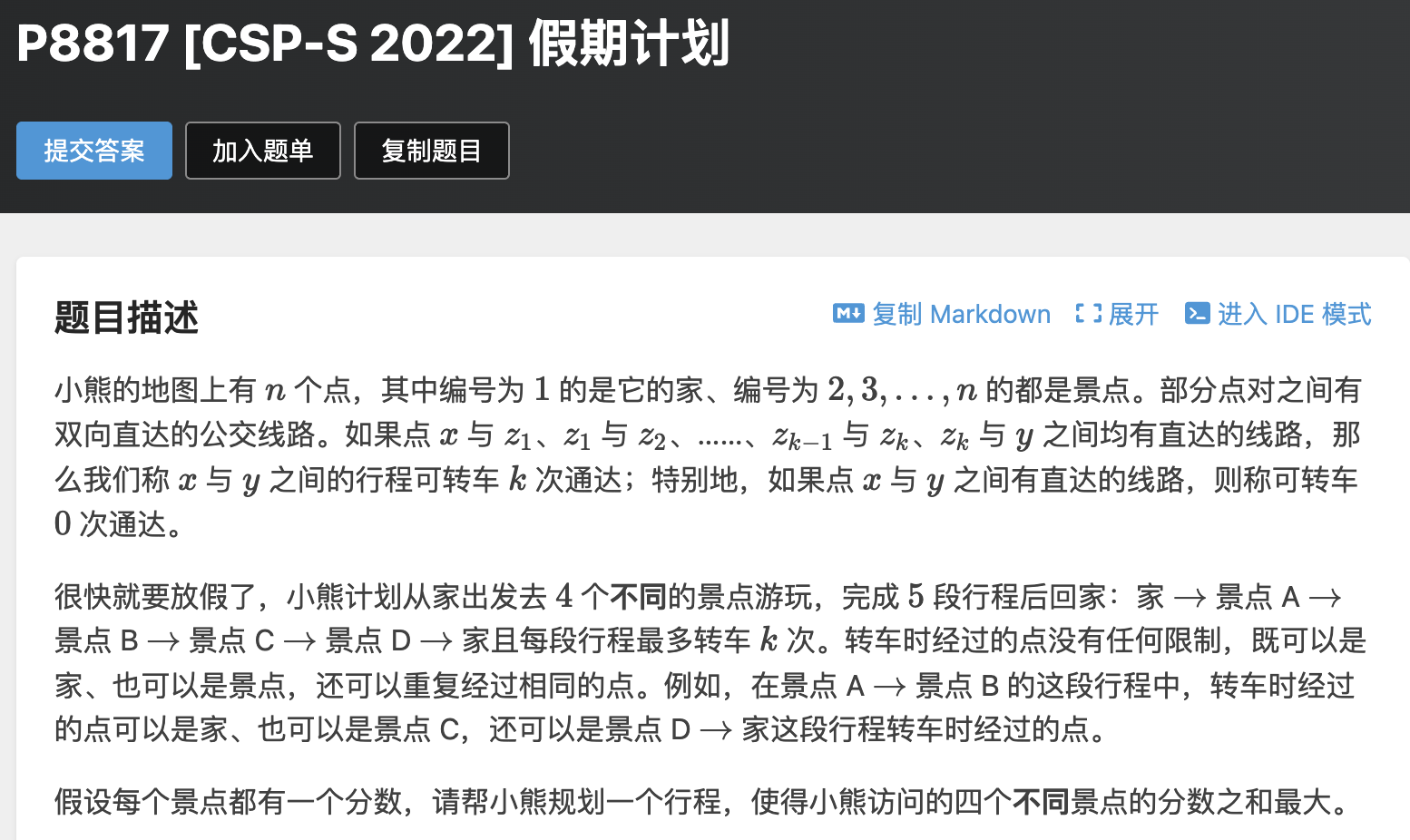
题意：给一个图，起点为 S，选四个不同的点A、B、C、D，组成一个路径S->A->B->C->D->S，要求每段路的距离不超过k，问怎么选择路径，才能使得四个点的得分和最大。

思路：BFS+枚举

K 很小只有 100，先 bfs 预处理出每个点可以达到哪些点，共需要预处理 n 次。
理论预处理复杂度：O(knm)
对于稀疏图，实际平均复杂度：O(kn)

for (int i = 1; i <= n; i++) {  // 以每个点为起点
  while (!que.empty()) que.pop();
  fill(vis.begin(), vis.end(), -1);
  que.push(i);
  vis[i] = 0;
  while (!que.empty()) {
    int u = que.front();
    que.pop();
    for (int v : g[u]) {
      if (vis[v] != -1) continue;
      vis[v] = vis[u] + 1;
      if (vis[v] > k + 1) continue;
      if (v == 1) {
        goOne[i] = 1;
      }
      G[i].push_back({scores[v], v});
      que.push(v);
    }
  }
  sort(G[i].begin(), G[i].end(), greater<>());
}

之后枚举路径(B->C),分别找到 B 节点和节点 C 可以到达S的相邻边。
显然，需要优先选择相邻边得分最大的那个顶点，可以预处理时对边排序从而直接查到。

for (int i = 2; i <= n; i++) {  // 以每个点为起点
  for (auto [c, v] : G[i]) {
    if (goOne[v] == 1) {
      GG[i].push_back({c, v});
    }
  }
}

B 顶点的相邻边里最大值可能是 C，故需枚举 TOP 2 的点，从而找到 A。
同理，C 顶点的相邻边里最大值和次大值可能是 B 和 A，故需枚举 TOP 3 的点。

简单起见，全部枚举 TOP 3 的点，求最大值即可。

// 路径结构：家 -> 景点 A -> 景点 B -> 景点 C -> 景点 D -> 家
// 优化策略：枚举中间两个景点 B 和 C
ll ans = 0;
for (int B = 2; B <= n; B++) {
  for (auto [score, C] : G[B]) {
    if (C == 1) continue;
    for (int i = 0; i < GG[B].size() && i < 3; i++) {  // 最多枚举前3个
      int A = GG[B][i].second;
      if (A == B || A == C) continue;
      for (int j = 0; j < GG[C].size() && j < 3; j++) { // 最多枚举前3个
        int D = GG[C][j].second;
        if (D == A || D == B || D == C) continue;
        ll tmp = scores[A] + scores[B] + scores[C] + scores[D];
        if (tmp > ans) {
          ans = tmp;
        }
      }
    }
  }
}
printf("%lld\n", ans);

二、策略游戏

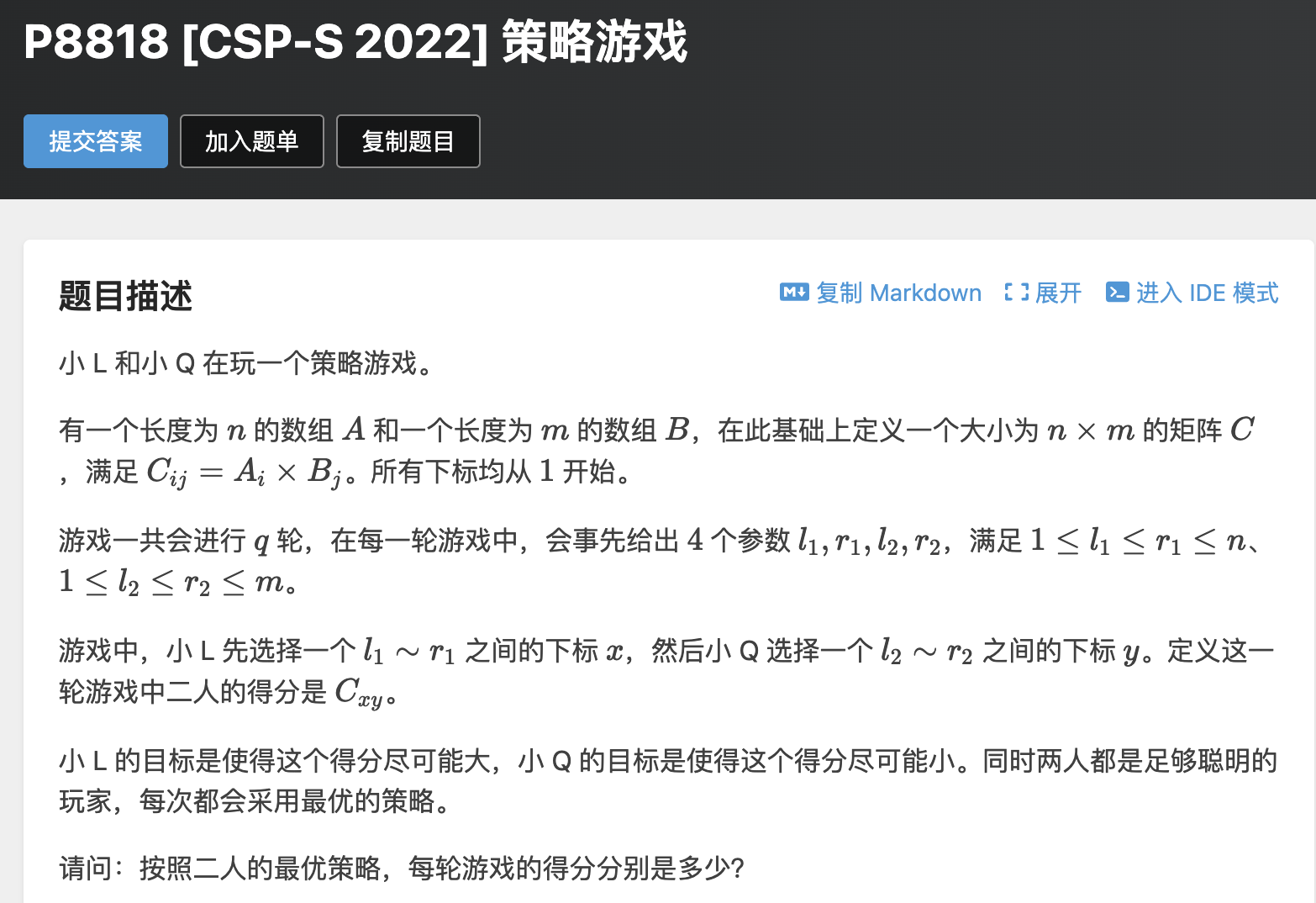
题意：给两个数组 A 和 B，每次询问时告诉两个数组的区间，问先在 A 区间里选择一个数字，再在 B 区间里选择一个数字，该怎么选择，才能使得选择的两个数字之积最大。
策略：A 区间目标是使结果最大，B 区间目标是使结果最小。

思路：区间最值，线段树或倍增

由于 B 区间后选择，所以 B 区间的策略对结果的影响更大。
例如 B 区间内有正数和负数，则 A 选正数时 B 选择负数，A 选负数时 B 选择正数，即不管 A 怎么选, B 都可以使得结果是负数。

根据上面的例子，可以推导出完整的策略。

情况一、B 区间有正有负
1.1）A 区间优先选择 0，答案为0。
1.2）A 只有正数，A选最小正数，此时B会选最小负数。
1.3）A 只有负数，A选最大负数，此时B会选最大正数。
1.4）A 区间有正数和负数，A选最小正数时B选最小负数，A选最大负数时B选最大整数，两者取最大值。

if (nodeB.posMax > 0 && nodeB.negMin < 0) {
  // 情况1：B 区间有正负，A 需要优先选择 0，其次正负都选择，取最小的
  if (nodeA.zero > 0) {
    ans = 0;
  } else if (nodeA.posMax > 0 && nodeA.negMin < 0) {
    ans = max(nodeA.posMin * nodeB.negMin, nodeA.negMax * nodeB.posMax);
  } else if (nodeA.posMax > 0) {
    ans = nodeA.posMin * nodeB.negMin;
  } else {
    ans = nodeA.negMax * nodeB.posMax;
  }
}

情况二、B 没有负数
2.1）A 有正数时选择最大正数，B 会优先选择 0，没有 0 时选择最小正数。
2.2）A 没正数有 0 时，选择 0
2.3）A 只有负数时，选择最大的负数，此时 B 会选择最大的正数。

if (nodeB.posMax > 0) {
  // 情况2：B 区间有正数没负数，A 需要优先选择正数，其次 0，取最大的负数
  if (nodeA.posMax > 0) {
    if (nodeB.zero > 0) {
      ans = 0;
    } else {
      ans = nodeA.posMax * nodeB.posMin;
    }
  } else if (nodeA.zero > 0) {
    ans = 0;
  } else {
    ans = nodeA.negMax * nodeB.posMax;
  }
}

情况三、B 没有正数。
与情况二相反，这里不再赘述。

情况四：两个都是 0，答案是0。

如何求区间的四个最值呢？
可以使用线段树进行区间查询，也可以使用倍增进行区间查询。

三、星战

题意：给一个图，四个操作，问每个操作后，图是否满足反攻条件。
操作1：删除一条边。
操作2：删除入度为 v 的所有边。
操作3：添加一条原始边。
操作4：添加入度为v的所有原始边。
反攻条件：每个顶点只有一个出度边，且每个顶点可以走到一个环上。

思路：惰性标记或者图上hash

可以证明，每个点出度为1时，必然可以实现反击, 且此时恰好剩余 n 条边。
故需要能够判断，每个点的出度是不是1。

按题意可以得到基本思路：针对四个操作，动态维护所有点的入度边集合与点的出度。

操作1：单边删除，O(1)更新总边数、点的出度
操作2：单点删除，需要删除多条边，O(1)计算总边数，O(n)计算点的出度
操作3：单边添加，O(1)更新总边数、点的出度
操作4：单点添加，需要添加多条边，O(1)计算总边数，O(n)计算出度

故暴力实现，复杂度O(n^2) 可以得 60 分。

惰性标记

操作2和操作4是批量操作，很容易想到线段树的区间更新。
不过这里是图，操作的点不是连续的区间。
不过可以借鉴区间操作的惰性标记思想。

所有操作O(1)实时计算总边数，只有总边数为 n 时，再进行批量操作的展开。

void DelAllInEdge(int v) {
  opList[opIndex] = -v;
  edgeNum -= inDeg[v];
  inDeg[v] = 0;
  lazyFlag[v] = opIndex; // 懒标记，记录最近一次批量操作
}
void AddAllInEdge(int v) {
  opList[opIndex] = v;
  edgeNum += inDegBase[v] - inDeg[v];
  inDeg[v] = inDegBase[v];
  lazyFlag[v] = opIndex; // 懒标记，记录最近一次批量操作
}

查询的时候，从前到后一次把积攒的批量操作展开。

void PushLazyFlag() {  //
  for (int i = prePushIndex + 1; i <= opIndex; i++) {
    int signVal = opList[i];
    int v = abs(signVal);
    if (v == 0) continue;            // 不是批量操作
    if (i != lazyFlag[v]) continue;  // 不是最后一个批量操作，不需要处理
    if (signVal > 0) {               // 全部添加
      for (auto it = rgDel[v].begin(); it != rgDel[v].end();) {
        auto tmpIt = it;
        it++;
        int u = tmpIt->first;
        MyAssert(rg[v].count(u) == 0);
        if (tmpIt->second > i) continue;  // 之后又删除
        realAddEdge(u, v);
      }
      lazyFlag[v] = 0;
    } else {
      for (auto it = rg[v].begin(); it != rg[v].end();) {
        auto tmpIt = it;
        it++;
        int u = tmpIt->first;
        MyAssert(rgDel[v].count(u) == 0);
        if (tmpIt->second > i) continue;  // 之后又添加的
        realDelEdge(u, v);
      }
      lazyFlag[v] = 0;
    }
  }
  prePushIndex = opIndex;
}

其实这个懒标记做法最坏情况下复杂度是O(nq)，不过图是一个稀疏图，实际可以得到 100 分。

图上hash

目标是检查每个点的出度是不是 1，维护一批点的出度成本很高。
如果能够虚拟出一个中间值，可以高效更新，且等价与出度为1的情况，则可以高效做这道题。

假设每个节点有一个特征值，每个边的特征值为入度顶点的特征值，则最终满足答案时，每个顶点一个出度，即边的累计特征值肯定等价于n个顶点的累计特征值。

累计特征值一般使用加法运算。
这样，通过维护出度顶点相邻边的和，即可得到剩余边的总和，进而代表出度顶点的总和。

单点更新如下：

void AddEdge(int u, int v) {
  inDeg[v]++;
  edgeNum++;
  inDegSum[v] = HashAdd(inDegSum[v], scores[u]);
  allScore = HashAdd(allScore, scores[u]);
}

批量添加如下：

void DelAllInEdge(int v) {
  edgeNum -= inDeg[v];
  inDeg[v] = 0;
  allScore = HashDel(allScore, inDegSum[v]);
  inDegSum[v] = 0;
}
void AddAllInEdge(int v) {
  edgeNum += inDegBase[v] - inDeg[v];
  inDeg[v] = inDegBase[v];
  allScore = HashAdd(allScore, HashDel(inDegSumBase[v], inDegSum[v]));
  inDegSum[v] = inDegSumBase[v];
}

最后只需要判断图剩余边的总和是否等于n个定点的和。

if (edgeNum == n && allScore == allScoreBase) {
  printf("YES\n");
} else {
  printf("NO\n");
}

当然，如果怕冲突，可以生成两套随机数，从而降低冲突的概率。
另外，这里使用异或代替和也是可以的。

四、数据传输

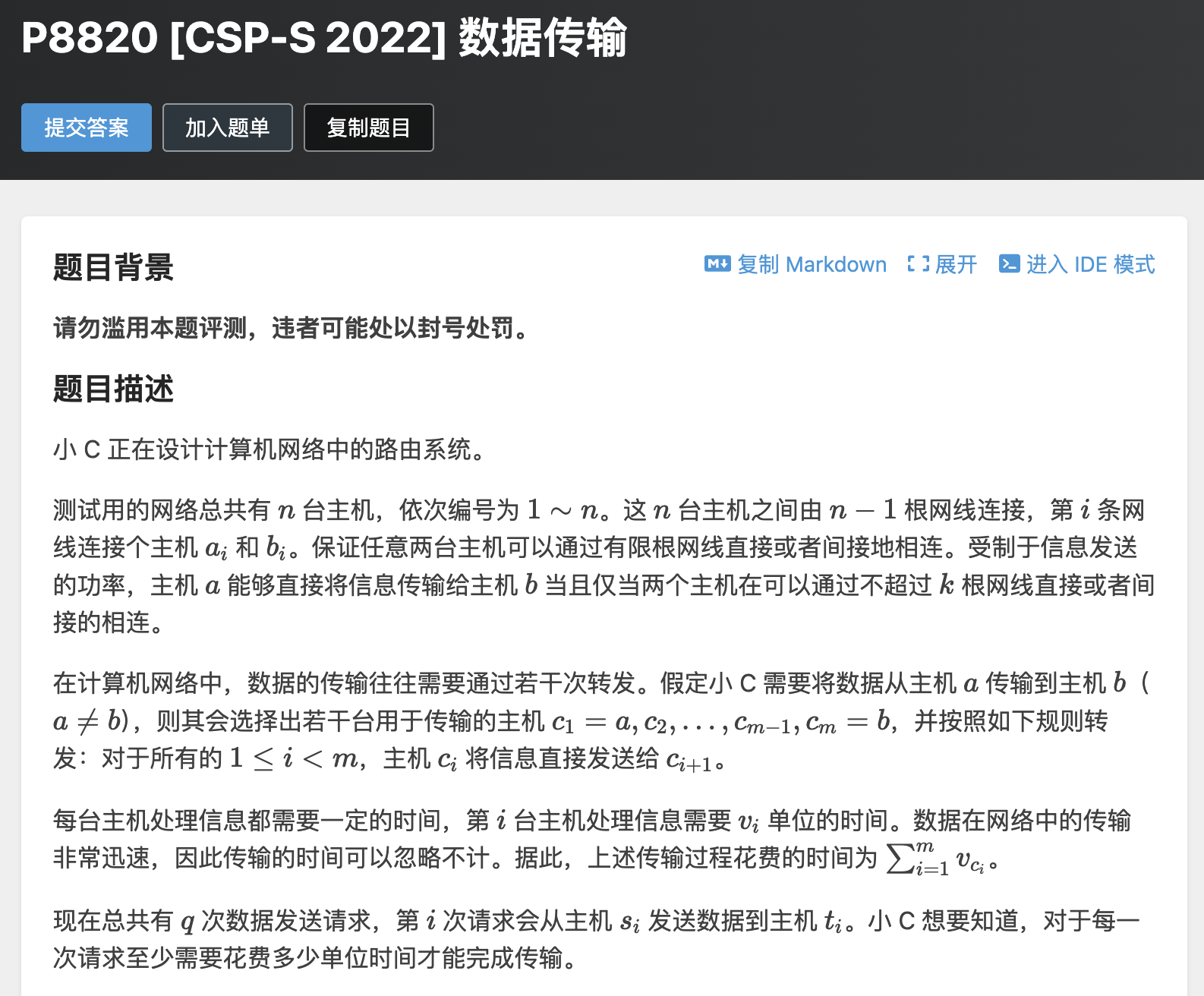
题意：给一个无向树，每次最多可以跳跃 k 个边，问从u到达点v经过的点的最小权重和。

思路：lca+图上矩阵倍增

如果 k 为 1，则是一个经典的路径和问题，lca 即可计算出来，此时可以得 16 分。

ll PathCostSum(int u, int v) {
  int lca = Lca(u, v);
  return preSum[u] + preSum[v] - 2 * preSum[lca] + costs[lca];
}

如果 k 为 2，则是经典的树上菲波那切数列，或者走楼梯，即走一步或者走两步。
答案最终分两种情况：一种是经过 lca，一种是答案不经过 kca，即在两边。

ll PathCostSum2(int u, int v) {
  if (dep[u] < dep[v]) {
    swap(u, v);  // 保障 u 是深度更深的, 即 v 可能是 lca
  }
  int lca = Lca(u, v);
  if (v == lca) {
    return costs[u] + PathCostPreKth2(u, dep[u] - dep[lca]);
  }
  // u -> lca -> v
  // u -> u_lca-1 -> v_lca-1, v
  ll ans1 = PathCostPreKth2(u, dep[u] - dep[lca]) + PathCostPreKth2(v, dep[v] - dep[lca]) - costs[lca];
  ll ans2 = PathCostPreKth2(u, dep[u] - dep[lca] - 1) + PathCostPreKth2(v, dep[v] - dep[lca] - 1);
  return min(ans1, ans2) + costs[u] + costs[v];
}

这时候有两种做法：迭代法或者矩阵幂。

我选择迭代法,即在倍增表里动态维护相邻的两个顶点的答案。

ll PathCostPreKth2(const int u, int k) {  //
  // u,u+1 -> u+2^i,u+1+2^i
  ll ans_l_1 = 0;
  ll ans_0 = 0;
  int u_0 = u;
  int u_l_1 = u;
  int firstFlag = true;
  for (int i = maxn_log - 1; k && i >= 0; i--) {
    if (k & (1 << i)) {
      ll tmp_ans_l_1 = min(ans_l_1 + F[u_l_1][i][K_0], ans_0 + F[u_0][i][K_L_1]);
      ll tmp_ans_0 = min(ans_0 + F[u_0][i][K_0], ans_l_1 + F[u_l_1][i][K_R_1]);
      ans_l_1 = tmp_ans_l_1;
      ans_0 = tmp_ans_0;
      u_0 = f[u_0][i][K_0];
      u_l_1 = f[u_l_1][i][K_0];
      k = k ^ (1 << i);
    }
  }
  return ans_0;
}

如果使用矩阵幂做，就需要构造出矩阵状态来。
此时，矩阵运算时各项相加取 max。

树上关系如下，两个点向上移动了一下。

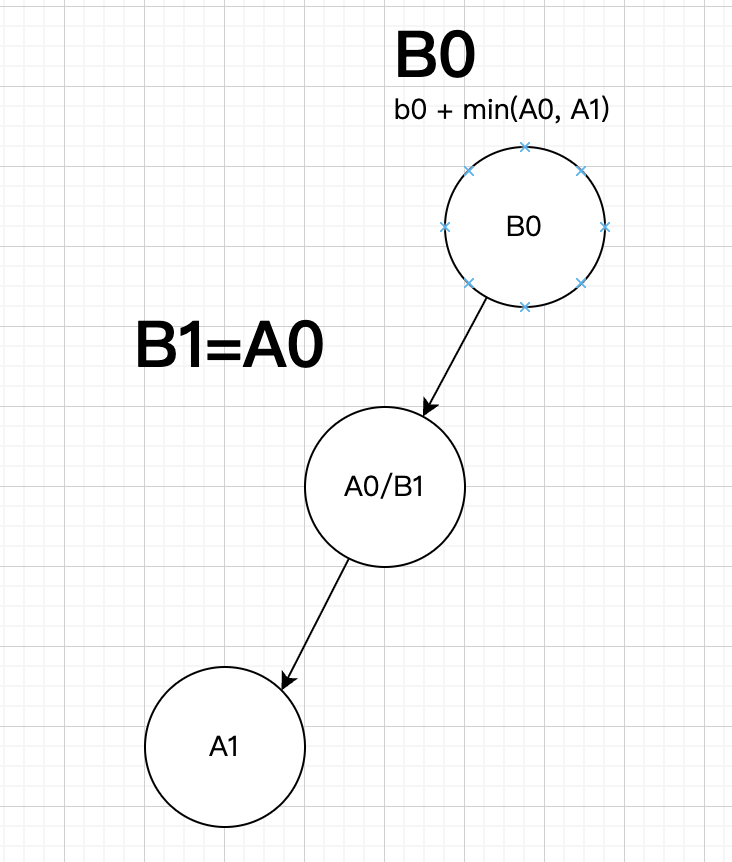
k 等于 2 的算法写出来之后，此时可以得 56 分

如果 k 为 3 时，基本思路是走一步、走两步、走三步。
此时会发现第四组样例无法通过。

原因是除了在路径上走，还可以走到非路径上，显然需要考虑每个节点相邻的最小权值节点。

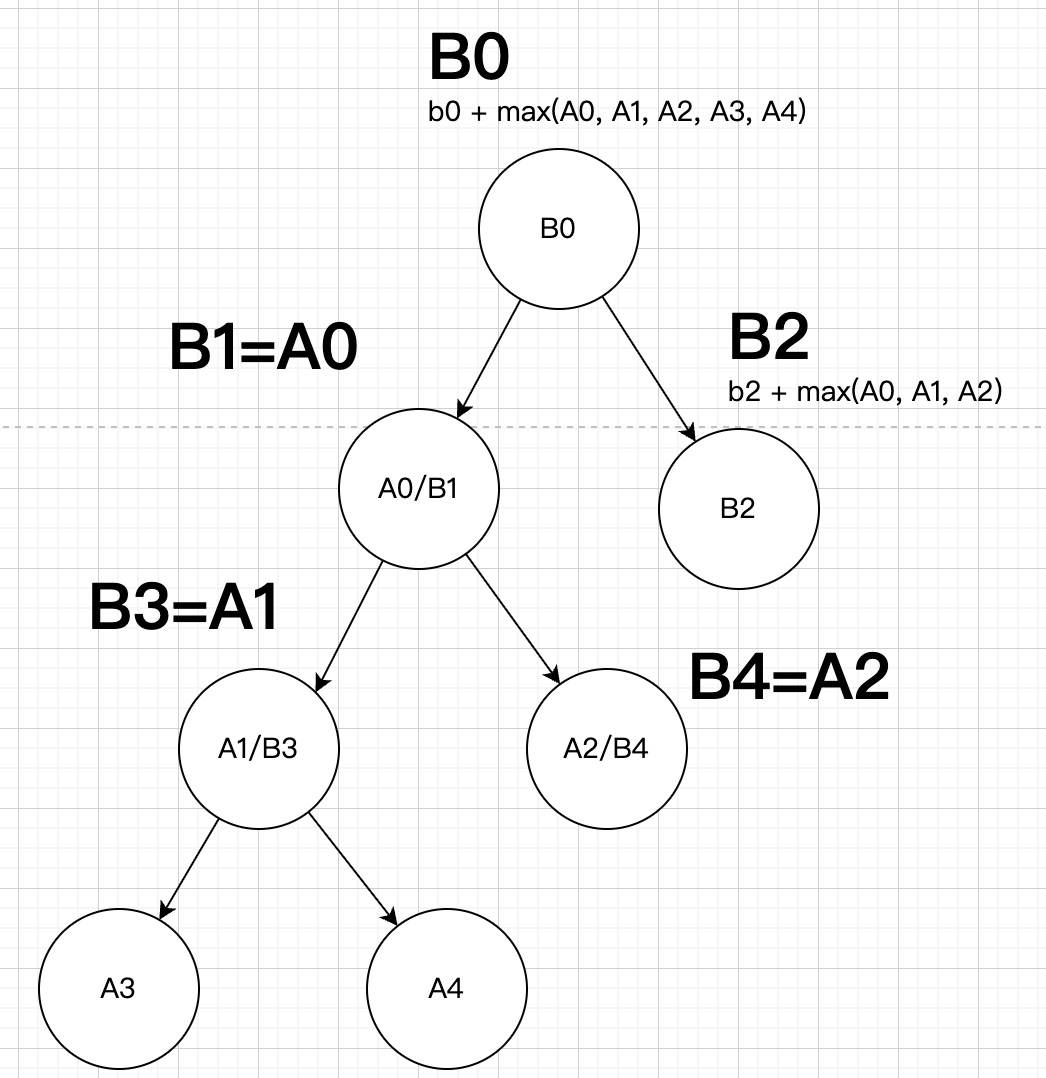
如上图，分析 B0，发现可以有 5 个点出发走 k 步到达，所以矩阵状态需要维护 5 个。
同样，计算分支状态 B1，需要三个状态转移得到。
而对于其他状态 B2、B3、B4，之前已经计算过了，直接赋值即可。

针对这个状态的计算公式，可以推导出矩阵状态。

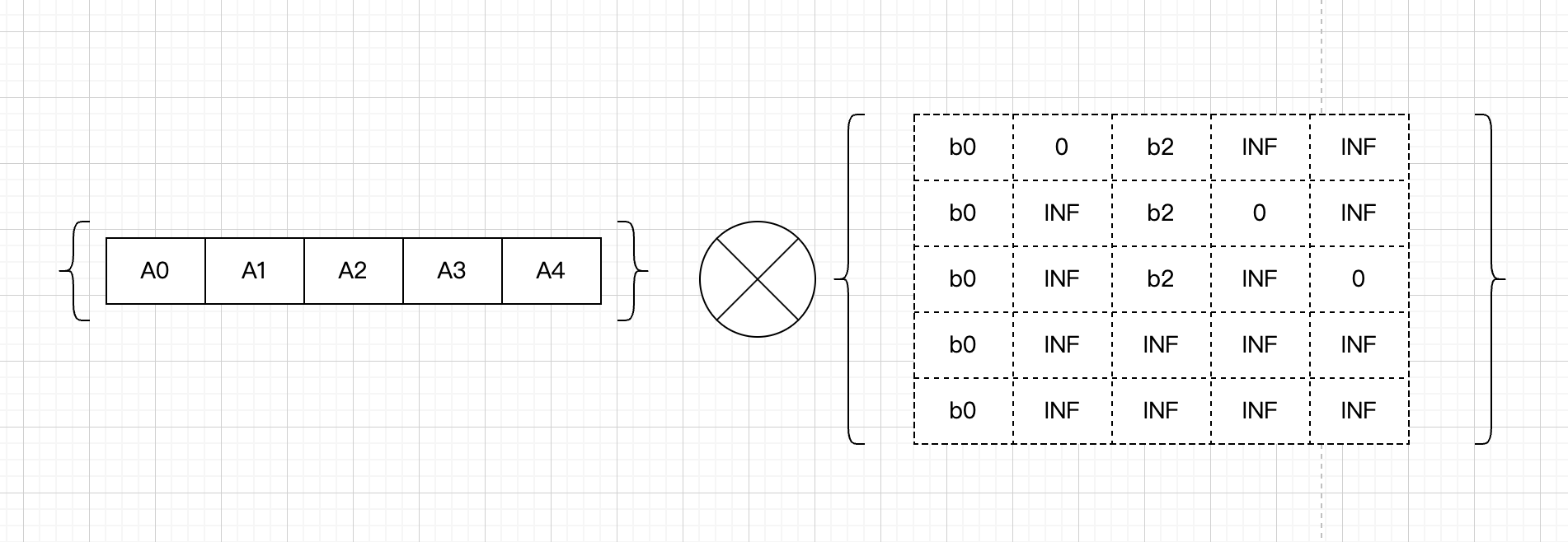
向上走一步的矩阵状态有了，就可以利用倍增，计算出走多步的状态。

类似于 K=2，合并答案时分多种情况。
两个路径分别得到 5 个状态，合并就是 25 个组合。
可以使用循环来判断两个状态是否可以一步到达。

for (int i = 0; i < kMatrixSize; i++) {
  for (int j = 0; j < kMatrixSize; j++) {
    int ii = (i + 1) / 2;
    int jj = (j + 1) / 2;
    if (ii + jj <= k) {  // 一步到位
      ans = min(ans, U.a[0][i] + V.a[0][j]);
    }
  }
}

另外，对于根节点和根节点的最值儿子，两个状态是重合的，需要减去重合值。

ans = min(ans, U.a[0][0] + V.a[0][0] - costs[lca]);  // 两个树根重合
if (k == 3) {  // 根的最小儿子重合
  ll tmpAns = U.a[0][2] + V.a[0][2] - minChild[lca];
  ans = min(ans, tmpAns);
}

注意事项：相邻的最小权值节点不仅仅是儿子，父节点也是，这一点我没注意到，调试了几个小时。

五、最后

这次比赛的后两题具有较高难度，考察了不常见的算法技巧：

第一题枚举中间两个点，难度还好。
第二题区间最值，难度也还好。
第三题批量操作很难处理，惰性标记可以水过去但是代码量很大。图上hash是最优写法。
第四题lca+图上矩阵倍增，我由于k=2选择迭代递推，k=3时递推时我只使用路径的3个状态，写到崩溃，最终调试发现是漏了相邻节点的情况。
写出来后样例也没通过，然后发现还有2个相邻最值儿子状态，改成矩阵运算后，还是没通过。
最后发现父节点也算相邻儿子。
算下来，第四题做了三天，注意事项非常多。

《完》

-EOF-

本文公众号：天空的代码世界
个人微信号：tiankonguse
公众号 ID：tiankonguse-code

本文首发于公众号：天空的代码世界，微信号：tiankonguse
如果你想留言，可以在微信里面关注公众号进行留言。