CSP-J 2020 编程算法比赛

零、背景

最近我计划研究 CSP-J 与 CSP-S 的比赛题目，之前已经完成了 8 场比赛的题解，今天将分享 2020 年 CSP-J 第二轮编程算法比赛的详细题解。

A: 二进制
B: 暴力统计、二分线段树、分块、计数平衡树(splay/树堆等)
C: 语法树，贪心
D: 动态规划

代码地址： https://github.com/tiankonguse/leetcode-solutions/tree/master/other/CSP-J/

比赛题目分类与题解
CSP-J 2024 题解 A:扑克牌入门 B: 地图探险普及− C: 小木棍普及/提高− D: 接龙提高+/省选−
CSP-S 2024 题解 A:决斗普及− B: 超速检测普及+/提高 C: 染色提高+/省选− D: 擂台游戏 NOI/NOI+/CTSC
CSP-J 2023 题解 A:小苹果普及− B: 公路普及− C: 一元二次方程普及/提高− D: 旅游巴士普及+/提高
CSP-S 2023 题解 A:密码锁普及− B: 消消乐提高+/省选− C: 结构体提高+/省选− D: 种树提高+/省选−
CSP-J 2022 题解 A:乘方入门 B: 解密普及− C: 逻辑表达式普及+/提高 D: 上升点列普及/提高−
CSP-S 2022 题解 A:假期计划提高+/省选− B: 策略游戏普及+/提高 C: 星战省选/NOI− D: 数据传输省选/NOI−
CSP-J 2021 题解 A:分糖果普及− B: 插入排序普及/提高− C: 网络连接普及/提高− D: 小熊的果篮普及+/提高
CSP-S 2021 题解 A:廊桥分配普及+/提高 B: 括号序列提高+/省选− C: 回文普及+/提高 D: 交通规划省选/NOI−
CSP-J 2020 题解 A:优秀的拆分入门 B: 直播获奖普及− C: 表达式普及+/提高 D: 方格取数普及+/提高

一、优秀的拆分

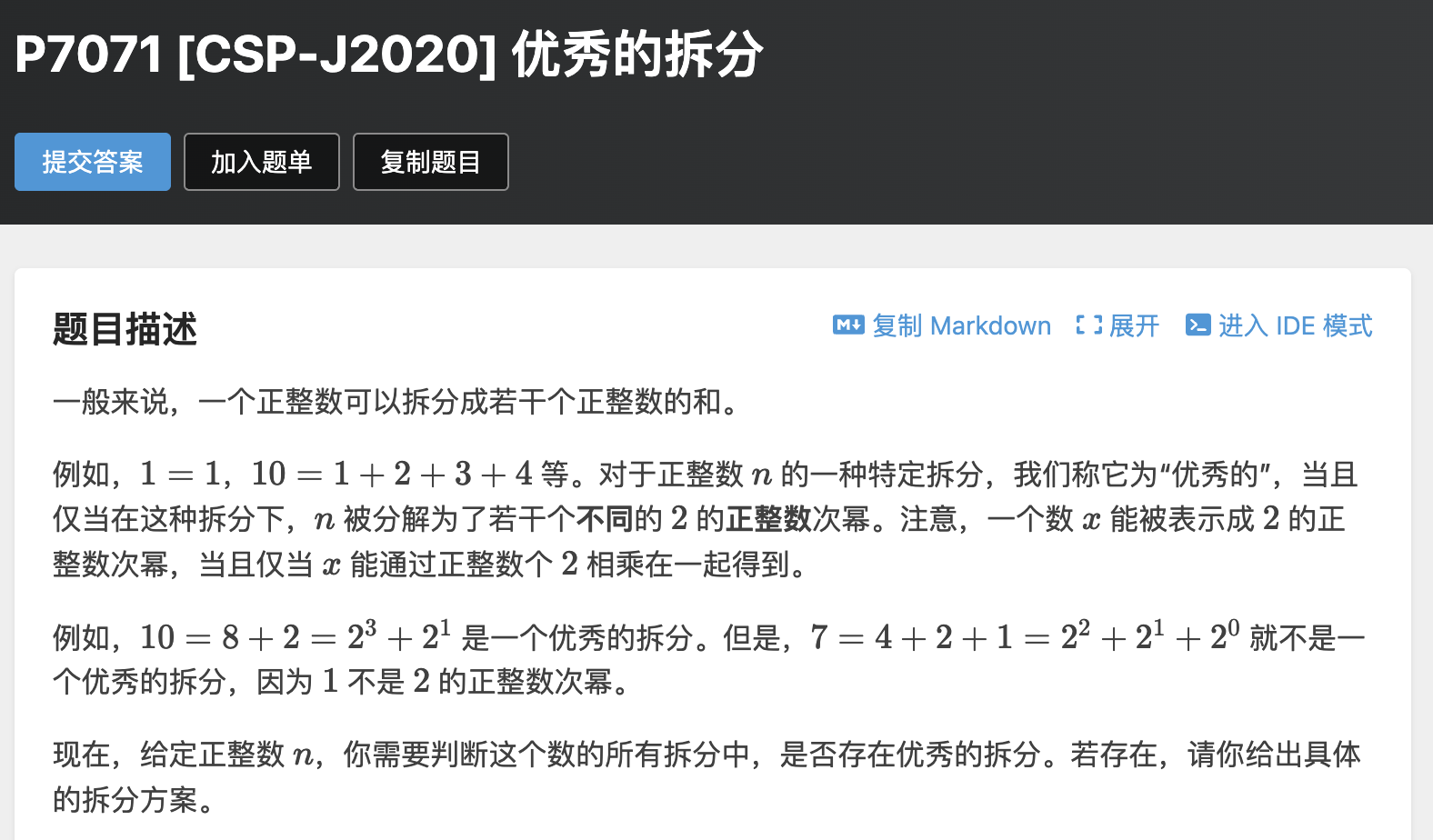
题意：给一个正整数，求将其拆分为若干个不同的2的幂之和。如果存在答案，从大到小输出。

思路：二进制

一个数拆分为2的不同幂之和，显然就是其二进制表示。
要求幂是正整数，因此奇数无法拆分。

if (n % 2 == 1) {
  printf("-1\n");
  return;
}
vector<int> nums;
int bit = 0;
while (n > 0) {
  if (n & 1) {
    nums.push_back(1 << bit);
  }
  bit++;
  n >>= 1;
}
std::reverse(nums.begin(), nums.end());

二、直播获奖

题意：比赛的前 w% 的选手获奖，现在依次告诉你一个选手的成绩，问目前获奖分数线是多少。

思路：统计

成绩的数据范围只有 600，最简单的方法是统计每个分数的人数，然后从大到小枚举分数，判断是否达到分数线。
复杂度：O(C*N)

vector<int> score(MaxScore + 1, 0);
for (int i = 1; i <= n; i++) {
  scanf("%d", &x);
  score[x]++;
  int rank = max(1, i * w / 100);
  int sum = 0;
  int ans = 0;
  for (int j = MaxScore; j >=0; j--) {
    sum += score[j];
    if (sum >= rank) {
      ans = j;
      break;
    }
  }
  printf("%d%c", ans, i == n ? '\n' : ' ');
}

优化：可以通过二分线段树来求分数线。
复杂度：O(N * log(C) log(C))

优化：分块，即对分数划分若干个块，每个块内分别计数，并计算块的和。
复杂度：O(N * sqrt(C))

优化：计数类平衡树，即维护一个支持重复节点的搜索树。
复杂度：O(N * log(C))

三、表达式

题意：给一个后缀逻辑运算表示，表达式的叶子节点都是已知值的变量，现在随机对一个变量的值取反，问表达式的值是多少。

思路：语法树与贪心

表达式本质上是一个二叉树，故需要定义树的节点。

enum { E_VAL = 0, E_AND, E_OR, E_NOT };
struct Node {
  int type;  //
  // int idx;
  int val;
  int left, right;
};

然后是节点分配器，通过下标来代替指针。

Node nodes[max6];
int nodeIdx = 0;

int NewNode(int type, int val = 0, int left = 0, int right = 0) {
  int idx = ++nodeIdx;
  nodes[idx].type = type;
  // nodes[idx].idx = idx;
  nodes[idx].val = val;
  nodes[idx].left = left;
  nodes[idx].right = right;
  return idx;
}

最后是通过栈，来构造表达式语法树。

stack<int> sta;
bool AddNode() {
  scanf("%s", buf);
  const char c = buf[0];
  if (c == 'x') {
    int idx = NewNode(E_VAL, 0);
    int name = ToInt(buf + 1);
    nameToIdx[name] = idx;
    idxToName[idx] = name;
    sta.push(idx);
  } else if (c == '|') {
    int rightIdx = sta.top();
    sta.pop();
    int leftIdx = sta.top();
    sta.pop();
    int idx = NewNode(E_OR, 0, leftIdx, rightIdx);
    sta.push(idx);
  } else if (c == '&') {
    int rightIdx = sta.top();
    sta.pop();
    int leftIdx = sta.top();
    sta.pop();
    int idx = NewNode(E_AND, 0, leftIdx, rightIdx);
    sta.push(idx);
  } else if (c == '!') {
    int leftIdx = sta.top();
    sta.pop();
    int idx = NewNode(E_NOT, 0, leftIdx, 0);
    sta.push(idx);
  } else {
    return false;
  }
  return true;
}
  while (AddNode()) {
    continue;
  }

  root = sta.top();

输入所有叶子节点变量的值后，就可以递归计算出表达式的值。

int DfsInit(int pre) {
  if (nodes[pre].type == E_AND) {
    int left = DfsInit(nodes[pre].left);
    int right = DfsInit(nodes[pre].right);
    return nodes[pre].val = left && right;
  } else if (nodes[pre].type == E_OR) {
    int left = DfsInit(nodes[pre].left);
    int right = DfsInit(nodes[pre].right);
    return nodes[pre].val = left || right;
  } else if (nodes[pre].type == E_NOT) {
    int left = DfsInit(nodes[pre].left);
    return nodes[pre].val = 1 - left;
  } else {
    return nodes[pre].val;
  }
}

如果暴力做这道题，复杂度是 O(q*n)。
分析叶子节点对结果的影响情况，会发现，要么不影响答案不变，要么影响答案取反。

什么时候不影响答案呢？
与或运算被短路的时候。
故可以递归预处理表达式树，将所有被短路的子树全部标记为不影响答案，剩余的就是影响答案的节点。

void DfsFlag(int pre, bool flag) {
  if (pre == 0) return;
  if (flag) { // 子树全部不影响答案
    if (nodes[pre].type == E_VAL) {
      ignoreIdxs[pre] = 1;
    }
    DfsFlag(nodes[pre].left, flag);
    DfsFlag(nodes[pre].right, flag);
    return;
  }

  if (nodes[pre].type == E_AND) {
    DfsFlag(nodes[pre].left, !RightVal(pre));
    DfsFlag(nodes[pre].right, !LeftVal(pre));
  } else if (nodes[pre].type == E_OR) {
    DfsFlag(nodes[pre].left, RightVal(pre));
    DfsFlag(nodes[pre].right, LeftVal(pre));
  } else if (nodes[pre].type == E_NOT) {
    DfsFlag(nodes[pre].left, false);
  } else {
    // do nothing
  }
}

预处理后，就可以O(1)处理询问了。

while (q--) {
  int name;
  scanf("%d", &name);
  int idx = nameToIdx[name];
  if (ignoreIdxs[idx]) {
    printf("%d\n", nodes[root].val);  // 这个位置变化不影响答案
  } else {
    printf("%d\n", 1 - nodes[root].val);  // 这个位置影响答案，即翻转
  }
}

四、方格取数

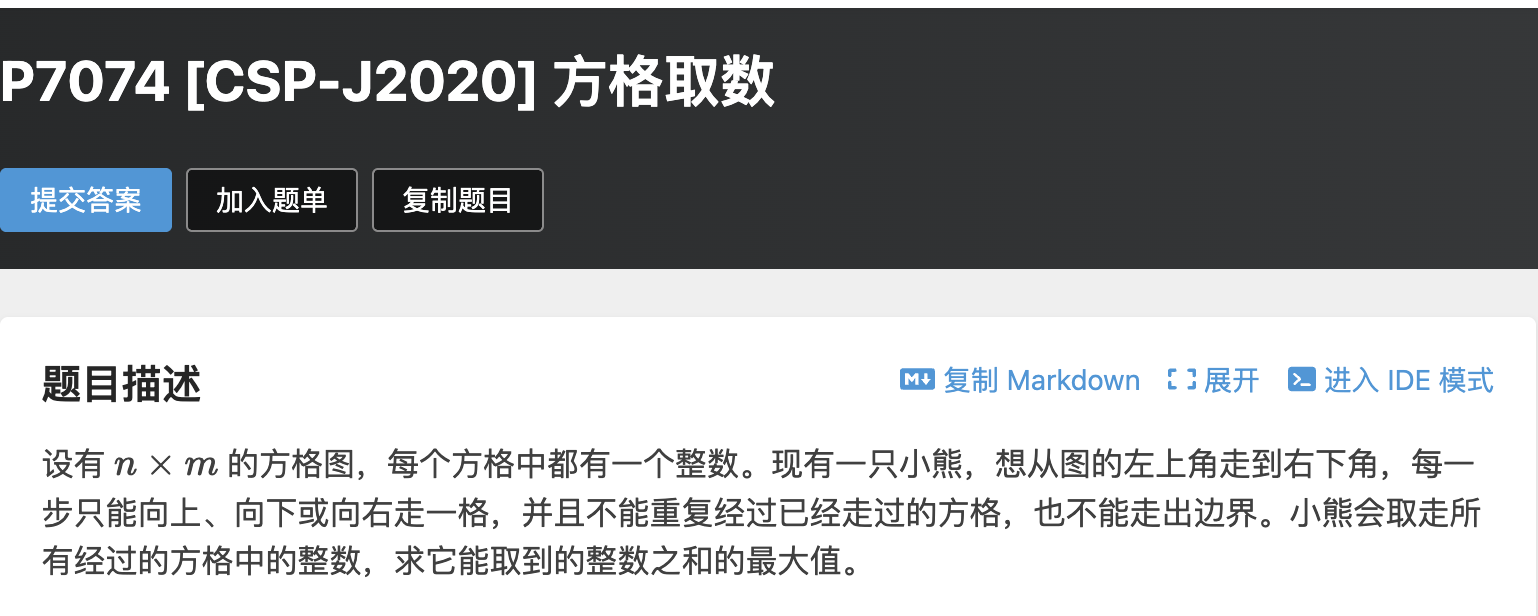
题意：给一个方格图，只能上下与向右走，同一个位置只能经过一次，问从左上角到达右下角的最大路径和。

思路：动态规划

只能从左向右，显然需要逐列处理，计算每一列的局部最优值。

状态定义:f(n,m) 从左上角到达位置(n,m)，下一步只能向右走时的最大路径和。

状态转移方程：当前列每个位置可以从上一列的任何一个位置到达。
其中 Dis(m,i,n) 含义为第 m 列从 i 到达 n 的线段和。

f(n,m) = max(f(i, m-1) + Dis(m, i, n));  

如果不做任何优化，复杂度是 O(n*m*n)，n 比较大时会超时。

将状态转移方程展开，如下

f(a,b) = max(
  f(0, b-1) + Dis(b, 0, a),
  f(1, b-1) + Dis(b, 1, a),
  f(2, b-1) + Dis(b, 2, a),
  ...
  f(a-1, b-1) + Dis(b, a-1, a),
  f(a, b-1) + Dis(b, a, a),
  f(a+1, b-1) + Dis(b, a, a+1),
  ...
  f(n-1, b-1) + Dis(b, a, n-1),
  f(n, b-1) + Dis(b, a, n),
);  

可以发现，状态转移方程分为两部分，第 a 行之上的是求上面路径的和，终点是 a，第 a 行之下的是求下面的路径之和，起点是 a。

上半部和下半部分开计算，令 f(a,b) = max(up(a,b), down(a,b))
然后可以发现，上半部可以复用相邻位置的信息。

up(a,b) = max(up(a-1,b), f(a, b-1)) + V;
down(a,b) = max(down(a+1, b), f(a.b-1)) + V;

故可以定义两个子状态，然后叠加求出父状态。
复杂度：O(n*m).

dp[0][1] = 0;
for (int i = 1; i <= n; i++) {
  dp[i][1] = a[i][1] + dp[i - 1][1];
}

for (int j = 2; j <= m; j++) {
  // 从上到下
  ll maxValue = -INFL;
  for (int i = 1; i <= n; i++) {
    maxValue = max(maxValue, dp[i][j - 1]) + a[i][j];
    dp[i][j] = max(dp[i][j], maxValue);
  }
  maxValue = ninf;
  for (int i = n; i >= 1; i--) {
    maxValue = max(maxValue, dp[i][j - 1]) + a[i][j];
    dp[i][j] = max(dp[i][j], maxValue);
  }
}
printf("%lld\n", dp[n][m]);

五、最后

这次比赛整体难度较低，第一题是二进制签到题，第二题暴力即可通过，第三题结合语法树与与或逻辑运算的短路特性，第四题是简单DP。

《完》

-EOF-

本文公众号：天空的代码世界
个人微信号：tiankonguse
公众号 ID：tiankonguse-code

本文首发于公众号：天空的代码世界，微信号：tiankonguse
如果你想留言，可以在微信里面关注公众号进行留言。