NOIP 2025 第二题 清仓甩卖 sale 题解

零、背景

之前已经在《NOIP 2025 pdf 题目分享》中分享了 NOIP 2025 的题目，也在《NOIP 2025 第一题 糖果店 candy 题解》里给出了第一题的题解。

这篇文章来分享 NOIP 2025 第二道题「清仓甩卖 sale」的题解。

PS：题目 pdf 和题解代码已上传网盘，公众号回复 NOIP-2025 获取。

一、题目

小 X 的糖果促销策略很成功，现在糖果店只剩下了 n 颗糖果，其中第 i (1 ≤ i ≤ n) 颗糖果的原价为 a_i 元。
小 X 计划将它们全部重新定价，清仓甩卖。
具体地，小 X 会将每颗糖果的清仓价格分别定为 1 元或 2 元。
设第 i (1 ≤ i ≤ n) 颗糖果的清仓价格为 w_i ∈ {1, 2} 元，则它的性价比被定义为原价与清仓价格的比值，即 a_i / w_i。

小 R 又带了 m 元钱买糖果。
这一次，小 R 希望他购买到的糖果的原价总和最大，于是他采用了以下购买策略：
将所有糖果按照性价比从大到小排序，然后依次考虑每一颗糖果。
具体地，若小 R 在考虑第 i (1 ≤ i ≤ n) 颗糖果时剩余的钱至少为 w_i 元，则他会购买这颗糖果，否则他会跳过这颗糖果，继续考虑下一颗。
特别地，若存在两颗糖果的性价比相同，则小 R 会先考虑原价较高的糖果；
若存在两颗糖果的性价比与原价均相同，则小 R 会先考虑编号较小的糖果。

例如，若小 X 的糖果商店剩余 3 颗糖果，原价分别为 a_1 = 1、a_2 = 3、a_3 = 5，而清仓价格分别为 w_1 = w_2 = 1、w_3 = 2，则性价比分别为 1、3、5/2。
因此小 R 会先考虑第 2 颗糖果，然后考虑第 3 颗糖果，最后考虑第 1 颗糖果。

小 R 想知道，在小 X 的所有 2^n 种定价方案中，有多少种定价方案使得他按照上述购买策略能购买到的糖果的原价总和最大。
你需要帮助小 R 求出满足要求的定价方案的数量。
由于答案可能较大，你只需要求出答案对 998,244,353 取模后的结果。

二、题意分析

我们先来分析购买策略。
对于给定的一组清仓价格组合，按照题目中的规则，购买顺序以及最终买到的糖果集合（原价总和）都是唯一确定的。
但是，这个策略并不一定总是得到全局最优解：有些定价方案下，按照这个策略买到的原价总和会比真正的最优方案更小。

如果先不看题目给出的购买顺序，只考虑有 m 元钱、每颗糖果价格为 w_i、价值为 a_i，那就是一个标准的 0-1 背包问题：求能得到的最大原价总和。
这不就是最基本的背包问题吗？

在这个背包模型下，只要还能买得起当前糖果，继续买性价比最高的糖果本身没有问题。
真正导致不最优的情况，是当当前糖果价格为 2 元而手上只剩下 1 元时：这时会跳过一些性价比更高的糖果，改去买后面性价比较低但只要 1 元的糖果。

具体来说，一种典型的“坏”情况是：
前面买了一个 1 元的糖果，原价记为 x。
后面遇到一个没钱买的 2 元糖果，原价记为 y。
再往后只能买 1 元的糖果，这部分买到的总原价记为 z。

当 y > x + z 时，说明这个 2 元糖果的性价比更高，按照题目策略做出的选择并不是全局最优。
因此，我们可以把所有定价方案分成两类：购买策略是最优的“好”方案，以及存在这种“坏”情况的“坏”方案。
题目要我们求的是好方案的数量。
直接统计好方案不容易，不如先算出总方案数 2^n，再减去所有“坏”方案的数量。

继续分析上面的不等式 y > x + z，可以从购买顺序中抽象出几个关键的位置 X、Y、Z，帮助我们系统地统计所有“坏”方案。

下面的讨论中，约定在性价比从大到小的顺序里：X/1 表示“最后一个被买到的 1 元糖果”，Y/2 表示“紧挨在 X/1 之后但没有被买到的 2 元糖果”，Z/1 表示“在 Y/2 之后、最后一个被买到的 1 元糖果”（如果存在）。

性质1：在性价比列表中，X/1 之前的糖果都会被购买。
因此可以给 X 下一个定义：X 是性价比列表中连续购买的糖果里最后一个糖果的位置。

如下图，由于在选择 X/1 之后还剩余 1 元钱，说明在 X/1 之前至少还能支付 2 元，所以这些糖果肯定都会被购买。

性质2：(Z,X) 之间的价格都是 2。

根据购买策略，先用 1 元钱购买了 X，剩余 1 元钱。
然后遇到价格为 2 元的 Y 买不起，直到 Z 才把这 1 元钱花出去。
这说明在性价比列表中，Z 与 X 之间的糖果价格都是 2，不可能是 1。

反证法：如果中间存在价格为 1 的糖果，那么性价比更高，就会优先购买它，而不会最后才购买 Z。

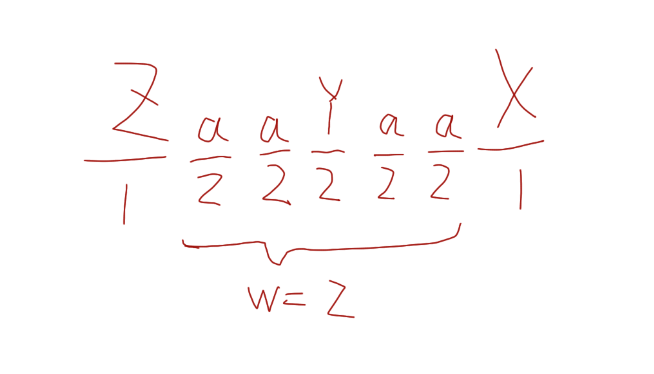
性质3：X 挨着 Y/2。

反证法：假设 Y/2 与 X/1 之间还有一个 YY/2。
则 YY/2 肯定也没买。
由于 YY/2 的性价比大于等于 Y/2，所以对应的原价 YY 也满足 YY > x + z。
此时，YY 就会变成新的 Y。

这个过程可以递归进行，最终可以推导出 Y/2 一定是紧挨着 X/1 的。

此时给 Y 下一个定义：
Y/2 为性价比列表中，小于 X/1 的第一个糖果。

性质4：在按原价排序的列表中，Y 之前的糖果都购买了。

如下图，由于 Y/2 与 X 是挨着的，所以在性价比列表中，不管 Y 之前的价格是多少，这些糖果肯定都在 X 之前被考虑。
因此，在原价列表中，Y 之前的糖果肯定都购买了。

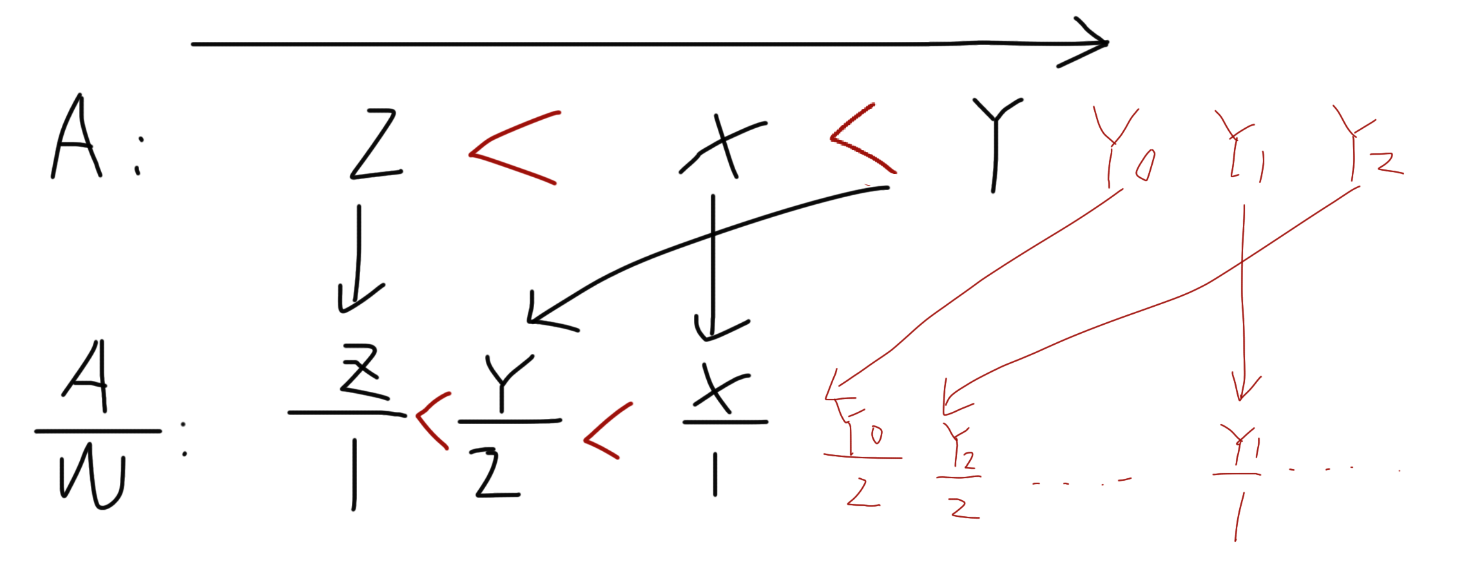
性质5：所有非最优组合，都有唯一的一对 X/1 和 Y/2。

根据 X 和 Y 的定义，这两个位置是唯一确定的。
因此，每种非最优组合，都可以用对应的一对 X/1 和 Y/2 来表示。

这样这道题的解法也就出来了：
通过枚举 X/1 和 Y/2 的所有情况，然后计算出符合这种组合的方案数。

三、算法分析

实现时，我们会把所有原价 a_i 按从小到大排序成数组 A，并用下标 x、y、z 来对应上文中的位置 X、Y、Z。
对于固定的一对 X 和 Y，什么时候对应的组合不是最优的呢？

根据非最优的条件 Y > X + Z，可以推导出 Y 一定大于 X。

// 不满足 y > x + z
if (A[y] == A[x]) continue;  

另外根据 Y/2 < X，也可以推导出 Y < 2 * X。

// 一旦不满足，后续的都不满足
if (A[y] >= 2 * A[x]) break;  

根据性质 4，Y 之前的糖果都购买了，预算至少要满足 m >= n - y。
再考虑 X 占用 1 元钱、Z 占用 1 元钱，更精确的条件是 m - 2 >= n - y。

// [y+1, n] 需要全选，价格最低为 1，至少需要 n-y 元
if (m - 2 < n - y) continue;  

当这三个条件都满足后，就可以进一步确定哪些位置是必选、哪些位置是可选的。

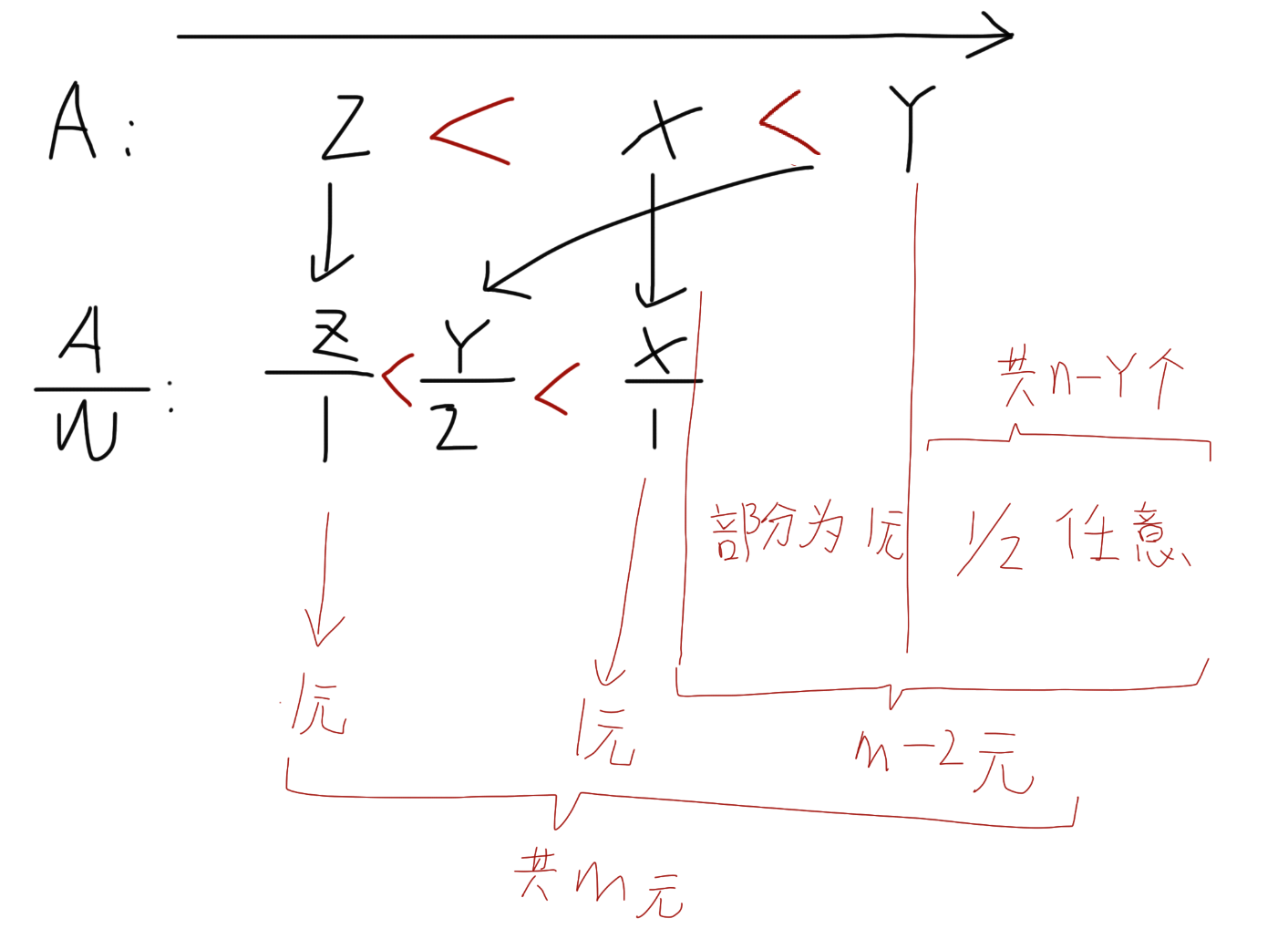
如上图：
大于 Y 的有 n-y 个，可以选择购买 1 元或者 2 元。
先假设它们都至少花 1 元买下，则会用掉 n-y 元，还剩余 (m-2) - (n-y) 元。
这时，这 n-y 个糖果相当于变成了“要么再多加 1 元变成价格 2，要么不加只用 1 元买”的选择。

[X+1,Y-1] 之间的糖果也有一部分可以选择购买 1 元，共有 (Y-1) - (X+1) + 1 = Y - X - 1 个位置。
把这段和后面大于 Y 的部分合并，一共是 (n - y) + (y - x - 1) 个位置，从中选择 (m - 2) - (n - y) 个位置设置为 1 元购买。

const ll leftOne = (m - 2) - (n - y);
const ll tmp = C((n - y) + (y - x - 1), leftOne);

根据性质2：(Z,X) 之间的价格都是 2。
这个性质可以推导出 (Z,X) 之间糖果的价格是确定的，再往前 [1,Z] 的价格则无所谓了，因为已经不是最优解了。
所以，[1,Z] 之间的糖果，可以任意设置1元或者2元，共有 2^Z 种情况。

const ll tmpAns = tmp * pow2[z] % mod;

Z 的价格也可以是 2，当 [1,Z] 的价格全都是 2 时，相当于还有 1 元钱没有花出去，依旧不是最优解。
由此可以得出结论：只要找到满足 Y > X + Z 的最大 Z，它后面任意的 1 元或者 2 元， 都对应着一类“坏”方案。

Y 和 Z 确定后，如何找到最大的 Z 呢？
正常情况下，需要 O(n) 的扫描遍历才能确定每对 (X,Y) 对应的最大 Z，再加上枚举 X 和 Y，总复杂度就是 O(n^3)。

可以发现，当 X 固定时，Y 与 Z 的关系是正相关的。
所以，可以使用双指针来边遍历 Y 边计算 Z 即可。

while (z < n && A[z + 1] + A[x] < A[y]) {
  z++;
}

四、代码实现

首先需要预处理出组合数 C(n,m) 与 pow2[n]。
这里我使用逆元进行计算组合数。

void Init() {
  pow2.resize(max4);
  pow2[0] = 1;
  for (int i = 1; i < max4; i++) {
    pow2[i] = (pow2[i - 1] * 2) % mod;
  }

  P.resize(max4);
  P[0] = 1;

  for (int i = 1; i < max4; i++) {
    P[i] = (P[i - 1] * i) % mod;
  }

  RP.resize(max4);
  for (int i = 0; i < max4; i++) {
    RP[i] = inv(P[i], mod);
  }
}
inline ll C(ll n, ll r) {
  //   return CC[n][r];
  if (n < r) return 0;
  ll Anr = P[n] * RP[n - r] % mod;
  return Anr * RP[r] % mod;
}

然后就是两层循环，外层遍历 X，内层遍历 Y，计算答案。

ll Solver(vector<ll>& A, const ll n, const ll m) {
  sort(A.begin(), A.end());
  // A: 1  ... z    ...  x    ... y     ...  n
  // B:    ... z(1) ...  y(2) ... x(1)  ...
  //  y > x + z
  //  y < 2 * x
  //  [y+1, n] 不管是 1 还是 2，都肯定会选择, 共 n-y 个
  //  y 的价钱是 2，没有选择
  //  [x+1,y-1] 只有价钱是 1 时才能选择，共 y-x-1 个
  //  x 的价钱是 1，选择的倒数第二个 1，剩余 1 元
  //  [z+1, x-1] 之间的价格都是 2，无法选择
  //  z 的价钱是 1，最后一个 1，剩余 0 元，有可能不存在
  ll ans = pow2[n];
  //   if (m == 1) {
  //     return ans;
  //   }
  for (int x = 1; x <= n; x++) {
    int z = 0;
    for (int y = x + 1; y <= n; y++) {
      if (A[y] == A[x]) continue;   // 不满足 y > x + z
      if (m - 2 < n - y) continue;  // [y+1, n] 需要全选，价格最低为 1，至少需要 n-y 元
      if (A[y] >= 2 * A[x]) break;  // 不满足 A[y] < 2 * A[x], 后续的都不满足
      // 找到最大的 z， 满足 A[z] + A[x] < A[y], 可以不选，即包括 z
      while (z < n && A[z + 1] + A[x] < A[y]) {
        z++;
      }
      // 已经构造出反例 A[z] + A[x] < A[y]，[1,z] 这些位置的价格可以是 1 也可以是 2，共 2^z 种情况
      // [y+1, n] 先至少选择一个，剩余 (m-2) - (n-y) 元钱，共有 (n - y) + (y - x - 1) 个位置共选择
      const ll leftOne = (m - 2) - (n - y);
      const ll tmp = C((n - y) + (y - x - 1), leftOne) * pow2[z] % mod;
      ans = (ans - tmp + mod) % mod;
    }
  }

  return ans;
}

五、总结

总结一下，这道题的关键在于：先从购买策略中抽象出“坏”方案的特征，然后把这些“坏”方案的数量用组合数精确地统计出来，最后用总方案数减去“坏”方案数得到答案。

另外，注意 n 最大是 5*10^3、m 最大是 2n-1 即大概是 10^4，预处理组合数和阶乘的时候，数组要开得足够大，避免越界或溢出。

《完》

-EOF-

本文公众号：天空的代码世界
个人微信号：tiankonguse
公众号 ID：tiankonguse-code