NOIP 2025 第四题 序列询问 query 单调队列题解

零、背景

之前已经在《pdf 题目分享》中分享了 NOIP 2025 的题目，在《糖果店 candy 题解》里给出了第一题的题解，在《清仓甩卖 sale 题解》给出了第二题的题解。

这篇文章来分享 NOIP 2025 第四道题「序列询问 query」的单调队列角度的题解。

PS：题目 pdf、官网测试数据、题解代码已上传网盘，公众号回复 NOIP-2025 获取。
PS2：最近工作上比较忙，所以更新会比较慢，见谅。

一、题目

给定一个长度为 n 的整数序列 a1, a2, . . . , an。
有 q 次询问，其中第 j 次询问将会给出 [L, R]。
定义区间 [l, r] 是极好的，当且仅当区间 [l, r] 的长度在 [L,R] 内。
定义区间 [l, r] 的权值为 S(l,r) = sum(a[l],...,a[r])。
对于所有 i = 1, 2, . . . , n，求出所有包含 i 的极好区间的最大权值，即 max(S(l,r)), l <= i <= r。

对于每次询问，设包含 i 的极好区间的最大权值为 ki，输出一行一个非负整数，表示 XOR((ki * i) % 2^64)。
其中 XOR 表示二进制按位异或。
注意：对于任意整数 x，存在唯一的非负整数 y 满足 y ≡ x (mod 2^64)。

二、题意分析

首先是理解题意。
对于每个位置 i，需要找到覆盖 i 的最大权值的极好区间。

那覆盖 i 的极好区间有哪些呢？

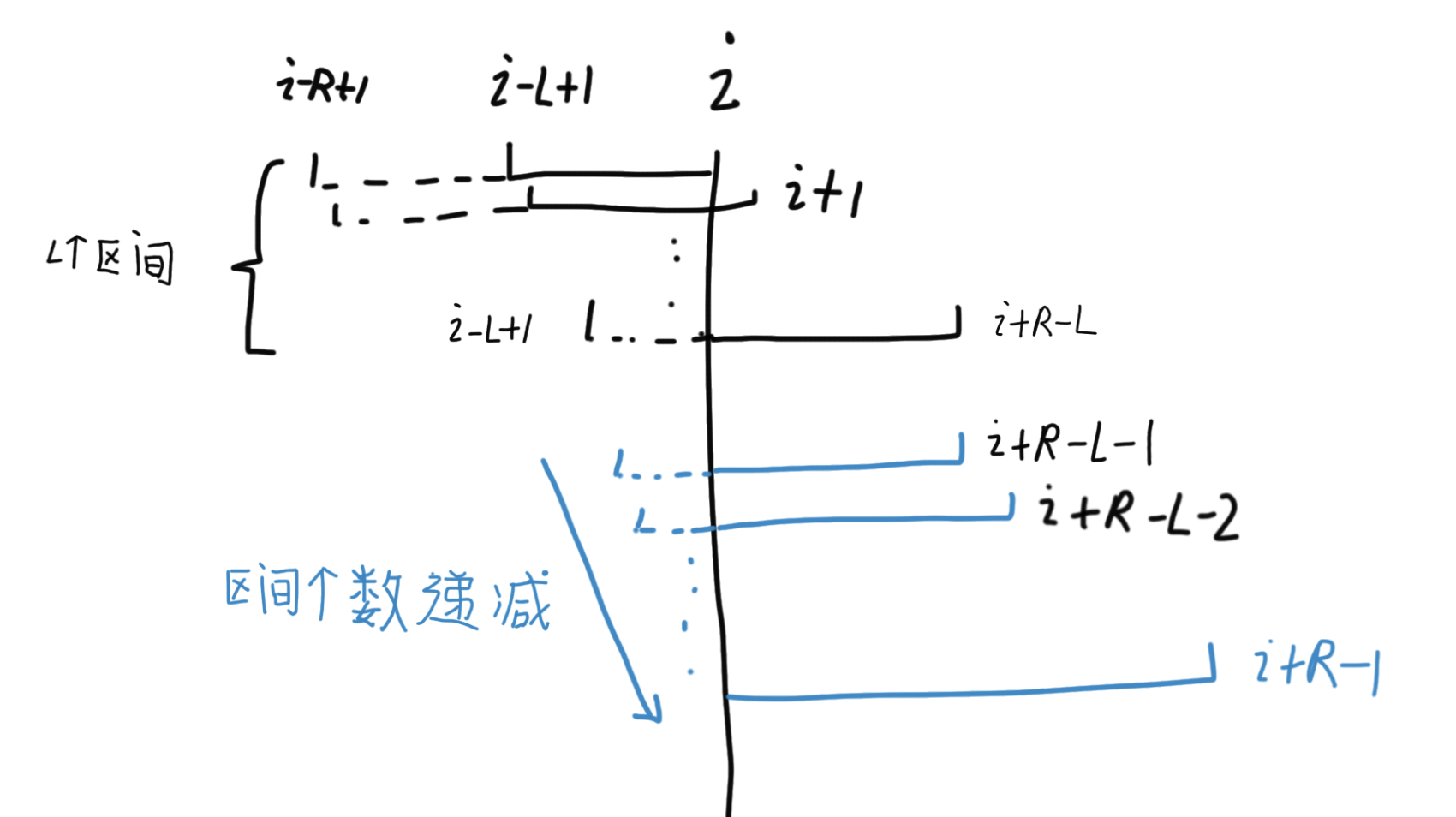
如上图，可以根据区间的右边界来进行划分分组。
以 [i,i+R-L] 为右边界时，长度为 [L,R]的极好区间都是存在的，即都有 R-L+1个极好区间。
i+R-L 是一个分界线，再往右，长度最短为 L 的极好区间就不存在了，即极好区间个数减一个。
再往右，每右移一位，极好区间的最短长度就加一，极好区间个数就减一。

这个覆盖 i 的极好区间的分布特征如下，分为两段，第一段是满的，第二段递减。

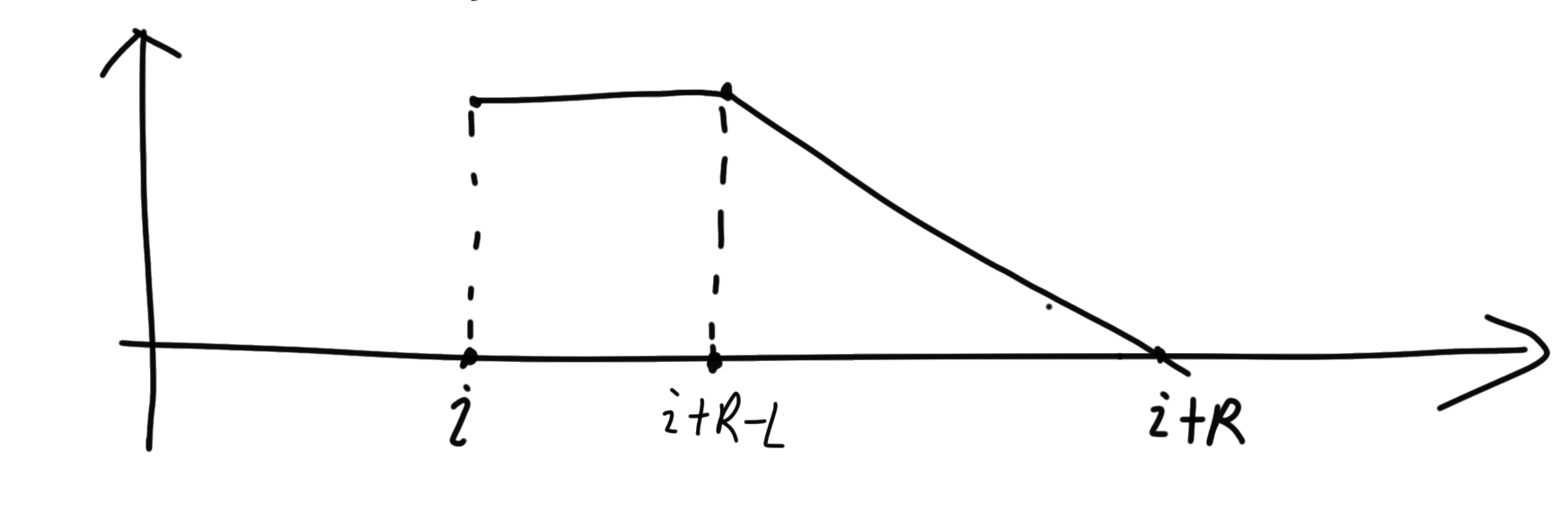
好的，题目的特征已经分析完了，接下来看看怎么做这道题吧。

三、算法分析

思路1：暴力枚举

最容易想到的思路是，对于每个位置 i，遍历所有区间，找到覆盖 i 的最大权值的极好区间，然后输出。
复杂度：O(n*q*R*(R-L+1))
得分：5 分。

for (int i = 1; i <= n; i++) {
  dpL[i] = INT64_MIN;
  for (int l = max(i - R + 1, 1); l <= i; l++) {                    // 枚举左边界
    for (int r = max(l + L - 1, i); r <= min(l + R - 1, n); r++) {  // 枚举右边界
      dpL[i] = max(dpL[i], preSums[r] - preSums[l - 1]);
    }
  }
}

思路2：线段树或RMQ

暴力枚举时，在逐个计算 preSums[r] - preSums[l - 1] 然后取最大值。
其中 l-1 是固定的，等价于求出区间内最大的 preSums[r]。

区间最大值，可以用线段树或RMQ来维护。
线段树复杂度：O(n*q*R*log(n))。
RMQ复杂度：O(n*q*R)。
这样就可以把性质B 区间长度不大于 32 的情况都解决了。
RMQ得分: 30 分。

思路3：L=R单调队列

性质 A 是 L=R，此时可以发现，r 固定时 l 也是固定的。

如果预处理出每个位置 r 的值，则又可以使用区间最大值的算法了。
由于不同的询问 L=R 不同，故每次询问都需要重新预处理 RMQ。
复杂度会很高。

区间大小固定，这不就是经典的滑动窗口吗？
滑动窗口内求最大值，可以用单调队列维护。
性质A的复杂度：O(n*q)
综合复杂度：O(n*q*R)。
得分：40分

思路3：错误的贪心

还是这个区间分布，很容易想到一个贪心思路：
先枚举所有 [i,i+L-1] 的右边界，求出最大值。
然后枚举 [i-L+1,i] 的左边界，求出最大值。
两个合起来，是不是就覆盖所有区间了。

每个左右边界为 i 的最大值可以使用单调队列预处理出来。

dpL[i] = max(sums[i,L], ..., sums[i,R])

然后对于 [i,i+L-1] 的区间边界，可以继续使用单调队列求出来。

dpLL[i] = max(dpL[i-L+1], ..., dpL[i]);

这样，左右两个方向合起来，就是位置 i 的答案。

dp[i] = max(dpLL[i], dpRR[i]);  

贪心复杂度：O(n*q)
性质 D 测试数据通过。
得分：45分。

为何贪心只能解决性质 D 呢？

如下图，当 L > n/2 时，左右贪心区间存在交集，所以可以覆盖所有区间。

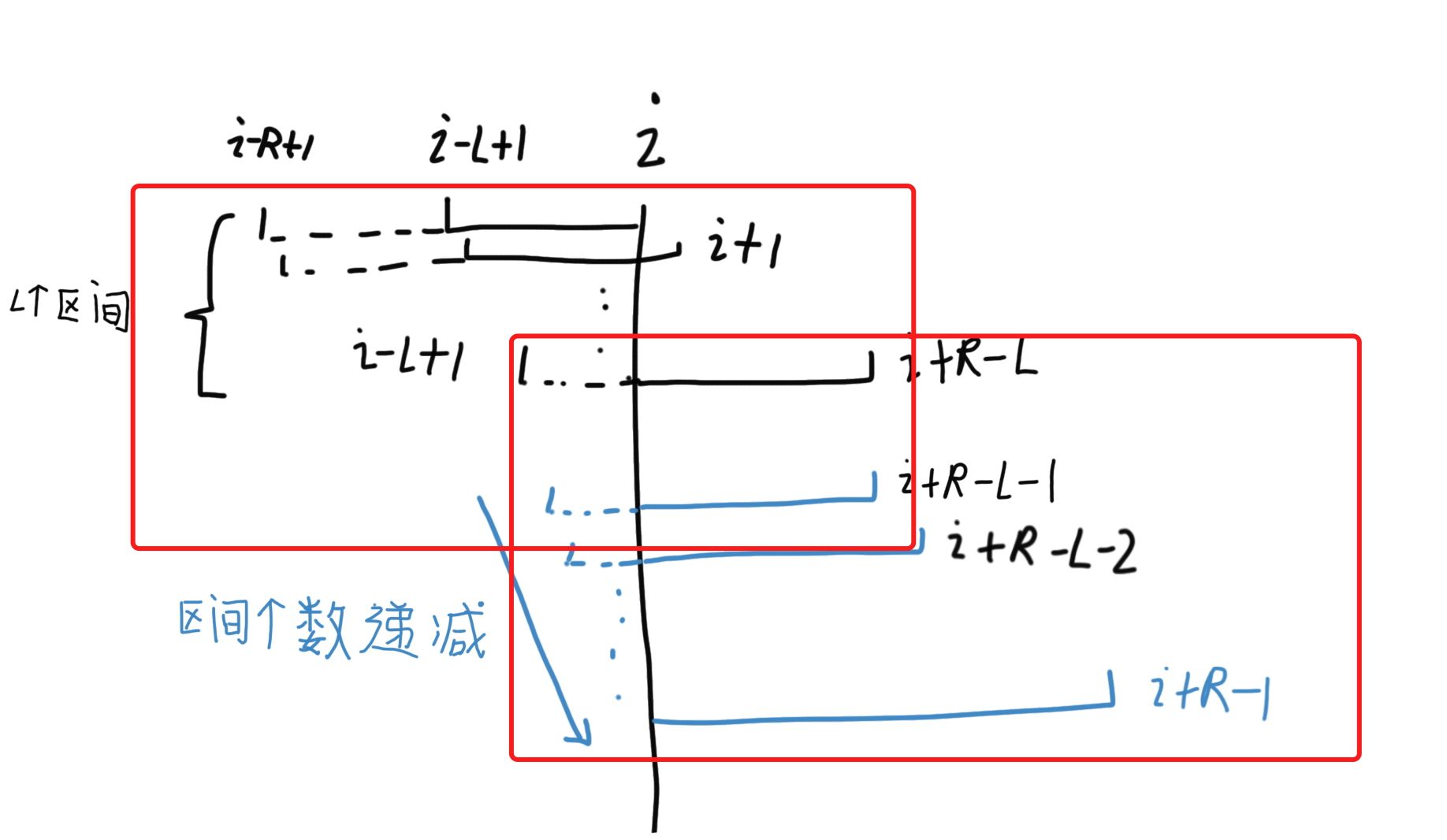
而 L 比较小的时候，部分区间无法被覆盖。
具体来说，就是 i+R-L > i+L-1 的时候，即 R > 2L-1 的时候无法被覆盖。
L > n/2 时, 2L > n， 不妨令 2L = n + 1。
则 R > 2L - 1 = n，即 R > n，显然不成立。

思路4：通用单调队列

只看一个位置 i，假设右边界是 i，合法左边界为 l ，则

dpR[i] = max(sum(l,i))
= max(sum(i) - sum(l-1))
= sum(i) + max(- sum(l-1))
= sum(i) - min(sum(l))

对于每个右边界 r，只有一个最优值，即合法区间的最小前缀和。

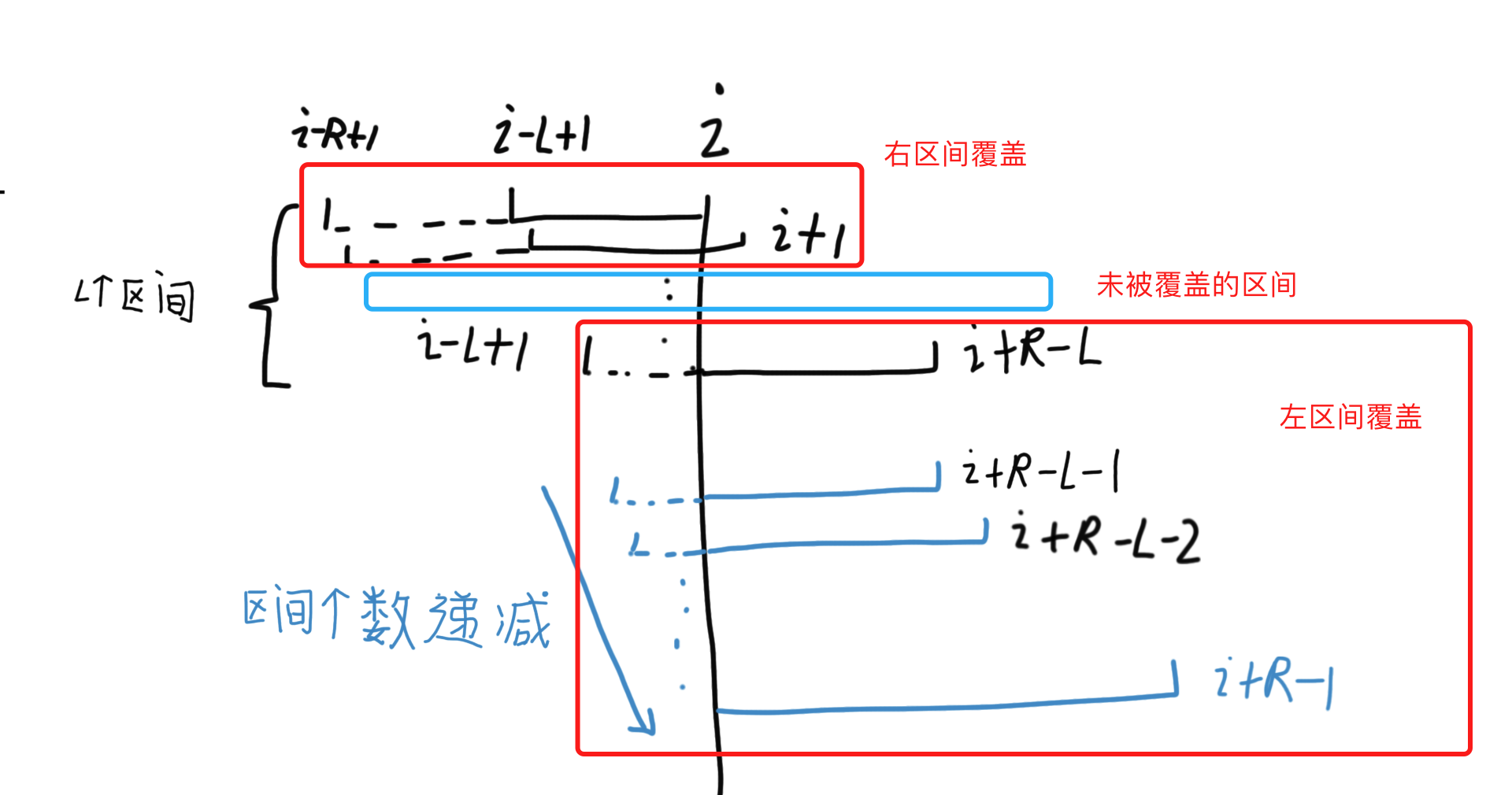
还是这个图，右边界 [i,i+R-L] 时，长度为 [L,R] 的区间都覆盖 i，最小前缀和不会改变。
显然，如果一个较大的右区间比一个较小的右区间更优时，较小的右区间是可以丢弃的。
所以，所有的合法右区间组成了一个单调队列。

但是，对于右边界 [i+R-L+1, i+R-1]，不存在长度为 L 的区间，且越靠右，合法区间个数越小。
当 i 向右移动时，右边界覆盖区间都会多一个，单调队列是否还成立呢？

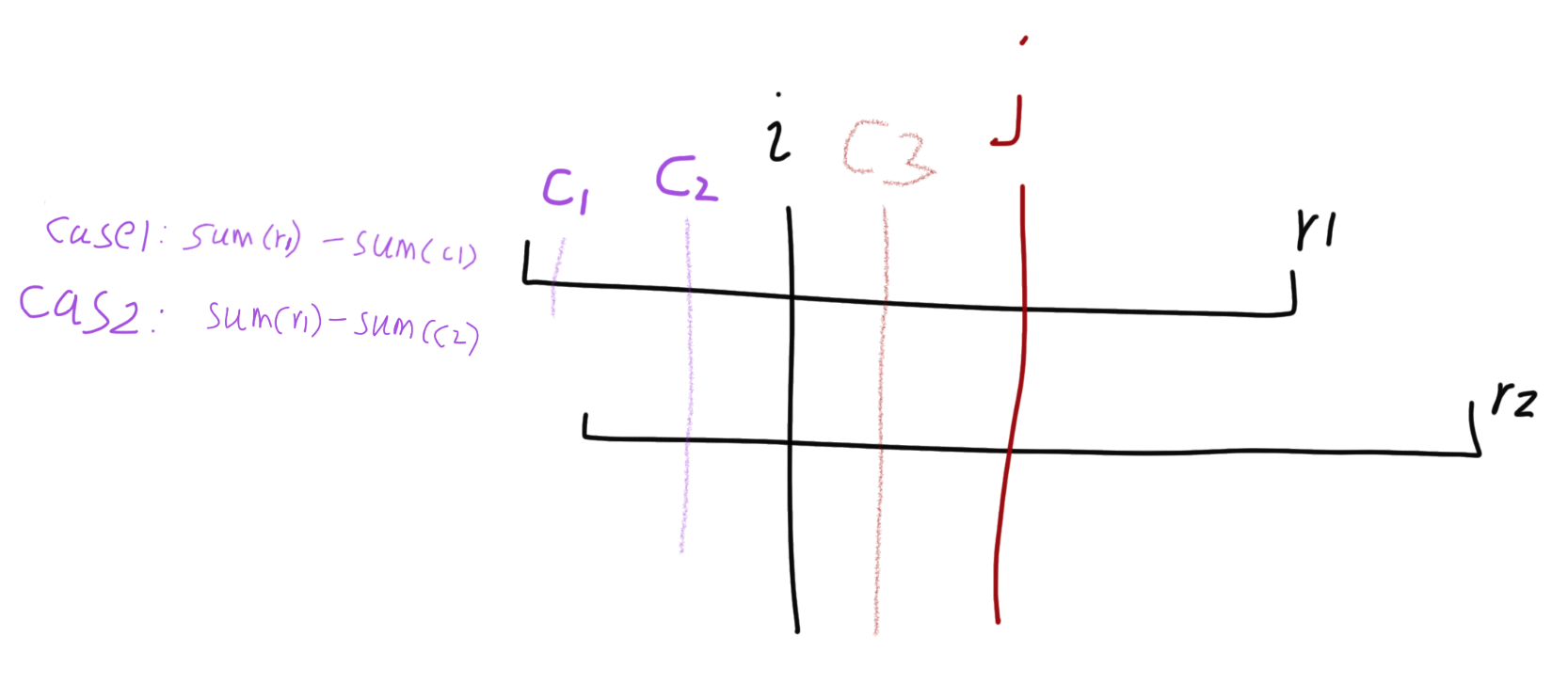
如图，右边界 r1 和右边界 r2 都覆盖了 i，但是没有覆盖长度为 L 的区间。
此时 r1 的最小值会分两种情况。

情况1：r1 的最小值 c1 比 r2 的最小值 c2 小。
此时 c1 肯定不在 r2 的合法区间内。

有这些公式，可以推导出 sum(r2) >= sum(r1)。

前提: sum(r2) - sum(c2)  >= sum(r1) - sum(c1)
case1: sum(c2) >= sum(c1)
推论1: sum(r1) - sum(c1) >= sum(r1) - sum(c2)
前提+推论： sum(r2) - sum(c2) >= sum(r1) - sum(c2)
结论: sum(r2)  >= sum(r1)

对于情况2也一样，因为 sum(r2) - sum(c2) >= sum(r1) - sum(c2)，所以 sum(r2) >= sum(r1)。

由此可以确定，当前面的右边界被贪心丢弃时，可以确定，前面的右边界的前缀和一定比后面的右边界小。
所以，i 向右移动遇到更小的前缀和 c3 时，单调性 sum(r2) - sum(c3) >= sum(r1) - sum(c3) 依旧成立。

由此，不需要关心右边界覆盖的区间后续会不会增多，覆盖 i 的所有右边界可以组成一个单调队列，从而计算出 i 位置的答案。

接下来思考：i 向右移动一位时，如何维护单调队列？

第一，右边界为 i-1 时，需要被删除，因为 i-1 这个右边界已经不能覆盖 i 了。
第二，右边界为 [i+L-1,i+R-2] 时，单调队列需要全部更新。因为这些右边界都加入了 [i,?]的区间，最小值可能会改变。
第三，加入未覆盖 i-1 的右边界 [i,i+R-L]。

第一步和第三步都好做，都是更新一个点。
但是第二步需要更新一批点，复杂度可能退化为 O(n)。
可以确定，需要更新的是那些最小值大于 sum(i-1) 的右边界。

观察这些最小值的关系，可以发现最小值也是单调递增的。

反证法：还是这个图。
假设 r2 的最小值 c2 比 r1 的最小值 c1 还小。
由于 r2 比 r1 靠右，两个长度相等，所以 i 的左侧 r1 是覆盖 r2 的。
故 r1 也覆盖了 c2，此时 r1 的最小值不可能是 c1。
所以假设不成立。

所以，可以对单调队列的一个后缀进行更新。
得分：95 分。

思路5：单调区间队列

分析思路4的暴力修改单调队列后缀的方法，发现大部分情况是最优的。
只有一种情况会导致性能恶化：最小值相等，右边界前缀和单调递减，这些后缀的最小值不断下降，从而扫描修改。

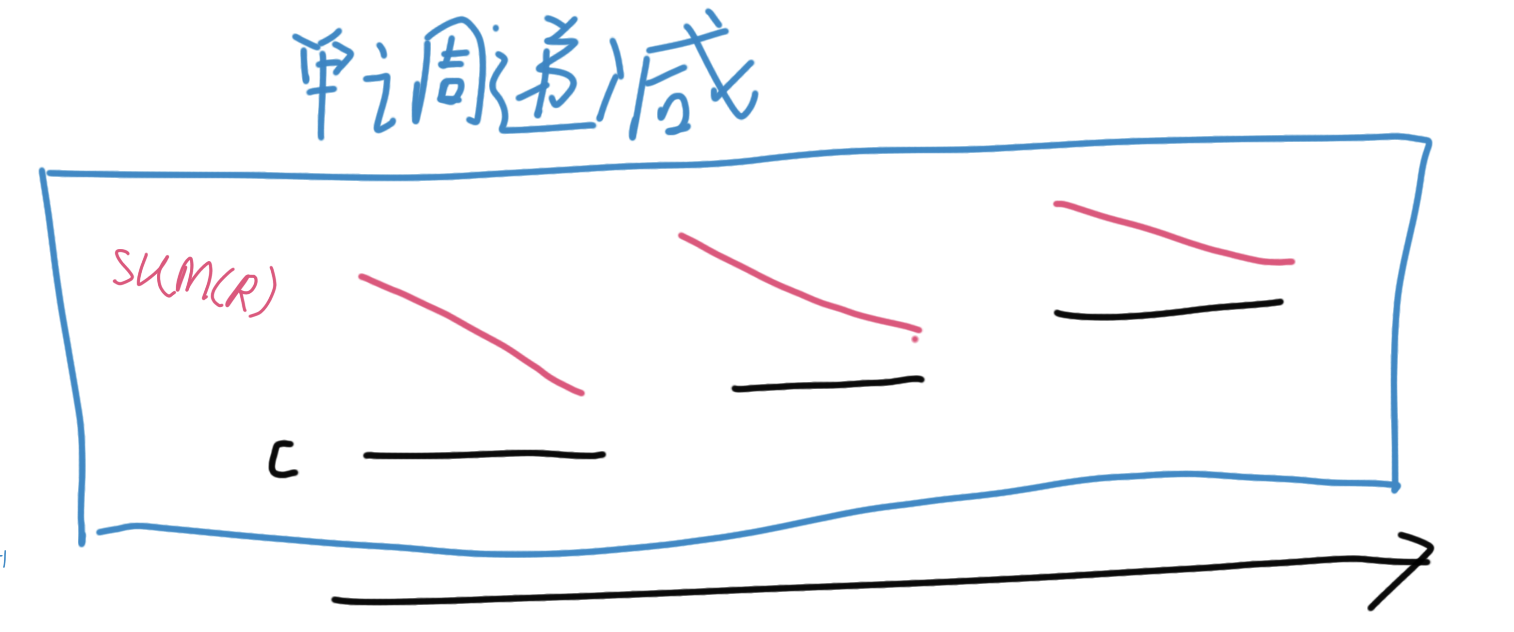
这时候很容易想到，最小值相等的区间进行合并，这样只需要修改最小值即可，右边界的单调性不会被破坏。

首先，需要将整体的单调队列拆分为两个队列：第一个是永远不会修改的，第二个是可能会被修改的。
对于会修改的队列，有两种实现方法：一种是双向链表，一种是数据结构来解决。

先思考一个问题：为何最小值相等的区间不能只保留最大右边界呢？
因为如果最大的右边界被删除后，剩余的区间还需要找到接下来的最大右边界。
这个关系目前是使用单调队列来维护的。

求区间的最大值，RMQ 不就可以 O(1)计算吗？
所以，对于相等的区间，不需要存单调队列了，直接存左右边界即可，最大值由 RMQ 来计算。

还有一个问题：由于整体队列要保持单调性，中间很多位置由于不是最优的被删除了，导致区间不是连续的。
这会导致有很多空隙，如何处理？

把有空洞的两个区间合并为一个区间，会影响答案吗？
不会，因为这些空洞就是因为值太小才被删除的，合并后，区间最大值也不会选择这些空洞。
故，右侧会修改的区间可以拆分为若干单调区间队列。

tuple<ll, int, int> queRight[max5]; // sum, l, r
int qRL, qRR;

复杂度分析：单调区间队列中每个元素顶多合并一次，故时间复杂度是 O(n)。
综合复杂度：O(nq)

四、代码实现

RMQ 代码是一个经典的模板，大家应该可以随手敲出来。

int base2[max5];
ll rmq[max5][20];

for (int i = 1; i <= n; i++) {
  rmq[i][0] = preSums[i];
}
for (int k = 1; k < 20; k++) {
  for (int i = 1; i <= n; i++) {
    rmq[i][k] = max(rmq[i][k - 1], rmq[min(i + (1 << (k - 1)), n)][k - 1]);
  }
}
base2[1] = 0;
for (int i = 2; i <= n; i++) {
  base2[i] = base2[i / 2] + 1;
}
ll MaxSum(int a, int b) { // RMQ O(1)查询区间最大值
  int k = base2[b - a + 1];
  return max(rmq[a][k], rmq[b - (1 << k) + 1][k]);
}

计算答案时，负数需要加上 2^64，这时候会越界。

最简单的方法是使用 int128。

__int128_t pow2_64 = (__int128_t(1) << 64);
ull Fix(ll k) {
  ull kk = 0;
  if (k < 0) {
    __int128_t t = k;
    t += pow2_64;
    kk = t;
  } else {
    kk = k;
  }
  return kk;
}

一种取巧的方式是分治，即可以把负数加法改成正数减法，先使用 2^63减，之后再加上2^63，就不会越界了。

ull pow2_63 = (ull(1) << 63);
inline ull Fix(ll k) {
  ull kk = 0;
  if (k < 0) {
    k = -k;
    kk = pow2_63 - k + pow2_63;
  } else {
    kk = k;
  }
  return kk;
}

当然，如果你了解二进制储存的话，会发现负数转无符号，恰好是加上 2^64。

例如以 1 字节为例， -5 的二进制是 11111011。
5 的二进制是 00000101。
两个相加恰好是 2^8。

inline ull Fix(ll k) {
  return ull(k);
}

单调队列也是滑动窗口的经典模板。

/*
性质A: L == R
覆盖 i 的区间： [i-L+1, i], ..., [i, i+R-1]
定义 S(a) = sum(a, a+L-1)
则 ans[i] = max(S(a),S(a+1),...,S(a+L-1))
思路1：线段树/RMQ
思路2：单调队列
*/
ull SolverA(int L, int R) {
  ull ans = 0;
  qL = 0, qR = 0;
  for (int l = 1; l <= n; l++) {  // [l-L+1, l], ..., [l, l+R-1]
    int r = l + L - 1;
    if (r <= n) {  // 入队
      ll sum = preSums[r] - preSums[l - 1];
      while (qL < qR && que[qR - 1].first <= sum) {
        qR--;
      }
      que[qR++] = {sum, l};
    }
    ll k = que[qL].first;  // 肯定有答案
    ans ^= Fix(k * l);
    // 删除 pos = l + L - 1
    if (qL < qR && que[qL].second == l - L + 1) {
      qL++;
    }
  }
  return ans;
}

所有代码已经上传到网盘了。

五、总结

总的来看这道题，还挺难的。

如果只想到 RMQ，只能得 30 分。
再加上性质A和性质D，可以得 45 分。

再之后，需要能够意识到，所有右边界都进行单调队列处理，然后再考虑修改单调队列的后缀，就可以得到 95 分了。
最后 5 分则需要对单调队列进行合并，从而才能得满分。

另外这道题卡常数卡得很厉害，需要删除各种误用的空间，或者复用空间才行。

《完》

-EOF-

本文公众号：天空的代码世界
个人微信号：tiankonguse
公众号 ID：tiankonguse-code