NOIP 2025 第四题 序列询问 query 几何题解

作者: tiankonguse | 更新日期:

单调队列用到极致。

本文首发于公众号：天空的代码世界，微信号：tiankonguse

零、背景

之前已经在《PDF 题目分享》中分享了 NOIP 2025 的题目，在《糖果店 candy 题解》里给出了第一题的题解，在《清仓甩卖 sale 题解》给出了第二题的题解，在《序列询问 query 单调队列 题解》中给出了第四题的单调队列视角题解。

这篇文章则从几何的角度，再来分享 NOIP 2025 第四道题「序列询问 query」的另一种理解方式，也可以和上一篇单调队列的做法形成对照。

PS：题目 PDF、官网测试数据、题解代码已上传网盘，公众号回复 NOIP-2025 获取。
PS2：最近工作上比较忙，所以更新会比较慢，见谅。

源码截图

一、题目

给定一个长度为 n 的整数序列 a1, a2, . . . , an。
有 q 次询问，其中第 j 次询问会给出一个区间长度范围 [L, R]。
定义区间 [l, r] 是极好的，当且仅当区间 [l, r] 的长度在 [L, R] 之间（含端点）。
定义区间 [l, r] 的权值为 S(l,r) = sum(a[l],...,a[r])。
对于所有 i = 1, 2, . . . , n，求出所有包含 i 的极好区间中的最大权值，即 max{ S(l,r) | l <= i <= r }。

对于每次询问，设包含 i 的极好区间的最大权值为 ki，输出一行一个非负整数，表示 XOR((ki * i) % 2^64)。
其中 XOR 表示二进制按位异或。
注意：对于任意整数 x，存在唯一的非负整数 y 满足 y ≡ x (mod 2^64)。

源码截图

二、题意分析

首先是理解题意。
对于每个位置 i，需要找到覆盖 i 的最大权值的极好区间。

那覆盖 i 的极好区间有哪些呢？

源码截图

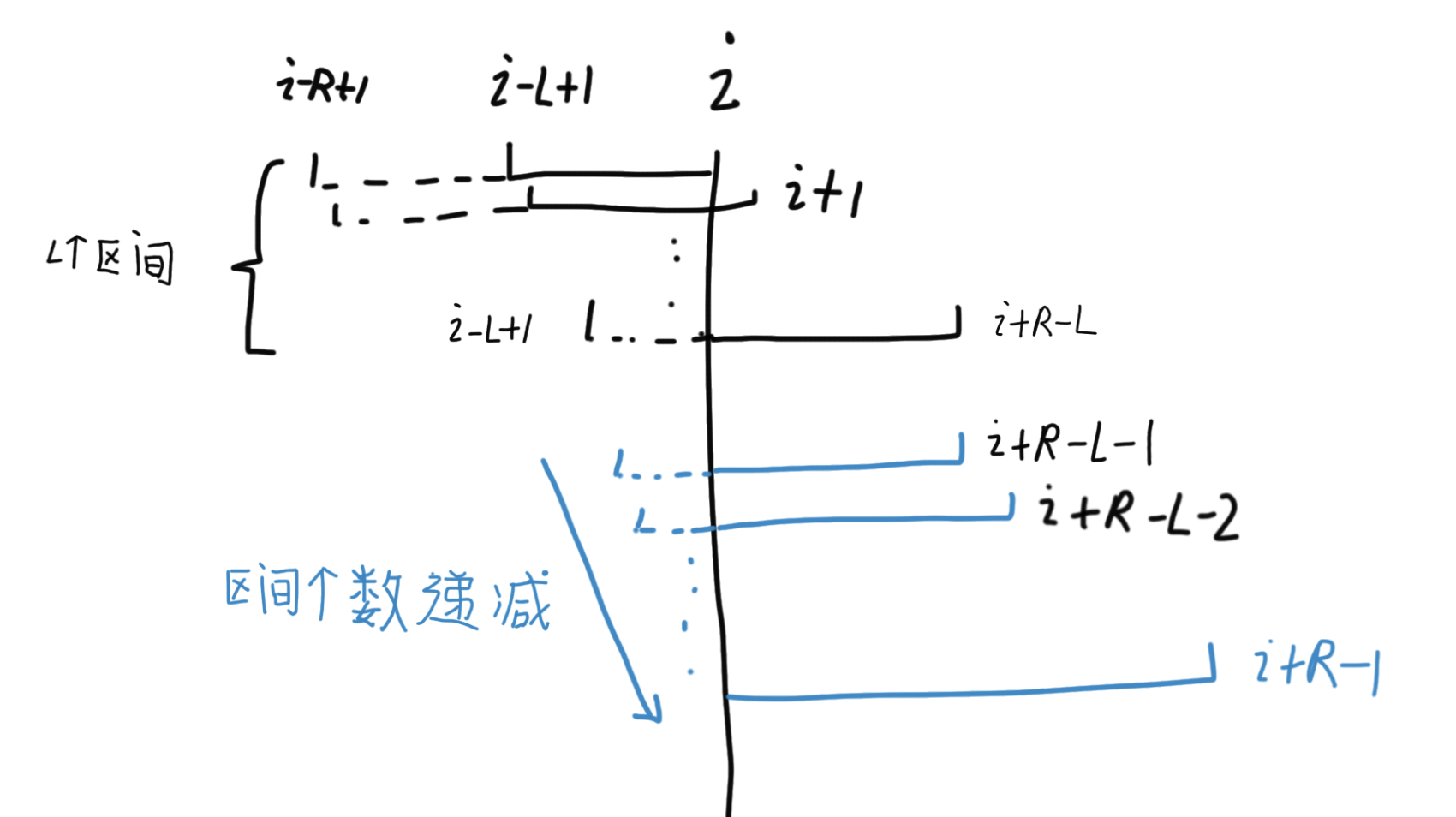
如上图，可以根据区间的右边界来进行划分分组。
以 [i, i+R-L] 为右边界时，长度为 [L, R] 的极好区间都是存在的，即都有 R-L+1 个极好区间。
i+R-L 是一个分界线，再往右，长度最短为 L 的极好区间就不存在了，即极好区间个数减一个。
再往右，每右移一位，极好区间的最短长度就加一，极好区间个数就减一。

这个覆盖 i 的极好区间的分布特征如下，分为两段，第一段是满的，第二段递减。

源码截图

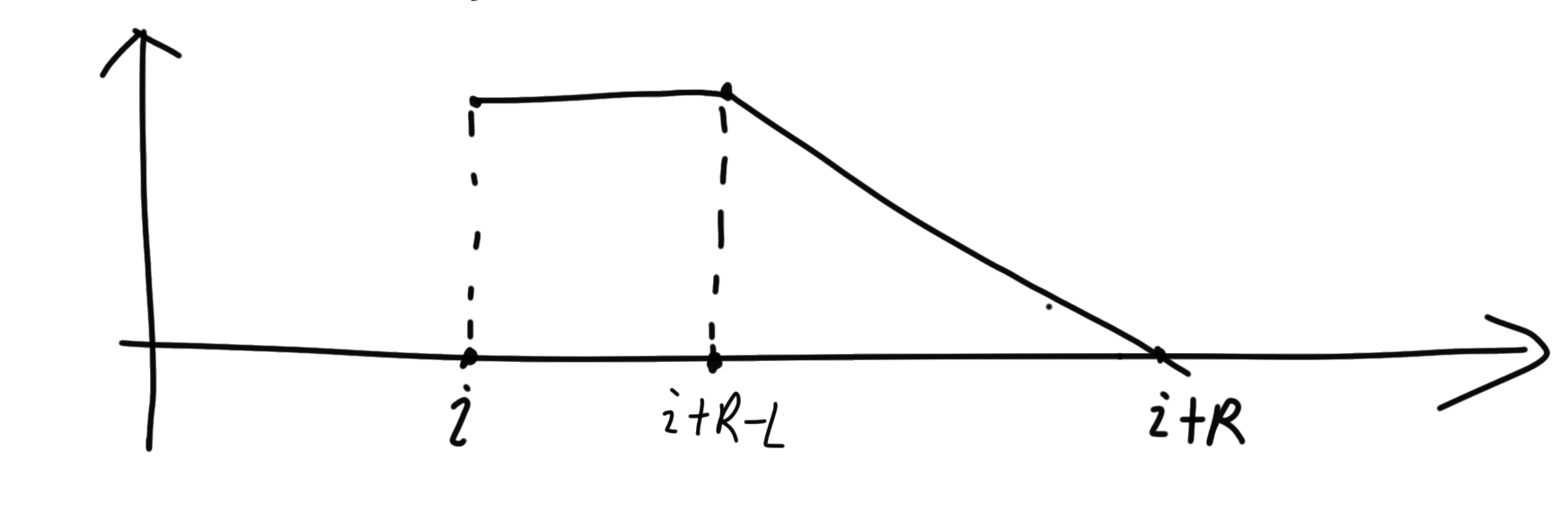
从这个角度看，所有覆盖 i 的极好区间在 (l, r) 平面上会形成一个规则的梯形，这是后面几何做法的基础。

三、算法分析

在《单调队列 题解》中，已经介绍了各个特殊性质的部分分做法。

暴力枚举，5 分。
RMQ 区间最值减少一层循环，解决性质 B，30 分。
性质 A L=R 单调队列特殊处理，40 分。
错误的贪心解决性质 D，45 分。
暴力修改的单调队列，95 分。
区间合并的单调队列，100 分。

上面的思路大多还是一维的：围绕前缀和、区间最值和单调队列做各种优化。
接下来把所有区间放到二维坐标系里，用几何图形来刻画「极好区间」的整体形状，从而推导出另一个视角的解法。

如果把区间 [l, r] 当做二维坐标系中的一个点，l 是横坐标，r 是纵坐标，则所有满足条件的区间如图所示，会形成一个梯形。

源码截图

如下图，可以发现，通过两个平行四边形就可以覆盖整个梯形。
其中蓝色背景的平行四边形，就是左边界为 [i-L+1, i] 的极好区间。
红色背景的平行四边形，就是右边界为 [i, i+L-1] 组成的极好区间。
这个也是上篇文章中错误贪心的几何意义。

源码截图

通过调整 L 与 R 的比例，可以发现，当 2*L < R 时，两个平行四边形无法完全覆盖梯形。

源码截图

所以，我们需要对这个梯形进行进一步划分，使得若干个图形可以完全覆盖整个梯形。

首先是把梯形划分为一个平行四边形和一个等腰直角三角形。

源码截图

对于这块等腰直角三角形，可以根据中点，划分为两个平行四边形和一个正方形。
如下图，粉红色边框的平行四边形、浅蓝色边框的平行四边形、紫色边框的正方形。

源码截图

对于平行四边形，计算方法与之前相同，都是两轮单调队列来计算。

而对于中间的正方形，可以做如下推导。

f(x) = max(sum(x, y), ..., sum(x, y+a))  
= max(sum(y) - sum(x-1), ..., sum(y+a) - sum(x-1));
= max(sum(y),...,sum(y+a)) - sum(x-1)


max(f(x0), ..., f(x1))
 = max(
   max(sum(y),...,sum(y+a)) - sum(x0-1)
   ...
   max(sum(y),...,sum(y+a)) - sum(x1-1)
 )
= max(sum(y),...,sum(y+a)) + max(
   - sum(x0-1)
   ...
   - sum(x1-1)
 )
= max(sum(y),...,sum(y+a)) - min(sum(x0-1),...,sum(x1-1))

推导的结论就是：只需要求一个区间的最大值减去另一个区间的最小值即可。
区间最大值和最小值依旧可以使用单调队列或者 RMQ 来做。

源码截图

不过我使用 RMQ 来求最值，只得到 60 分。
再结合特殊性质，最高得到 75 分。
最后有 5 组数据一直是超时。

大致算一下常数：预处理最大值和最小值的 RMQ，复杂度是 n log(n)。
计算 3 个平行四边形和 1 个正方形，要循环 4 遍，加上初始化一遍和求答案一遍，共循环 6 遍，复杂度就是 O(6*n*q)。

之后又优化了一下初始化逻辑，把几个循环合并到一个循环，最后一组样例也通过了，得分提升到 80 分。

源码截图

由于时间关系，就没有继续做常数优化了。
我本地运行不到 1 秒，但在 OJ 上还是会被卡常，始终没能拿到满分。

源码截图

四、代码实现

根据上述的讨论，可以把梯形划分为三个平行四边形和一个正方形。

ull Solver(int L, int R) {
  int a = (R - L) >> 1;  // 正方形边长
  for (int i = 1; i <= n; i++) {
    dp[i] = INT64_MIN;
  }
  SolverL(L - 1, R - 1, 0, L - 1);              // 梯形的左半部平行四边形
  SolverL(L - 1 + a, R - 1, L - 1, L - 1 + a);  // 三角形右上的平行四边形
  SolverR(L - 1 + a, R - 1, 0, a);              // 三角形左下的平行四边形
  SolverSquare(L - 1, a);                       // 三角形内的正方形

  ull ans = 0;
  for (int i = 1; i <= n; i++) {
    ans ^= Fix(dp[i] * i);
  }

  return ans;
}

由于需要计算两个不同偏移量的平行四边形，所以需要进行封装，方便复用一个函数。

源码截图

还是这张图，观察浅黄色平行四边形和浅蓝色平行四边形，可以发现：

1）两个平行四边形的左右两条边是垂直于 Y 坐标轴的。
2）两个平行四边形的左下角是水平对齐的，只是偏移量不同。
3）水平方向上，左右边分别有一个偏移量。
4）垂直方向上，上下边也分别有一个偏移量。

故，可以根据左右的偏移量以及上下界的偏移量，来进行封装，实现一个通用的计算平行四边形的函数。

void SolverL(int D, int U, int minDis, int maxDis) {
  // 第一步：计算以 i 为左端点，长度为 [D,U] 的所有极好区间的最大权值
  for (int i = 1; i <= n; i++) {
    int l = i + D;
    int r = i + U;
    if (l > n) {
      dpTmp[i] = INT64_MIN;
    } else {
      r = min(r, n);
      dpTmp[i] = MaxSum(l, r) - preSums[i - 1];
    }
  }
  // 第二步：计算以 [i-maxDis+1,i-minDis+1] 为左端点，长度为 [D,U] 的所有极好区间的最大权值
  qL = 0, qR = 0;
  int l = 0, r = 0;
  for (int i = 1 + minDis; i <= n; i++) {
    if (i - minDis < 1) continue;  // 无效区间
    // pop dpL[pos] if pos < i - maxDis
    while (qL < qR && que[qL].second < i - maxDis) {
      qL++;
    }
    // add dpL[i-minDis]
    while (qL < qR && que[qR - 1].first <= dpTmp[i - minDis]) {
      qR--;
    }
    que[qR++] = {dpTmp[i - minDis], i - minDis};
    UpdateAns(i, que[qL].first);
  }
}

对于 SolverR，与 SolverL 类似，不再赘述。

对于正方形，也是定义一个偏移量和边长即可。

void SolverSquare(int L, int a) {
  if (a == 0) return; // 剪枝，不存在边长为 a 的正方形
  for (int i = 1; i <= n; i++) {
    if (i - L < 1) continue;
    ll tmp = MaxSum(i, min(n, i + a)) - MinSum(max(0, i - L - a - 1), i - L - 1);
    UpdateAns(i, tmp);
  }
}

五、总结

很多看起来是一维区间的题目，映射到坐标轴之后，其实就是一个二维几何问题。
然后通过几何图形的拆分，就可以用一些简单的几何图形拼出目标几何图形，对应到算法上就是把复杂区间拆成若干类结构相对简单的区间去做。

面对平行四边形，我曾经还想直接写一个二维 RMQ 来计算。
但是发现空间复杂度会比较高，是 O(n log(n) log(n))，所以最终还是放弃了这种做法。

《完》

-EOF-

本文公众号：天空的代码世界
个人微信号：tiankonguse
公众号 ID：tiankonguse-code

本文首发于公众号：天空的代码世界，微信号：tiankonguse
如果你想留言，可以在微信里面关注公众号进行留言。

关注公众号,接收最新消息

置顶文章

tiankonguse + ≡
穿越