OI 必学：DFS序

零、背景

在 OI 比赛中，我们经常会遇到各种关于树的修改和查询问题。

而我们日常使用的数据结构，如线段树、树状数组，通常都是维护连续区间。

如果我们能把树上的节点映射到一段连续区间上，这类问题往往就能转化为熟悉的区间问题，从而迎刃而解。

本文主要介绍一种常用的树转换方法：DFS 序，并通过几个典型应用，帮助大家建立起对这类问题的整体认识。

一、DFS 序的定义

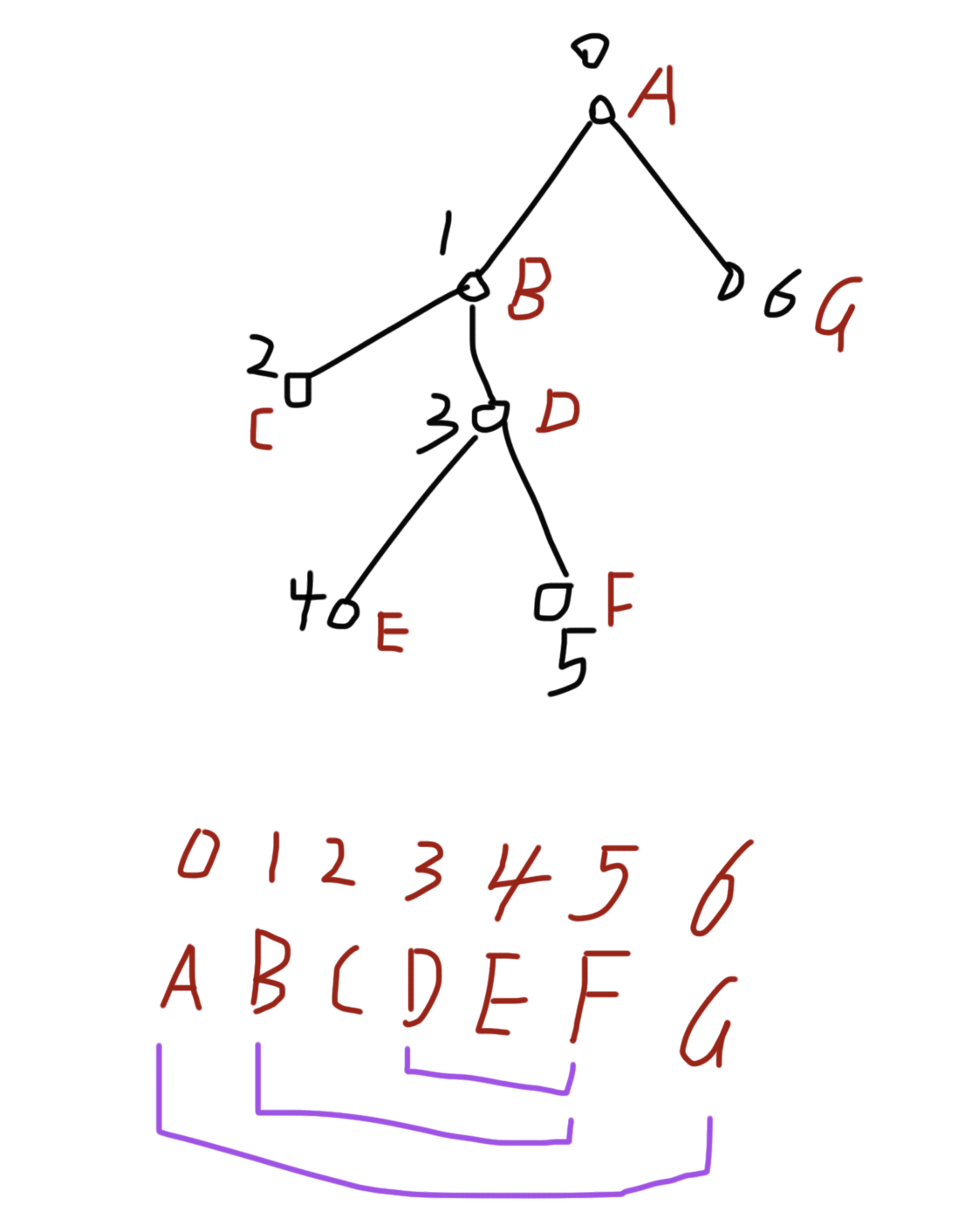
DFS 序，就是在对一棵树进行深度优先搜索（DFS）时，按照访问顺序记录下来的节点序列。

我们把每次「第一次访问到某个节点」的时刻记录下来，就得到一个长度为 n 的序列，这个序列就叫做 DFS 序。

在实现时，通常会同时维护三类信息：每个节点的进入时间、离开时间，以及某个时间戳对应的是哪个节点。

vector<int> dfn;  // dfs 序
vector<int> in;   // 进入时间
vector<int> out;  // 离开时间
int t = 0;

void BuildDfn(const int u, const int p) {
  in[u] = t;
  dfn[t] = u;
  t++;
  for (int v : g[u]) {
    if (v == p) continue;
    BuildDfn(v, u);
  }
  out[u] = t;
}

观察 DFS 序，可以发现它有一个非常关键的性质：

1）dfn 是一个长度为 n 的序列，其中 n 是节点数。
2）对任意一个节点 u，它的整棵子树在 DFS 序中对应的是一段连续区间 [in[u], out[u]]。

正是因为这个「子树对应连续区间」的性质，我们才能把树上的很多操作转化为区间上的操作，从而使用线段树、树状数组等经典数据结构来解决。

二、DFS 序的应用

下面通过几个常见的模型，看看 DFS 序是如何发挥作用的。

应用1：单点修改，子树查询

问题：给定一棵树，每次修改一个节点，查询某个节点子树中所有节点的权值和。

做法：先用 DFS 序把树「摊平」到区间上，每个节点对应区间中的一个位置。然后用线段树或树状数组，在这个数组上做单点更新与区间求和。

此时，节点 u 的整棵子树对应区间就是 [in[u], out[u]]，在这个区间上做一次区间查询即可得到子树权值和。

应用2：子树修改，子树查询

问题：给定一棵树，每次对某个节点的整棵子树做加减操作，查询某个节点子树中所有节点的权值和。

做法：同样先建立 DFS 序，把树转成连续区间，然后在 [in[u], out[u]] 这个区间上做区间加、区间求和。可以使用支持区间修改与区间查询的数据结构，例如带懒标记的线段树或差分 + 前缀和。

应用3：树链修改，单点查询

问题：给定一棵树，每次对一条树链 (u, v) 上所有节点的权值同时加上某个值 a，然后支持单点查询某个节点当前的权值。

思路：仍然先用 DFS 序把树转成区间，但这次不直接在树链上做操作，而是把「树链加」转化为若干次以根为起点的路径加。

具体可以这样做：

先对 u 增加 a，即 Add(u, a)，含义是把从根到 u 这条路径上的节点权值都加上 a。
然后对 v 增加 a，即 Add(v, a)，含义是把从根到 v 这条路径上的节点权值都加上 a。

此时，从根到 lca(u, v) 的这条公共前缀路径被加了两次，从根到 fa(lca(u, v)) 的路径也被间接多加一次，需要再把多加的部分抵消掉：

于是，再对 lca(u, v) 减去 a，即 Add(lca(u, v), -a)，含义是让 (root, lca(u, v)) 这条路径整体减去 a。
最后，对 fa(lca(u, v)) 再减去 a，即 Add(fa(lca(u, v)), -a)，含义是让 (root, fa(lca(u, v))) 这条路径整体减去 a。

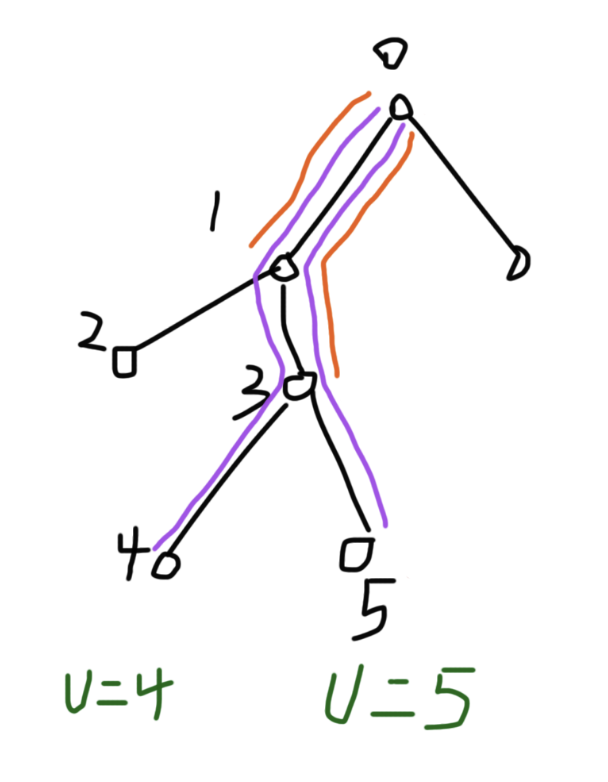
单点查询某个节点 u 的权值时，本质上就是把子树上所有会对它产生贡献的标记累加起来，这些标记通过子树区间和即可得到。

应用4：单点修改，树链查询

问题：给定一棵树，每次只修改一个节点的权值，查询树链 (u, v) 上所有节点权值之和。

这个模型和「树链修改，单点查询」刚好是相反的方向。

一种常见的做法是：让每个节点维护「从根到当前节点路径上的权值和」，也就是把树上的信息按根到节点的路径前缀和来存。

单点更新时，更新的节点会影响它所在子树中所有节点的根路径和，因此可以在 DFS 序对应的子树区间内做一次区间更新。
树链查询 (u, v) 时，可以先分别求出 (root, u) 和 (root, v) 两条路径的权值和，再减去 (root, lca(u, v)) 的权值和，最后再减去 (root, fa(lca(u, v))) 的权值和，就得到了树链 (u, v) 上的答案。

三、最后

只记录每个节点被第一次访问到的时间（进入时间），并据此得到的序列，一般就被称为 DFS 序。

如果同时记录进入时间和离开时间，就可以得到更完整的欧拉序。

在很多竞赛题里，欧拉序相关的技巧往往都可以通过 DFS 序配合合适的数据结构来实现，因此作为入门，先把 DFS 序这一工具掌握牢固就足够应付绝大部分常见问题了。

对于更复杂的「子树 + 树链」混合修改与查询问题，还可以在 DFS 序的基础上叠加重链剖分、差分、树上前缀和等更高级的技巧，这部分内容会在后续文章中单独展开。

《完》

-EOF-

本文公众号：天空的代码世界
个人微信号：tiankonguse
公众号 ID：tiankonguse-code