OI 必学：虚树

零、背景

在 OI 比赛中，我们经常会遇到各种关于树的问题。
这些问题往往与路径、子树、距离等性质相关。

前文已经介绍了《DFS 序》和《LCA》。
本篇将继续在这两者的基础上，介绍「虚树」这一常用技巧及其应用。

一、一个问题

题意：给一棵无根树，每个节点属于一个分组。
要求对于每个分组，统计分组内所有点对之间路径长度（边数）之和，并将所有分组的结果累加。

先从一个简单情况入手。
性质 A：所有点都在同一个分组内。
这时可以认为「没有分组」的概念，问题就退化为：求整棵树上所有点对之间路径长度（边数）之和。

算法思路：边的贡献法。
枚举每一条边，计算这条边对答案的贡献。
对于一条边，如果一侧有 个点，另一侧有 m 个点，那么这条边对答案的贡献就是 n*m。
整体复杂度为 O(n)。

具体实现：假设树的节点总数为 n，某个节点为子树根时，其子树大小为 m，则该节点到父节点的边对答案的贡献为 m * (n-m)。
因此，我们只需枚举所有子树根节点，累加它们到父亲这条边的贡献即可。

ll ans = 0;
int Dfs(const int u, const int p) {
  ll uNum = 1;
  for (auto v : g[u]) {
    if (v == p) continue;
    int vNum = Dfs(v, u);
    ans += vNum * (n - vNum);
    uNum += vNum;
  }
  return uNum;
}

再来看一个稍微复杂的情况。
性质 B：分组的数量只有 g=10 个。
思路：由于分组个数较小，可以枚举每个分组，分别计算该分组内部所有点对的答案，然后将结果相加。
具体实现：先统计当前分组内节点总数 groupAllNum，在 DFS 时对于每棵子树，只统计分组 ID 等于当前枚举分组 ID 的节点数。
整体复杂度为 O(g * n)。

ll ans = 0;
int Dfs(const int u, const int p, const ll groupId, const ll groupAllNum) {
  ll uNum = 0;
  if (group[u] == groupId) {
    uNum = 1;
  }
  for (auto v : g[u]) {
    if (v == p) continue;
    int vNum = Dfs(v, u, groupId, groupAllNum);
    ans += vNum * (groupAllNum - vNum);
    uNum += vNum;
  }
  return uNum;
}

如果分组个数继续增大，甚至接近节点数量级时，按分组枚举整棵树的做法就不再高效，这时就需要用到「虚树」了。

二、虚树的定义

先看下面这张图。假设红色的节点 2 和节点 4 同属一个分组。
在只考虑这个分组时，节点 1、3、5、6、7 以及与它们相关的边，都不会对答案产生贡献。
因此，我们可以删去这些无关节点与边，只保留分组内的节点 2、4，并在它们之间构造一棵新的树，在这棵树上直接计算答案。
这样，对所有分组分别构造出的这些小树的总节点数是 O(n) 级别的。

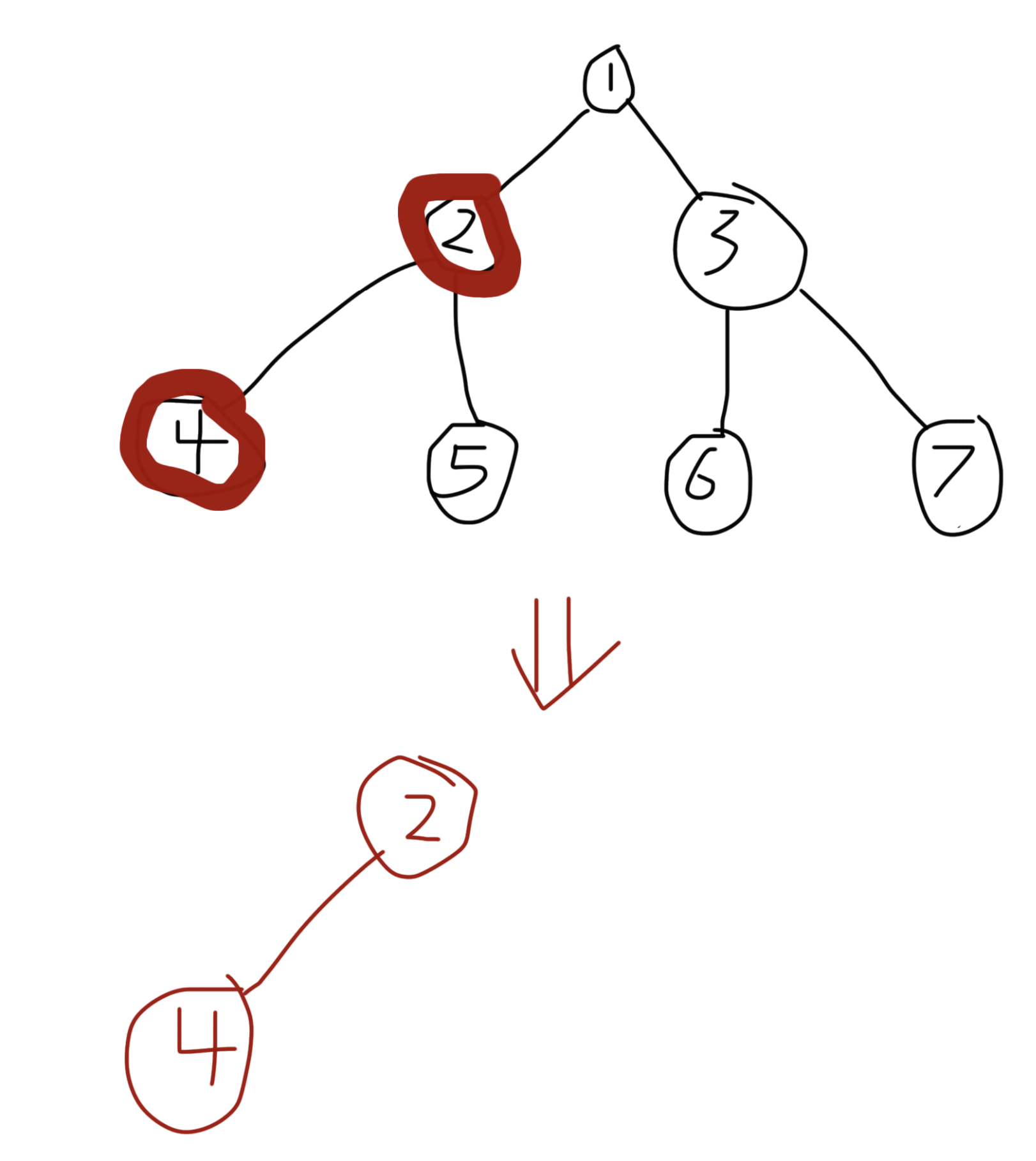
接着再看第二张图。
如果一个分组中，某些节点之间的路径上包含多条连续的边，我们可以把这几条边「压缩」成一条带权边。
此时，在压缩得到的新树上，每条边都需要带上一个权值，表示它实际对应的原树中的边数。

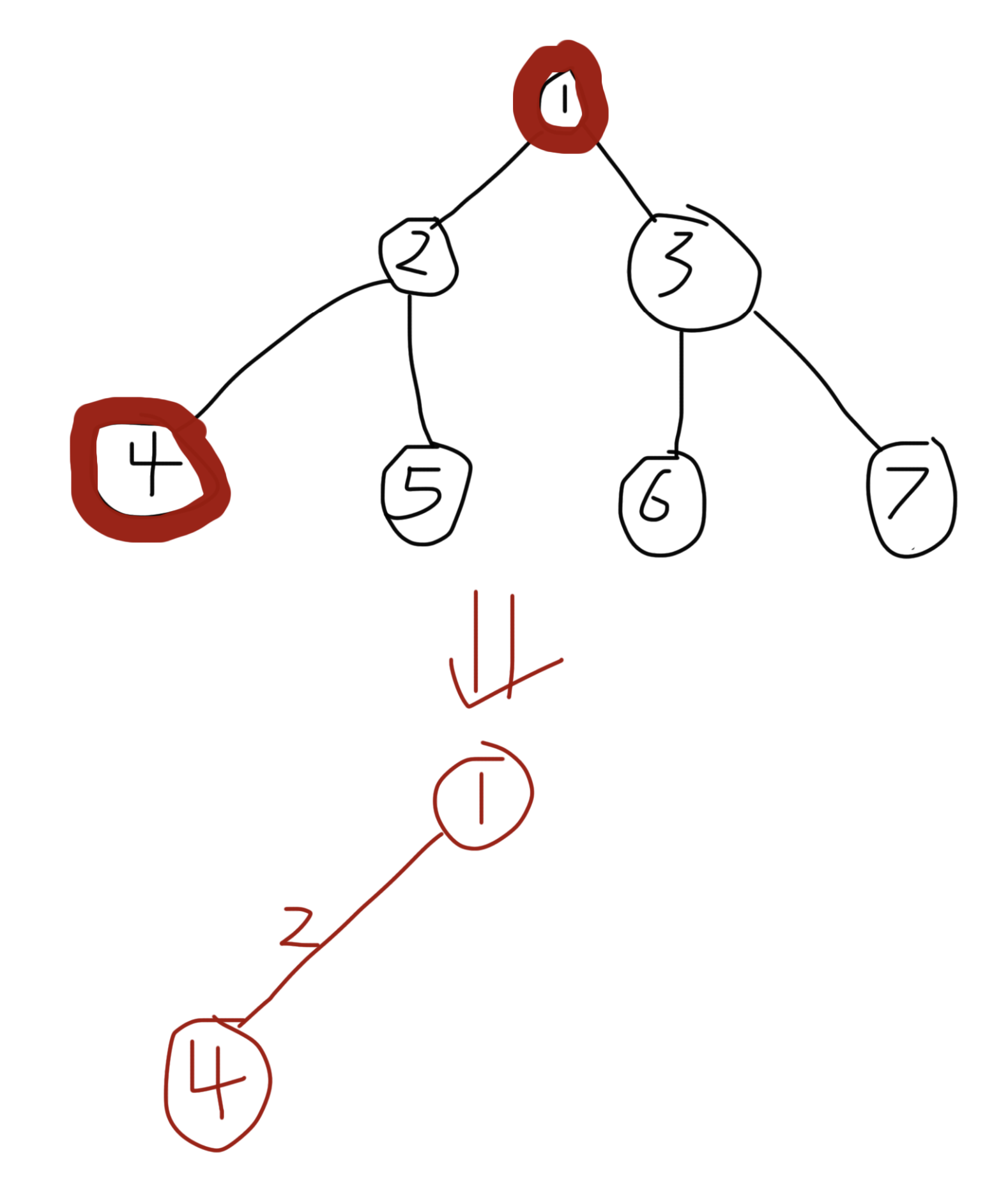
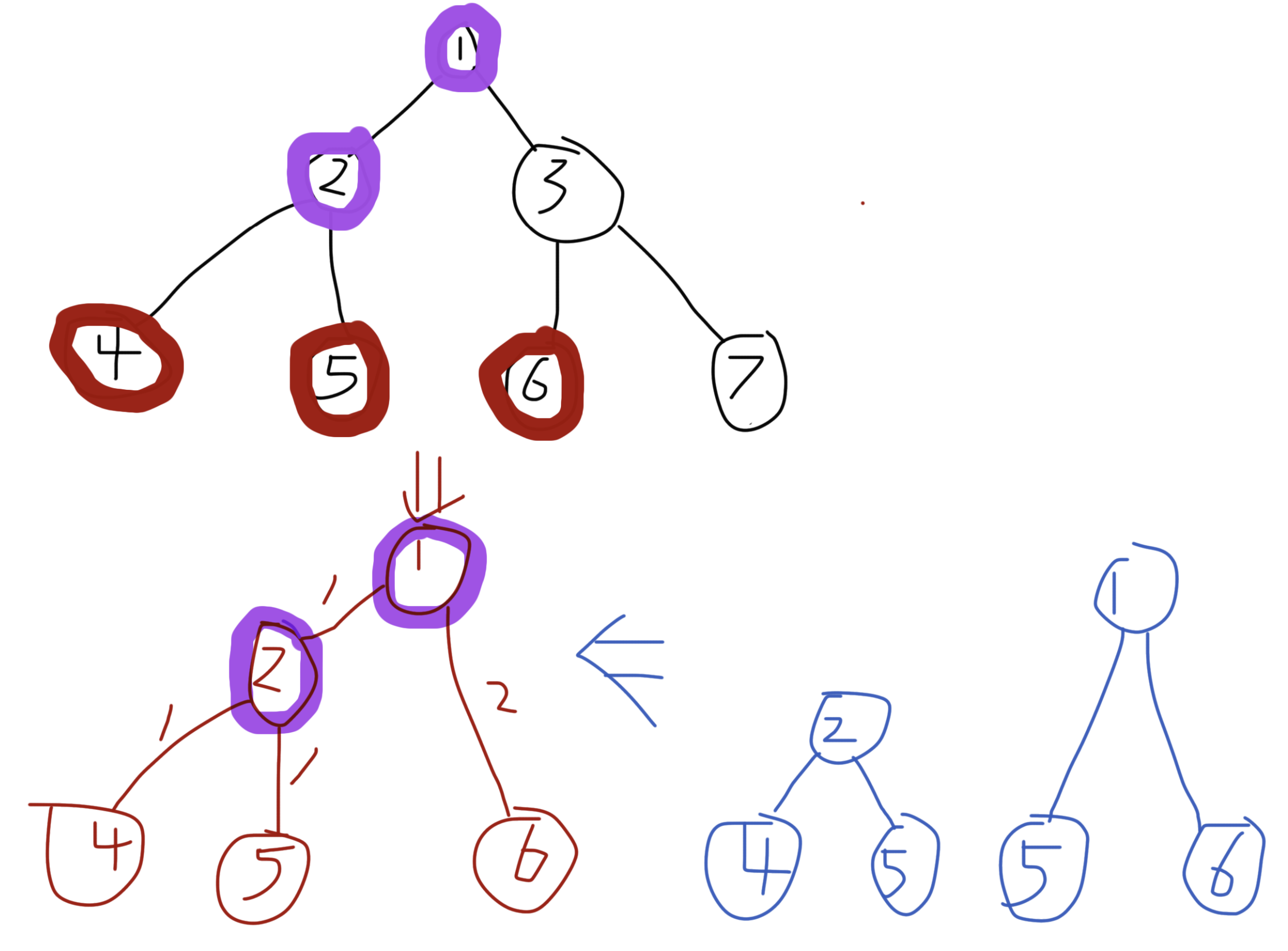
再来看第三张图。
当分组内多条路径之间存在交点时，这些交点（也就是相应路径的 LCA）也必须作为新树中的节点保留下来。

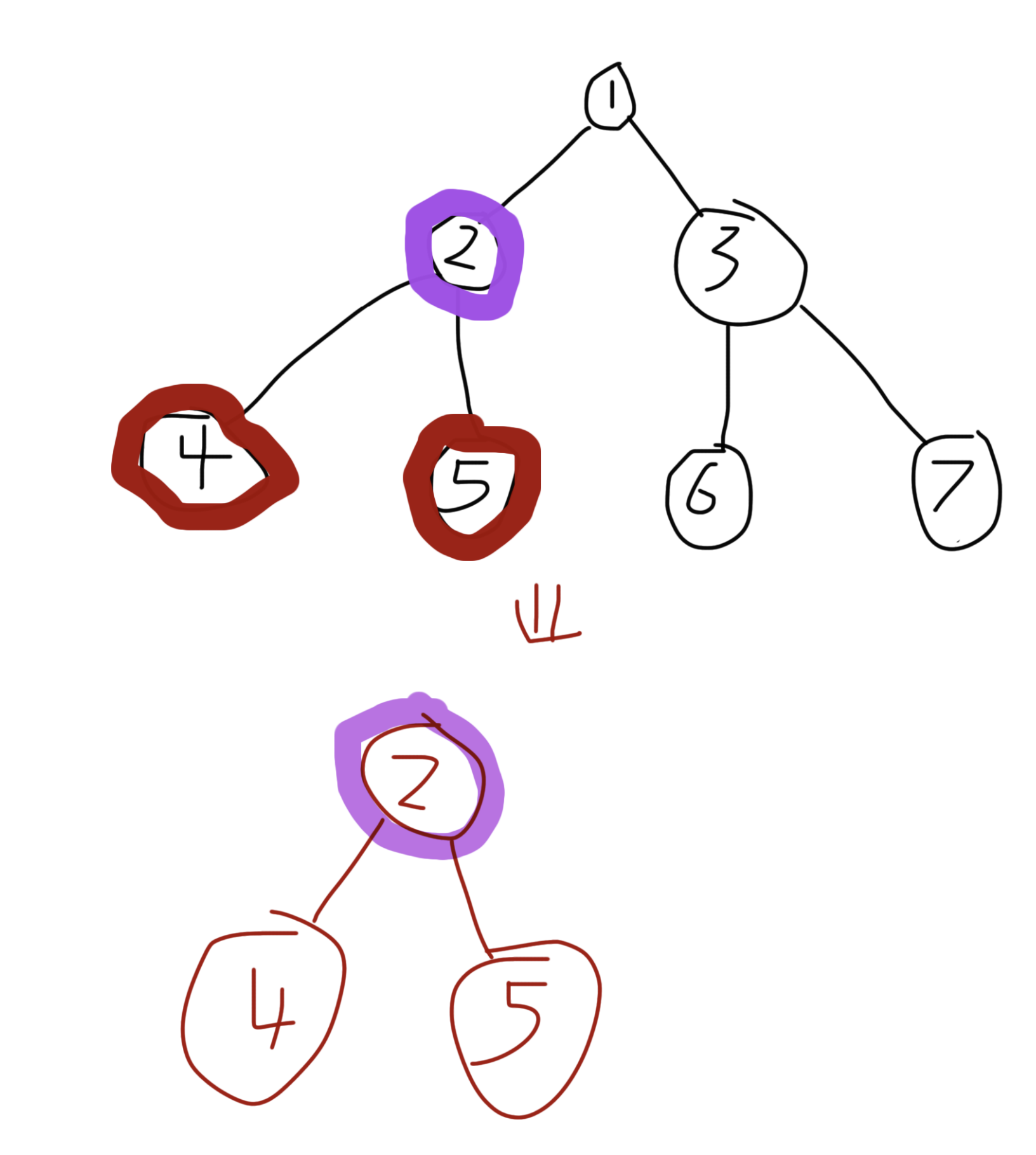
最后，把所有这些情况综合起来：
对某个分组，我们保留分组内的所有节点及它们两两路径上的所有 LCA，删去其他与之无关的节点与边，并对路径中连续的边进行压缩，就得到了一棵新的树，这棵树就是这组节点对应的「虚树」。

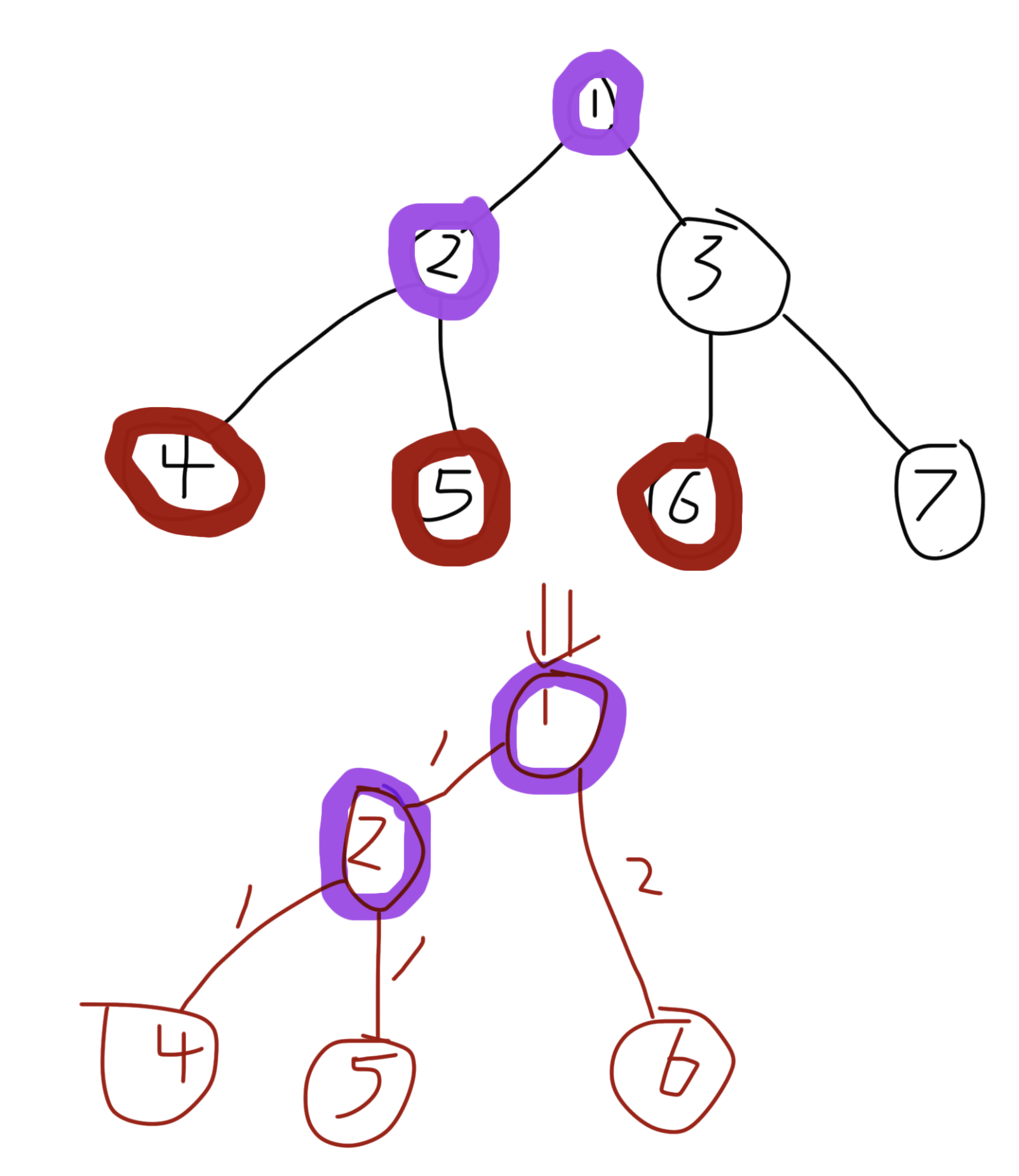
所以，可以把虚树理解为：在一棵大树上，围绕某个分组节点，将与其相关的结构抽取出来并压缩后形成的一棵小树。

在虚树上，我们依然可以使用前面提到的「边的贡献法」来计算答案。
唯一的区别是：每条虚树边都带有一个权重 d，表示它在原树中对应了 d 条边，因此这条边对答案的贡献需要再乘上权重 d。

ll ans = 0;
int Dfs(const int u, const int p, const ll groupAllNum) {
  ll uNum = 1;
  for (auto [v, d] : VirtualTree::vg[u]) {
    if (v == p) continue;
    int vNum = Dfs(v, u, groupAllNum);
    ans += vNum * (groupAllNum - vNum) * d;
    uNum += vNum;
  }
  return uNum;
}

假设某个分组中有 k 个节点，可以证明：在把所有必要的 LCA 节点加入虚树之后，虚树上的节点数不会超过 2k-1，因此构造一棵虚树的复杂度是 O(k) 级别的。
对所有分组综合起来，整体复杂度仍然是 O(n) 量级。

三、虚树的构造

从上一小节可以看出，只要能基于每个分组构造出对应的虚树，整道题就可以在 O(n) 复杂度内解决。
接下来，我们来看看如何高效地构造虚树。

分组中的节点本身很容易收集到，关键难点在于：如何找到所有需要加入的 LCA。
如果暴力对分组内所有点对求 LCA，复杂度是 O(k^2)，在最坏情况下就会退化为 O(n^2)，显然不可接受。

观察树的结构可以发现，其实只需要求「相邻节点」的 LCA 即可。
这里的相邻节点，指的是在整棵树的 DFS 序中相邻的那些分组节点。

要做到这一点，我们先对原树进行一遍 DFS，得到每个节点的 DFS 序号 dfn[u]：

void BuildDfn(const int u, const int p) {
  dfn[u] = vTimeStamp;
  timeSeq[vTimeStamp] = u;
  vTimeStamp++;
  st[0][u] = p;
  for (int v : g[u]) {
    if (v == p) continue;
    dep[v] = dep[u] + 1;
    BuildDfn(v, u);
  }
}

LCA 的求法在前文中已经详细介绍过，这里给出一个常见的倍增实现，供参考：

int Lca(int u, int v) {
  if (dep[u] < dep[v]) {
    swap(u, v);
  }
  u = UptoDep(u, dep[v]);
  if (u == v) {
    return u;
  }
  for (int i = maxLog - 1; i >= 0; i--) {
    if (st[i][u] != st[i][v]) {
      u = st[i][u];
      v = st[i][v];
    }
  }
  return st[0][u];
}

接下来，我们把某个分组内的所有节点按 DFS 序排序，相邻两点依次求 LCA，并把这些 LCA 加入候选集合。
再将这些节点与 LCA 一起按 DFS 序排序，并在其中按顺序连接相邻节点，就可以得到虚树的边。

还有一个细节：两个节点之间如果存在多条连续的边，我们希望在虚树上用一条带权边来表示。
结合前面对虚树定义的讨论可以发现，压缩的其实总是「某个节点与其某个祖先节点之间的路径」，因此这条边的权重就是这两个节点之间的深度差。

for (int i = 1; i < m; i++) {
  int u = nodes[i], v = nodes[i - 1];
  Add(u, 1);
  Add(v, 1);
  Add(Lca(u, v), 0);
}
sort(A.begin(), A.end(), [&](int u, int v) { return dfn[u] < dfn[v]; });
m = A.size();
for (int i = 1; i < m; i++) {
  int v = A[i - 1], u = A[i];
  int lca = Lca(u, v);
  int d = dep[u] - dep[lca];
  vg[lca].push_back({u, d});
  vg[u].push_back({lca, d});
}

四、最后

凡是涉及「在树上对若干分组分别计算答案」的问题，通常都可以考虑用虚树来做一层压缩，从而把整体复杂度降到 O(n) 左右。
因此，非常建议在打 OI 比赛前，把虚树这一技巧好好掌握并多多练习。

《完》

-EOF-

本文公众号：天空的代码世界
个人微信号：tiankonguse
公众号 ID：tiankonguse-code